isicad: Параболический ли купол Исаакиевского собора?

От редакции isicad.ru: Виктор Геннадьевич Чебыкин в 1974 году окончил Уральский политехнический институт. Инженер-металлург. Его общий инженерный стаж – 38 лет, в том числе, конструкторский – 19. С 2013 года на пенсии.

Огромный опыт, широкая компетенция и творческий характер дают возможность В.Г. Чебыкину передать много полезного нынешним, в том числе, молодым инженерам и разработчикам. В научно-технических журналах им опубликовано 15 статей, в числе которых написанные в оригинальном жанре геометрических очерков-миниатюр. Несколько таких миниатюр связано с именем Габриэля Ламе, французского математика, механика, физика и инженера, 220 лет со дня рождения которого исполняется 22 июля этого года. Сегодня, с любезного разрешения автора, мы публикуем некоторые из этих очерков.

Согласно справке из Википедии, Габрие́ль Ламе́ (фр. Gabriel Lamé; 1795 —1870) — член Парижской и Петербургской академий, в 1820—1832 работал в Институте корпуса инженеров путей сообщения в Петербурге. Основные труды по математической физике и теории упругости. Разработал (1833) общую теорию криволинейных координат, ввёл (1859) т. н. коэффициенты Ламе и специальный класс функций (1839, функции Ламе). Также в честь него названы параметры Ламе в теории упругости.

I. Параболический ли купол Исаакиевского собора?

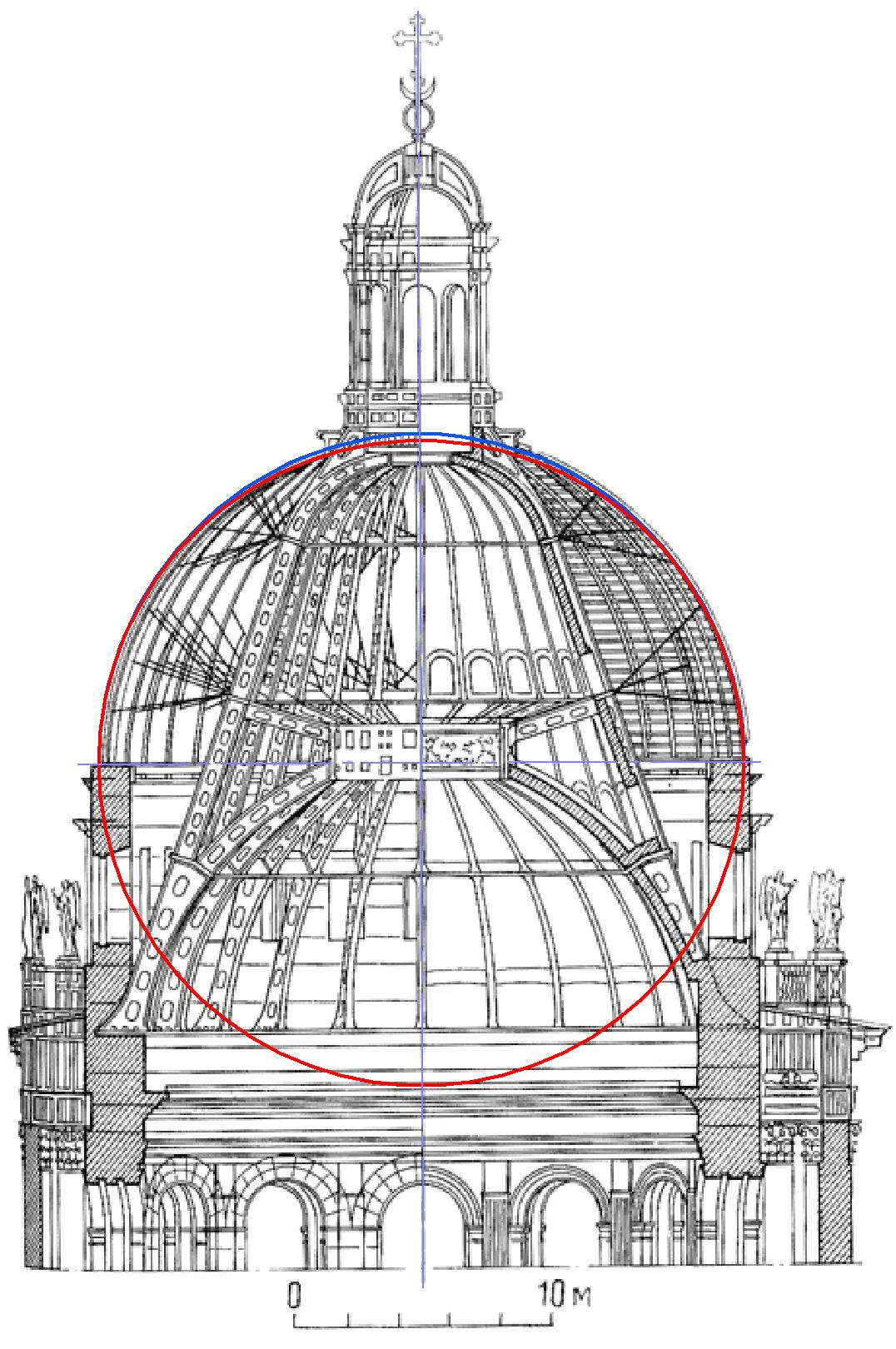
В 1820 году Габриель Ламе прибыл в Россию по приглашению для осуществления преподавательской деятельности. Кроме преподавания его, как известного инженера и математика, также привлекли к проектированию железных дорог, мостов, и … расчетам купола Исаакиевского собора. Каков был состав группы по проектированию купола мне неизвестно, но руководил ей, надо полагать, главный архитектор сооружения Огюст Монферран.

Из многочисленных литературных источников можно было почерпнуть сведения о конструкции купола Исаакиевского собора, в частности то, что состоит он из трех куполов: внутреннего – близкого к сферическому; среднего – конусного; и наружного – параболического.

Разрабатывая ранее так называемые «резервуарные» овалы, мне пришлось изучить поглубже (не просто знать формулу) кривые Ламе. В частности было замечено, что при определенных значениях степеней в формуле, кривая приобретала свойства параболы. Не потому ли купол у собора получился параболическим, что над ним работал и Габриель Ламе?

Загорелось проверить эту версию, уловить степень участия Ламе в проекте, да и просто поближе познакомиться с конструкцией купола. Тем более что над конструкцией куполов мне приходилось работать (купола резервуаров), но не будем «путать свою шерсть с общественной».

В интернете разыскал чертеж купола собора, построил нужную (параболическую) кривую Ламе, отмасштабировал ее до масштаба чертежа и вставил в нужное место. Геометрия оказалась совсем не та, что на чертеже. Пытался вписать в контур и другие параболы, менял расположение осей парабол – все безуспешно. По мере наложения на контур разных кривых выяснил, что наиболее близкую форму имеет эллипс с соотношением осей 1,02 (на чертеже не показан) и кривая Ламе с тем же соотношением осей и степенями, равными 1,98 (синяя линия). То, что это не сфера, доказывает окружность (красного цвета). Хотя показанная кривая Ламе несколько ближе к контуру купола, чем эллипс, не думаю, что Ламе добился уступки 0,02 в степенях от эллипса для того, чтобы засвидетельствовать факт применения своей кривой. Возможно это все-таки эллипс, но вкралась погрешность чертежа или его копий.

В любом случае, учитывая тот факт, что эллипс - одна из форм кривой Ламе, и то, что Ламе поучаствовал в создании собора, честь ему и хвала! Это лепесток цветка из всего букета его таланта!

P.S. Позднее я усомнился не только в параболичности купола, но и в том, что он является эллипсоидом или гипоэллипсоидом Ламе, поэтому решил ещё раз посмотреть литературу по этому вопросу. В интернете нашёл книгу Толмачевой Н.И. «Исаакиевский собор», год издания 2003, где на стр. 30-33 говорится о параболической форме третьего (внешнего) свода, а на стр. 34 читаю: «Центральный купол собора имеет сферическую форму. Это придает кафедральному храму не только спокойно-величавый силуэт, но и …». Автор книги, получается, противоречит сама себе. Ну а купол всё-таки, скорее всего – сферический, несмотря на мои измерения, наложения и предположения».

II. Овалы и их применение в инженерной практике

Эта заметка под названием «А не замахнуться ли нам на Габриеля нашего Ламе?» была впервые опубликована в журнале «САПР и графика», N8, 2013.

Как известно, овалы (франц., единственное число ovale, от лат. ovum – яйцо) – это замкнутые выпуклые плоские кривые; при этом, под выпуклостью понимают свойство кривой иметь с любой прямой не более двух (действительных) общих точек. Ниже, на рис. 1 изображены шесть овальных кривых, на первый взгляд, очень похожих между собой (за исключением 1е), но, на самом деле, обладающих разными специфическими свойствами, которые оказываются решающими в ряде важным промышленных применений. Первые три кривые (а, б, в) относятся к видам овалов, которые можно назвать классическими; остальные (г, д, е) были введены автором данной заметки для решения некоторых практических инженерных задач.

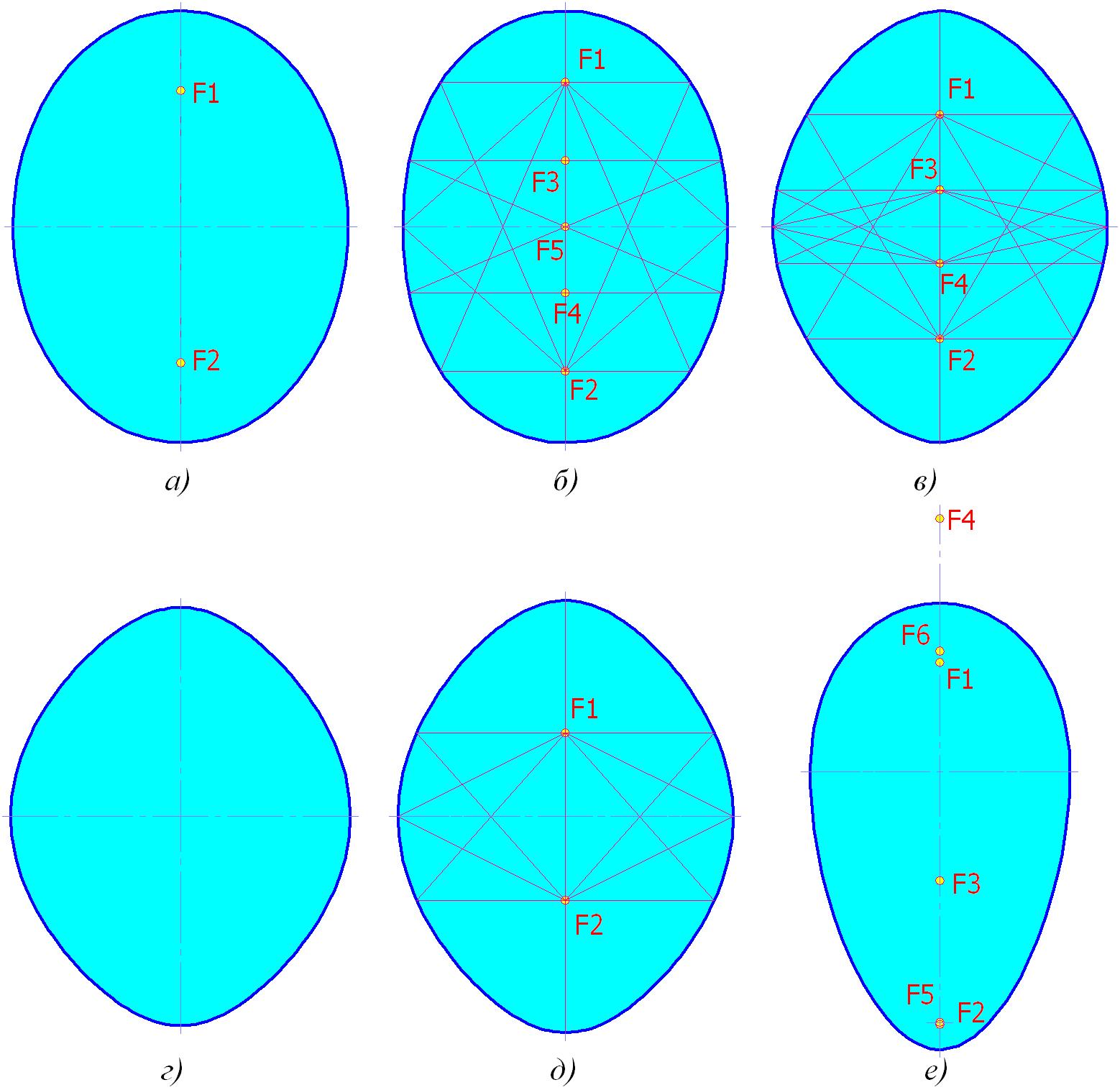
Рис. 1

Эллипс

Эту кривую (рис. 1а) знают практически все. Первые упоминания о нем датируются несколькими веками до н. э. Главные свойства эллипса: кривая имеет два фокуса; все лучи, исходящие из одного фокуса, отражаясь от кривой, собираются во втором фокусе и наоборот; сумма отрезков от любой точки кривой до фокусов есть величина постоянная. Значение эллипса трудно переоценить – его геометрию и свойства использует как природа, так и человек.

Овал Кассини

Еще одну кривую (рис. 1б) предложил астроном Джованни Кассини в 17 веке. Он полагал, что именно по такой траектории движутся планеты Солнечной системы, в чем, как выяснилось, заблуждался.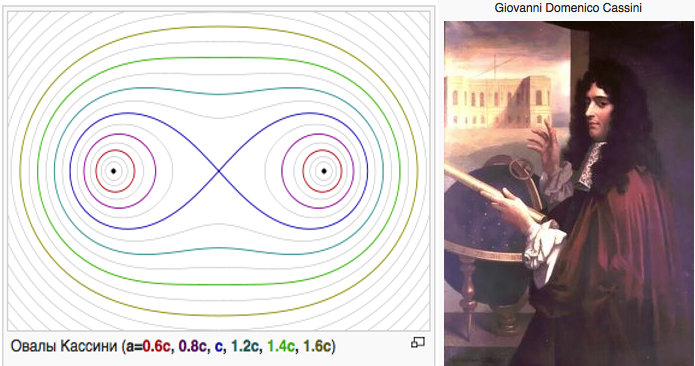

Овал Кассини – геометрическое место точек, произведение расстояний от которых до фокусов постоянно. Свойства кривой: овал Кассини не всегда имеет эллипсовидную форму и может трансформироваться в точки, совпадающими с фокусами; в два яйцевидных овала; в лемнискату; в окружность… Свойства кривой в диапазоне овалов: наличие двух основных фокусов F1 и F2, а также трех дополнительных фокусов F3, F4, F5, один из которых совпадает с центром кривой. Две пары лучей, исходящих из фокусов F3 и F4, отраженные от кривой, проходят через центр F5, и, после второго отражения от кривой, попадают в противоположные фокусы. Таких дополнительных фокусов больше нет ни у одной из описываемых в статье кривых.

Известно использование овалов Кассини в теории упругости, в конструкциях антенн, установлено геометрическое подобие овалов с формой силовых линий некоторых электромагнитных полей…

Кривая Ламе

Изображена выше на рис. 1в. Предложена Габриелем Ламе.

Формула этой кривой, иногда называемой суперэллипсом:

Формула на вид проста, но при изменении параметров, кривая может кардинально менять свою форму (рассматриваем только эллипсовидные формы овала). В отличие от овала Кассини, кривая всегда непрерывна. Еще одно свойство кривой: при разных сочетаниях m, n, a, b она может иметь два фокуса, четыре, или не иметь их вообще. Это свойство наблюдалось в диапазоне значений степеней n и m от 1,5 до 2.

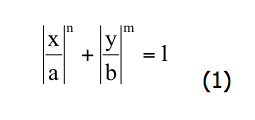
Кривая Ламе (суперэллипс) широко используется, например, в архитектуре (см. рисунок ниже), в дизайне мебели и др.

Знаменитые суперэллипсы: стадион Ацтека в Мехико и площадь в Стокгольме

Следующие три овальные кривые не входят в линейку известных, но, поскольку имеют явное практическое значение (применение) и ряд собственных характерных свойств, так же заслуживают упоминания (кривая R-0) или описания и сравнения с известными (кривые R-1 и R-2). Геометрия кривых определена с помощью 3-мерных сборок: обечайка-люк, выполненных в КОМПАС-3D.

Кривая R-0

Овальная кривая R-0 (рис. 1г) получена в результате развёртывания на плоскость фигуры пересечения поверхностей двух круглых цилиндров. Поскольку применимость ее незначительна, ограничимся лишь определением: плоская гладкая замкнутая эллипсовидная бесфокусная овальная кривая.

Кривая R-1 (резервуарный овал 1 рода)

Кривая R-1 (рис. 1д и рис. 2 ниже) впервые предложена и описана автором в статье «Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых – «резервуарные» овалы. Справочник. Инженерный журнал. 2012. № 11. С. 31-33».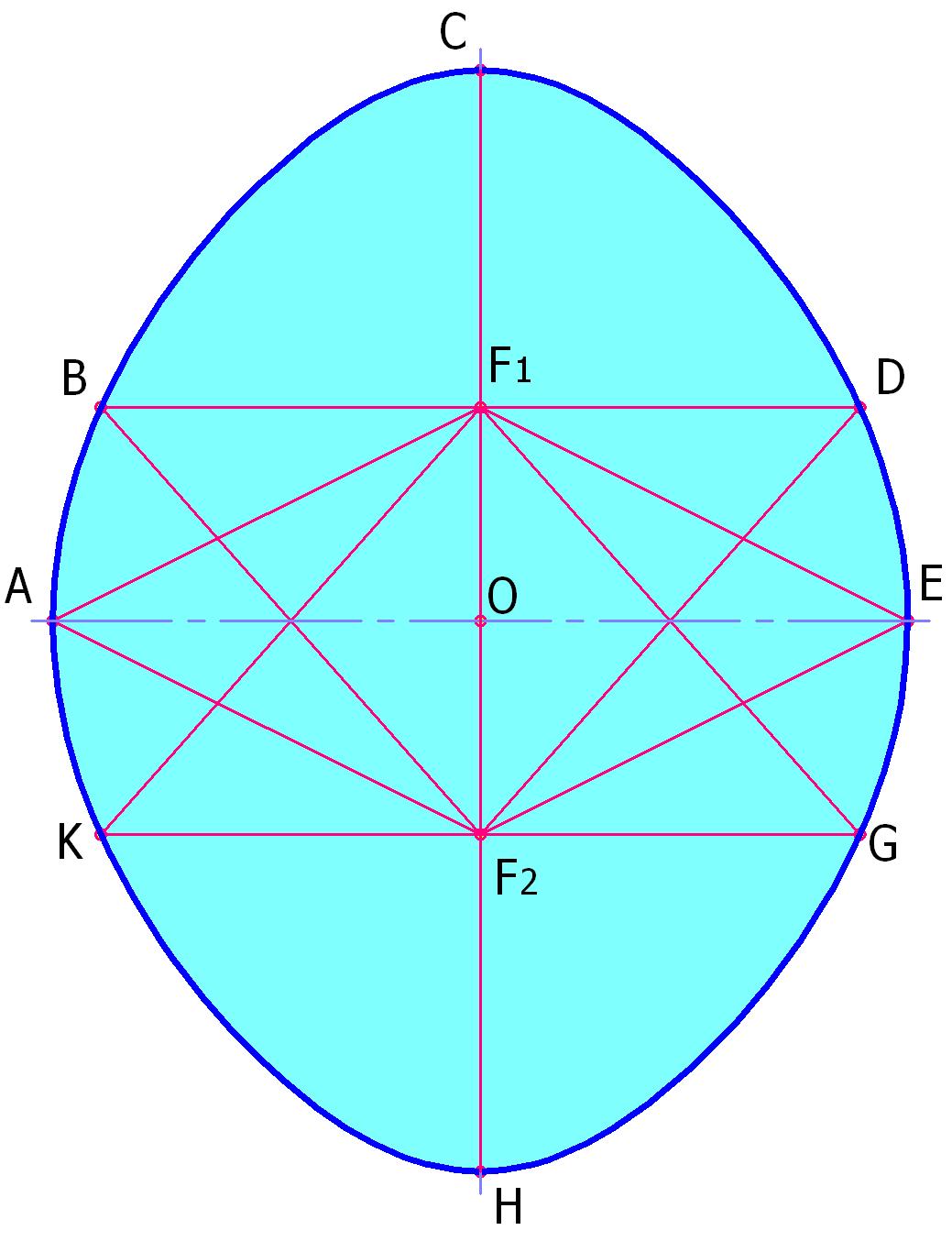

Рис. 2

Это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая. Она получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой толщиной S>0, с учетом гарантированного зазора и определяет геометрию отверстия в обечайке. Люк установлен перпендикулярно продольной оси резервуара без смещения от нее. Большая схожесть кривой R-1 с кривой Ламе (рис. 1в) не случайна. Автор пытался подогнать кривую Ламе к кривой R-1 методом последовательного приближения. Попытка не удалась – кривые не сходились, кроме того, имели разное количество фокусов. Вывод: кривая R-1 не является частным случаем кривой Ламе.

Одним из важных свойств овальных кривых R-1 является наличие двух (и только двух) фокусов во всем возможном диапазоне сочетаний параметров: диаметр обечайки – диаметр люка – толщина обечайки – гарантированный зазор. «Гуттаперчевая» кривая Ламе таким свойством не обладает, обращаясь с фокусами более вольно.

Фокусы кривой R-1 могут обменяться между собой восемью парами лучей, отраженных от кривой и парой прямых лучей. У эллипса, как известно, все лучи от одного фокуса собираются в противоположном.

Овал R-1 обладает еще одним свойством: вышеупомянутые лучи делят кривую овала на 8 частей. Точки падения этих лучей на кривую являются характерными точками, в которых меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный (см. рис. 2). Интервалы кривой с положительными и отрицательными знаками чередуются. У эллипса, как известно, сумма отрезков от любой точки контура до фокусов есть величина постоянная.

Ниже приведены формулы для определения большой и малой осей этой овальной кривой (все формулы в статье выведены автором):

Кривая R-2 (резервуарный овал 2 рода)

Эта кривая (рис. 1е и ниже — рис.3, рис. 4) также предложена и описана в моей вышеупомянутой статье в «Инженерном журнале».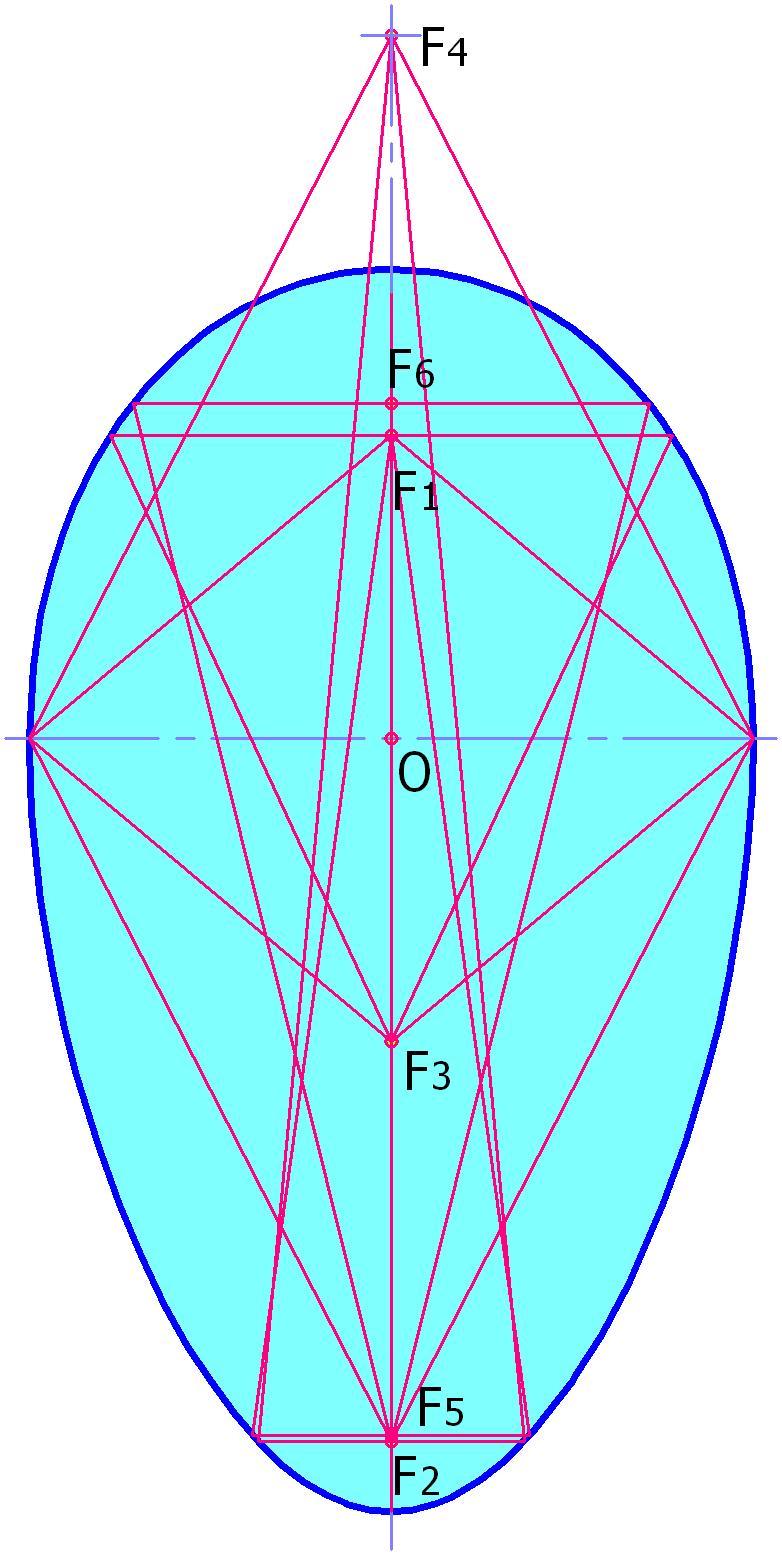

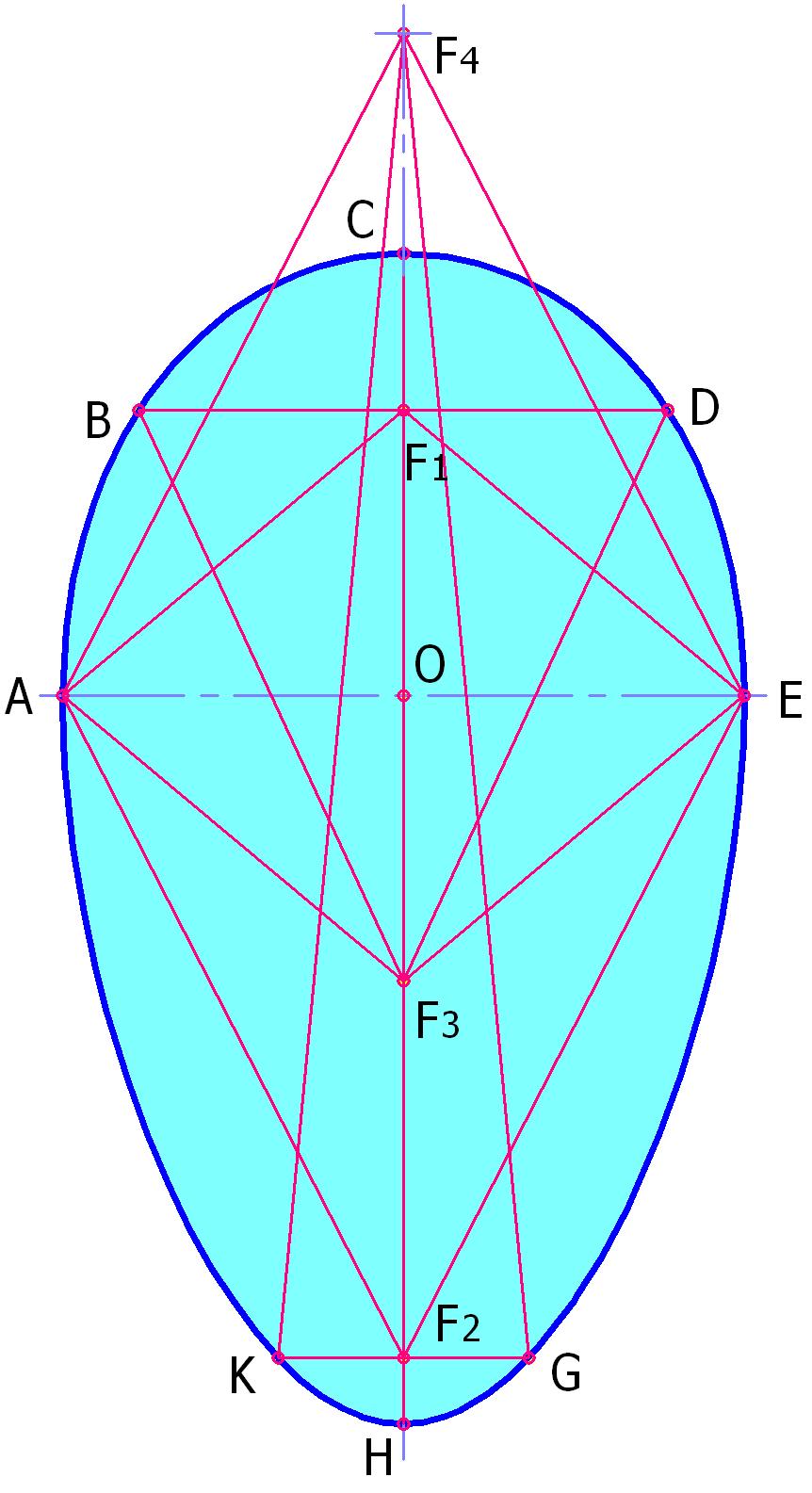
Рис. 3 и Рис. 4

R-2 — плоская замкнутая яйцевидная шестифокусная овальная кривая. Она получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой резервуара с толщиной стенки S>0 с учетом гарантированного зазора и определяет геометрию отверстия в обечайке. Ось люка перпендикулярна продольной оси резервуара. Люк установлен со смещением от этой оси.

Овал R-2 имеет яйцевидную форму. Его характерным свойством является наличие шести фокусов (см. рис. 3). Шесть лучей, выпущенные из фокуса F1, отраженные от кривой, собираются в противоположном ему фокусе F3 и наоборот, фокусы F2 и F4 связаны между собой пятью парами отраженных лучей, пары фокусов F1 - F5 и F2 – F6 могут обменяться между собой только четырьмя парами отраженных лучей.

Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F2 не постоянна и растет по мере отдаления от полюса H к полюсу C (см. рис. 4). Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F3 не постоянна и имеет смену знака роста в характерных точках A, B, С D, E, H. Сумма отрезков, соединяющих точки на кривой с фокусами F2 и F4 также не постоянна и имеет смену знака роста в точках A, C, E, G, H, K.

Еще одно свойство: точки A и E являются точками перелома кривой, в связи с чем, кривая не относится к гладким.

Указанными свойствами кривая отличается как от R-1, так и от эллипса.

Размеры осей овальной кривой R-2 можно определить по формулам:

Проверка геометрии полученных кривых в 3D-моделлере выполнялась следующим образом. На 3D-модели обечайки в развернутом состоянии вырезали по полученной кривой отверстие, после чего обечайку сворачивали в круговой цилиндр и соединяли с моделью люка. Далее с этой 3D-сборки создавался чертеж – вид сверху, на котором проводились измерения. Результат проверки следующий – отклонение от заданного гарантированного зазора не превышало нескольких сотых миллиметра (кривая была выполнена сплайном по 40 точкам). При увеличении количества опорных точек точность построения возрастает.

Предложенные автором кривые были проверены и непосредственно при разработке и изготовлении резервуаров, где они показали свою состоятельность. С использованием овальных кривых R-1 и R-2 изготовлены уже несколько сотен резервуаров, при этом, ни одного случая плохой стыковки обечайки с люком не зафиксировано, что окончательно доказывает правильность их геометрии. На рис. 5 показан один из резервуаров, конструкция которого выполнена с использованием кривой R-1.

Рис. 5

Результатом работы, изложенной в данной заметке, является расширение линейки известных овальных кривых: предложены и описаны «резервуарные» овалы 1 и 2 рода (овальные кривые R-1 и R-2), назначение которых определяется объединяющим их термином.

III. Кривая Ламе – геометрический хамелеон

В первых двух частях данной публикации уже были отмечены важные и интересные работы Габриэля Ламе – в том числе, была представлена кривая Ламе. В этой заметке я покажу, насколько многообразны воплощения этой кривой при задании тех или иных её конкретных параметров.

Известно, что кривая Ламе при степенях 0,5 и равных между собой осях имеет форму четырёхконечной звезды с вогнутыми параболическими сторонами (рис. 1б). Но таких параболических звёзд при желании можно построить множество и форма их будет зависеть от отношения радиуса вершин к фокальному параметру параболы. В отличие от астроиды, также четырёхконечной равноосной звезды, эти кривые не имеют своего имени. Исправим это недоразумение и назовём их тетрапарабоидами.

Переменная тетрапарабоиды (w) – величина равная отношению радиуса вершин к фокальному параметру парабол, образующих кривую. Область изменения этой переменной: 0 < w ≤ √2.

Следует отметить, что только одна из тетрапарабоид совпадает по геометрии с кривой Ламе, та, у которой переменная w = √2. Назовем её тетрапарабоидой Ламе.

Аналогично можно поступить и с равноосной фигурой, состоящей из двух парабол (рис. 1и), назвав её бипарабоидой или бипарабоидой Ламе.

Постоянная равноосной бипарабоиды (k) =2, величина равная отношению полуоси кривой к фокальному параметру парабол, образующих кривую.

Далее по тексту будут предложены ещё несколько терминов, относящихся к диапазонам кривой Ламе.

Известны несколько кривых, меняющих свою форму при изменении параметров. Одни меняют только размеры, другие – и размеры и конфигурацию (форму). Наиболее известной в этом отношении кривой является овал Кассини, который упоминался во втором разделе данной публикации. При изменении отношения параметра с (половина расстояния между фокусами) к параметру a (произведение расстояний от фокусов до любой точки кривой) овал Кассини может иметь форму: окружности; овала; выпукло-вогнутой кривой; лемнискаты; двух яйцевидных овалов; двух точек.

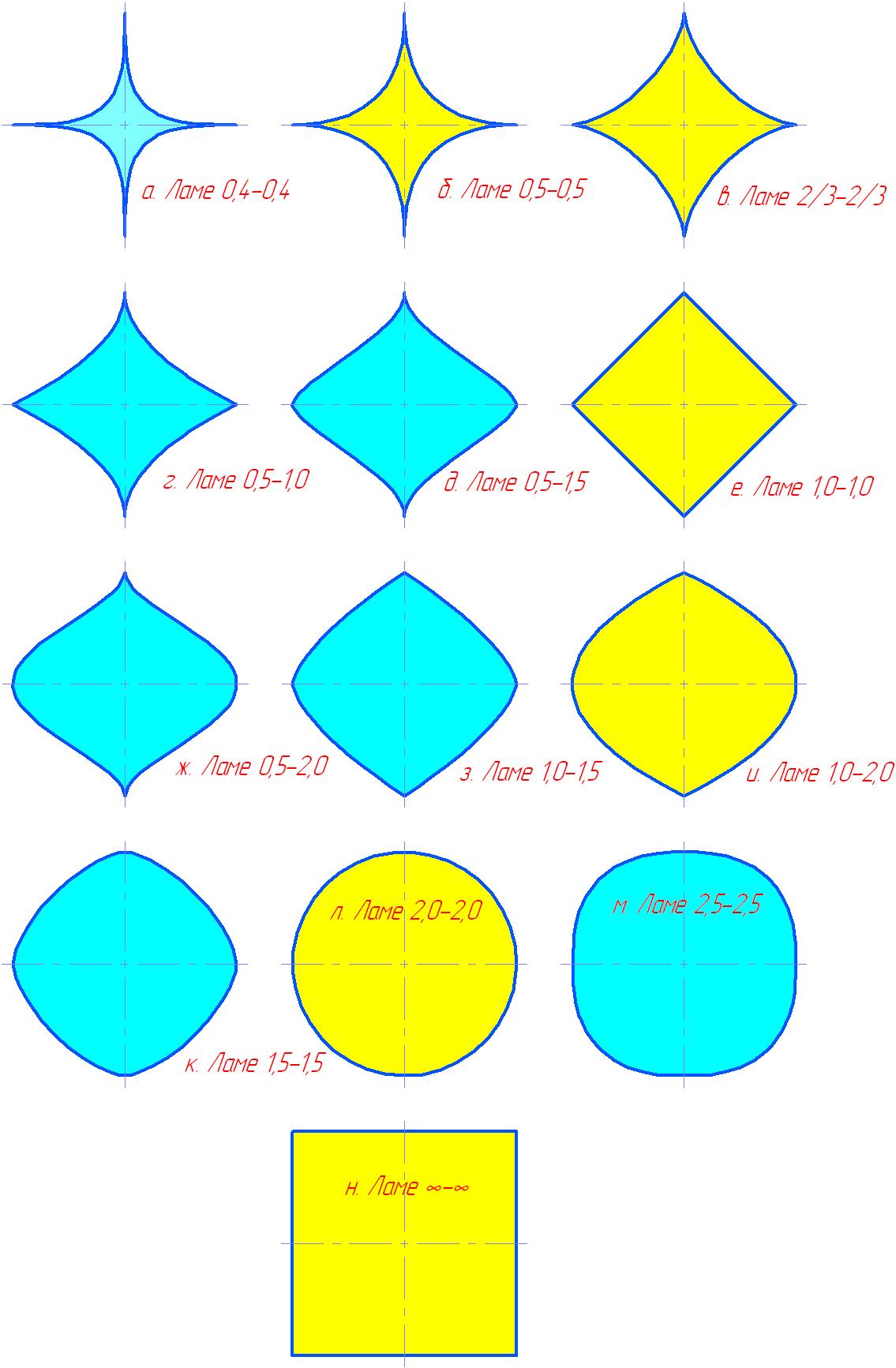
Рис. 1. Формы кривых Ламе

Кривая Ламе по способности к перевоплощению не уступает овалу Кассини, в чем можно убедиться, просматривая фигуры на приведённом выше рисунке, где изображены кривые Ламе при полуосях a=b:

1а - допараболический диапазон кривых Ламе;

1б – степени m=n=0,5 – тетрапарабоида Ламе; без рисунка – постпараболический диапазон;

1в – m=n=2/3 – астроида;

1г, 1д – постастроидный диапазон;

1е – m=n=1 – квадрат;

1ж, 1з – постквадратный диапазон;

1и – m=1, n=2 – бипарабоида Ламе;

1к – диапазон гипоокружностей;

1л – m=n=2 – окружность; 1м – диапазон гиперокружностей;

без рисунка - m>2, n<2 – диапазон гипергипоокружностей;

1н – m=n=∞ - квадрат.

Желтым цветом показаны формы кривой, когда она совпадает с другими видами кривых, синим – оригинальные формы.

Как видим, кривая Ламе по мере изменения степеней совпадает по форме с параболой и квадратом дважды, а с окружностью и астроидой по одному разу. Попытки найти совпадение кривой с окружностью в диапазоне между параболой и астроидой (диапазон степеней 1/2 - 2/3) закончились неудачей – кривые сближались, но полного совпадения их формы не случилось. Загадка?!

Диапазон кривой Ламе расширяется, если а ≠ b. Так появляются вытянутые тетра- и бипарабоиды, вытянутая астроида, ромб, эллипс, гипо-, гипер- и гипергипоэллипсы, прямоугольник, ну и вытянутые диапазонные кривые Ламе.

Ещё одно свойство кривой Ламе (касается диапазонов гипо- и гиперэллипсов) – это способность иметь разное количество фокусов при изменении параметров a, b, m и n. Об этом свойстве говорилось в предыдущем разделе этой серии заметок: благодаря этому свойству кривая Ламе была названа «гуттаперчевой» кривой.

Вот такую замечательную и загадочную кривую придумал в 1818 году Габриэль Ламе!

IV. Фокусы и другие загадки кривой Ламе

Продолжим изучение кривой Ламе, в частности, попробуем ответить на вопрос: достаточно ли полно и разносторонне используется эта замечательная кривая.

Фокусы кривой

Речь идет о фокусах в диапазонах гипо- и гиперэллипсов Ламе, о которых шла речь в предыдущих разделах данной статьи.

Фокус – термин многозначный. Вот некоторые значения этого слова из Википедии:

Фокус – точка в оптической системе;
Фокус – номер иллюзиониста, демонстрирующий необъяснимый эффект, «чудо».
Фокус кривой (или поверхности) – в геометрии: точка, для которой выполняется определённое соотношение со всеми точками кривой (поверхности). В частности, фокус конического сечения.

Факт наличия (или отсутствия) геометрических (оптических) фокусов у кривой Ламе установлен автором при разработке и исследовании «резервуарного» овала R-1 и сравнении его с другими овалами (см. выше). Овал R-1, независимо от параметров резервуара, всегда имеет два фокуса. В отличие от него, гипо- и гиперэллипсы Ламе могут иметь и два, и четыре фокуса, или не иметь их вообще (рис. 1):

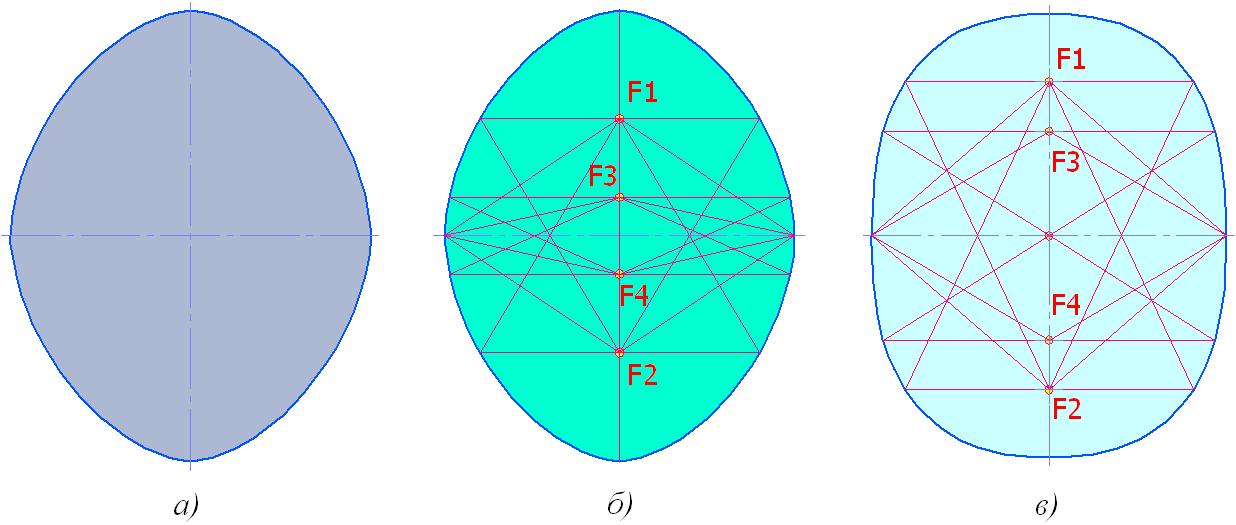
Рис.1. Гипо- и гиперэллипсы Ламе: а) гипоэллипс (бесфокусный); б) гипоэллипс (4 фокуса); в) гиперэллипс (4 фокуса)

Зная параметры кривой Ламе можно мысленно представить её форму, а вот число фокусов и их расположение можно определить только после построения. И пока не будут выяснены причины и условия появления и исчезновения этих фокусов (по крайней мере, мне это не удалось сделать), кривую Ламе можно считать «иллюзионистом», демонстрирующим необъяснимое. Так что, пока это – предмет для дальнейшего изучения.

ЛАбиринт ЛАме

Ещё одно из малоизученных свойств этой кривой касается обтекаемости гипоэллипсоидов (понятно, что гиперэллипсоиды им здесь не конкуренты). Это уже аэродинамика (гидродинамика), в которых обтекаемость — одна из самых важных характеристик. А кривая Ламе, как выясняется, обладает очень неплохими указанными свойствами, благодаря которым появляется возможность её нового применения.

Можно ли визуально оценить обтекаемость того или иного тела вращения? Можно, если сравнивать тела с существенной разницей в геометрии. А выбрать наиболее обтекаемую форму из близких и похожих? Думаю, что это маловероятно. Сможет ли кто-нибудь назвать степени в формуле Ламе, благодаря которым гипоэллипсоид будет самым обтекаемым?

Я этого не смог сделать, поэтому решил, кроме создания 3D-моделей гипоэллипсоидов, ещё и посчитать их лобовое сопротивление давления (ЛСД). Хотя это сопротивление является частью полного сопротивления движущегося тела в воздушной или водной среде, для предварительной оценки обтекаемости оно может быть достаточным. Для получения более точных расчетов ЛСД лобовая часть моделей делилась на 12 частей. ЛСД головной части из-за большой кривизны считалось отдельно.

Создаваемые модели гипоэллипсоидов, разумеется, имели одинаковые длину и площадь миделя. Соотношение осей a/b=2π выбрано произвольно

Поскольку определить оптимальные степени для обтекаемости сразу не удалось, стало понятно, что наскоком эту задачу не решить и надо быть готовым к затяжному, слегка нудному, но в тоже время интересному поиску.

Для начала создал таблицу (рабочее название – «поляна гипоэллипсоидов Ламе»), предназначенную для записи значений ЛСД (рис. 2):

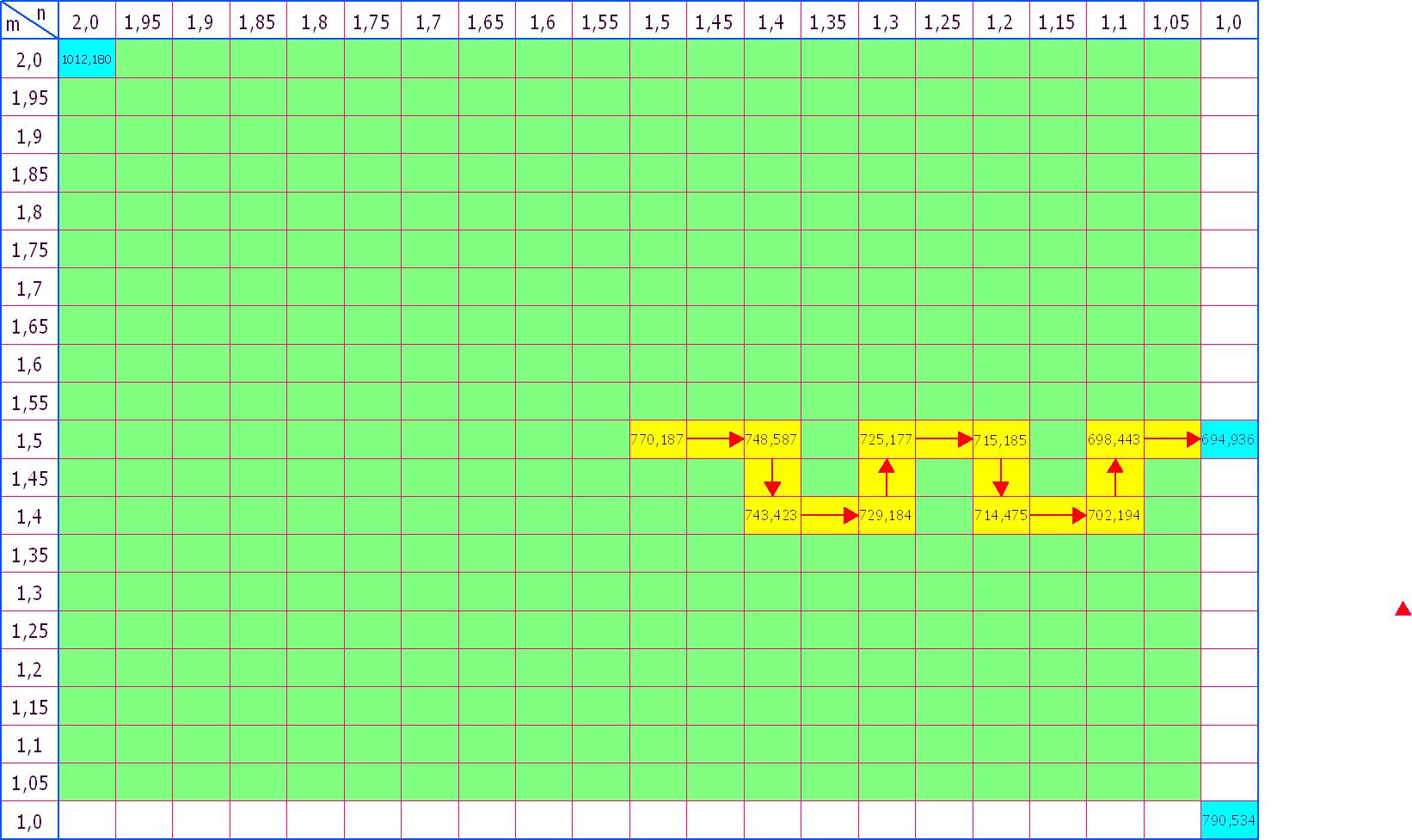
Рис. 2. Поляна гипоэллипсоидов Ламе

Сочетание степеней в формуле кривой вначале выбирал произвольно, вразброс, как это делается в известной игре «Морской бой». В ходе поиска постепенно вырисовывалась «область залегания» наиболее обтекаемых гипоэллипсоидов, поэтому выбор сочетания степеней стал более прицельным. Линейка гипоэллипсоидов по убыванию ЛСД, которая прогнозировалась как прямая линия, оказалась зигзагообразной и названа «Лабиринтом Ламе» (на рисунке выделена желтым цветом). Оригинальная закономерность, которую трудно было бы предугадать, не правда ли?

На рис. 3 изображена 3D-модель одного из гипоэллипсоидов «Лабиринта»:

Рис. 3. Гипоэллипсоид Ламе (m=n=1,5; a/b=2π)

Всего было создано и обсчитано (ЛСД) около тридцати моделей гипоэллипсоидов и, надо сказать, потрачено на это немалое количество времени, но общей картины «поляны Ламе» они всё-таки не дают. Для этого надо заполнять таблицу до конца. Хорошо бы автоматизировать процесс создания моделей и расчет ЛСД. Возьмется ли за это кто-либо, например Ледас? Ведь смогут, если захотят…!

В 2018 году кривой Ламе будет 200 лет, а белые пятна в её изучении всё ещё есть, да и опциональные возможности далеко не исчерпаны.