isicad: А теперь… Кассини!

Корней так много квадратных
На улице Кассиньевой...
По мотивам стихотворения Н. Доризо

Овал Кассини и Википедия

При подготовке заметки «Метод акульих зубов» смотрел статью «Овал Кассини» в Википедии и заметил там ошибку: «В уравнении кривой содержатся два независимых параметра:

c

— половина расстояния между фокусами и

a

— произведение расстояний от фокусов до любой точки кривой».

Решил попробовать исправить текст, и, после нескольких попыток, это удалось сделать: «В уравнении кривой содержатся два независимых параметра: $c$ — половина расстояния между фокусами и $a$ — корень квадратный из произведения расстояний от фокусов до любой точки кривой».

После этого посмотрел, отразилась ли правка в иноязычных версиях. Оказалось, что нет и, более того, последние правки в них были различными по содержанию и датам. При сравнении версий выяснил также, что и сама статья в версиях различна по объёму и содержанию. К примеру, формулам, приведённым в одних версиях, «не нашлось места» в других. Это удивило и привело к выводу (правильному ли?): версии существуют независимо друг от друга и никто их не «равняет» между собой. Ещё заставило улыбнуться название овала Кассини на словенском языке: Cassinijeva jajčnica. Вот такой экскурс в Википедию был мной совершён.

Хотел также сделать дополнение в статью по оптическим свойствам овала Кассини, но, прочитав «Условия использования», понял, что без ссылки на авторитетный источник оно вряд ли прошло бы. Потому и задумана была данная статья.

Знаковые числа и оптические фокусы овала Кассини

Известными знаковыми числами овала являются соотношения его параметров «a» и «c»: a/c = 0 (кривая вырождена в точки, совпадающие с алгебраическими фокусами); a/c = 1 (лемниската Бернулли); a/c = √2 (первый выпуклый овал); a/c = ∞ (овал вырождается в окружность). В промежутках между этими формами овала находятся: диапазон пар яйцевидных овалов; диапазон выпукло-вогнутых овалов и диапазон выпуклых овалов.

Однако к перечисленным знаковым числам следует добавить ещё, по меньшей мере, два: a/c = √(√2+1) (соотношение параметров «a» и «c» равно соотношению осей овала); a/c = 2 (исчезновение оптических фокусов 2 категории).

Оптические фокусы появляются при переходе от лемнискаты к выпукло-вогнутому овалу, причём все сразу, по два каждой из трёх категорий. При переходе в диапазон выпуклых овалов они сохраняются, при достижении a/c = 2 фокусы 2 категории исчезают, а фокусы 1 и 3 категории остаются вплоть до вырождения овала в окружность. На рис. 1 показан овал с соотношением параметров a/c = 1,9.

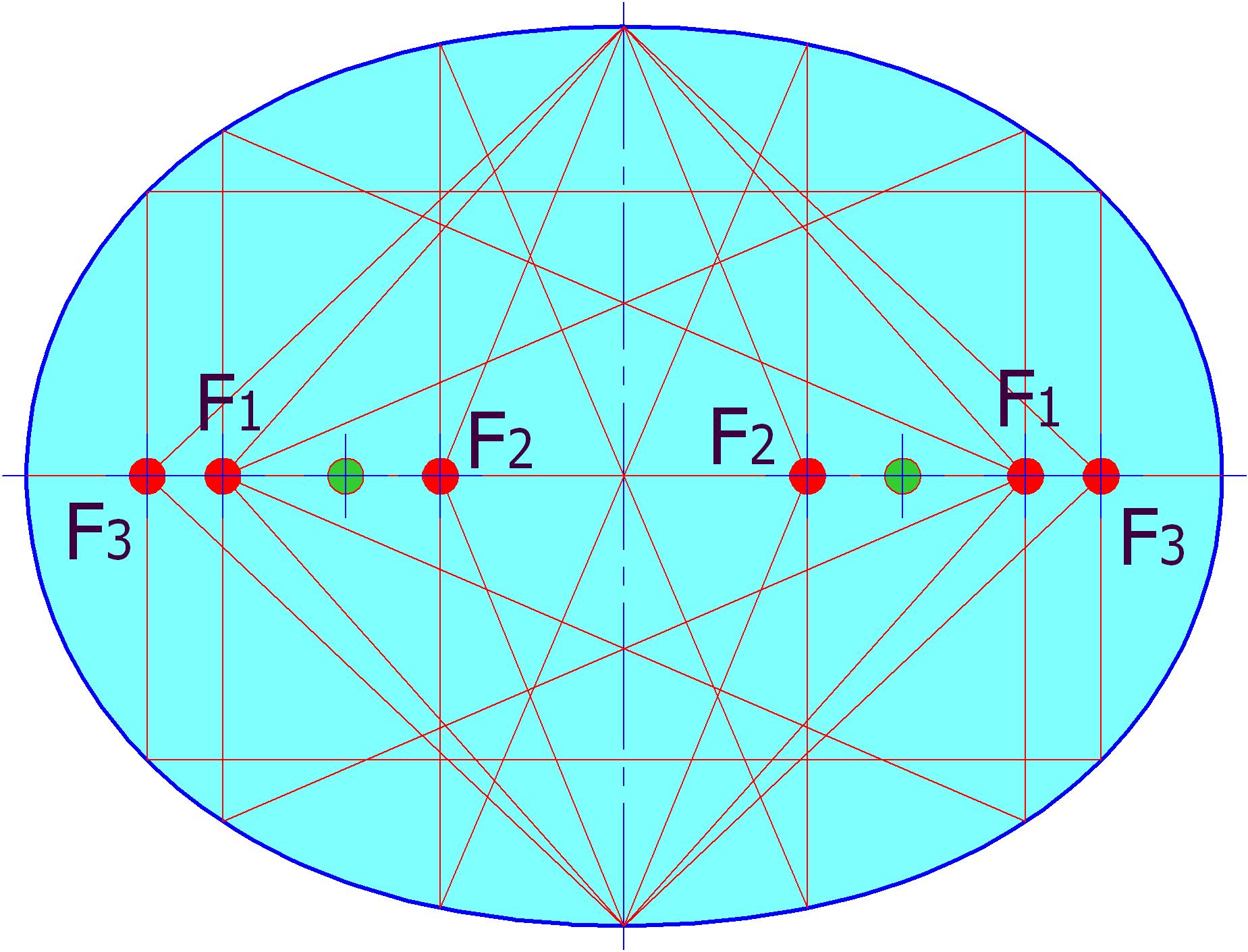
Рис. 1

Зелёным цветом показаны алгебраические фокусы, красным – оптические фокусы 1, 2, и 3 категорий (обозначены нижними индексами). О категориях оптических фокусов подробней можно узнать в статье «Метод акульих зубов».

График зависимости соотношения осей овала Кассини от соотношения его параметров

Представить форму эллипса по численным значениям длин осей несложно. Другое дело, по значениям параметров овала Кассини также представить его форму. Это несколько сложнее. Ну а если возникнет, например, такая задача: выполнить чертёж кулачка (эксцентрика) в форме овала Кассини с соотношением осей, равным, например, 2,5? Эту задачу поможет решить график m/n = f (a/c), где «m» и «n» – оси (полуоси) овала. Этот график показан на рис. 2.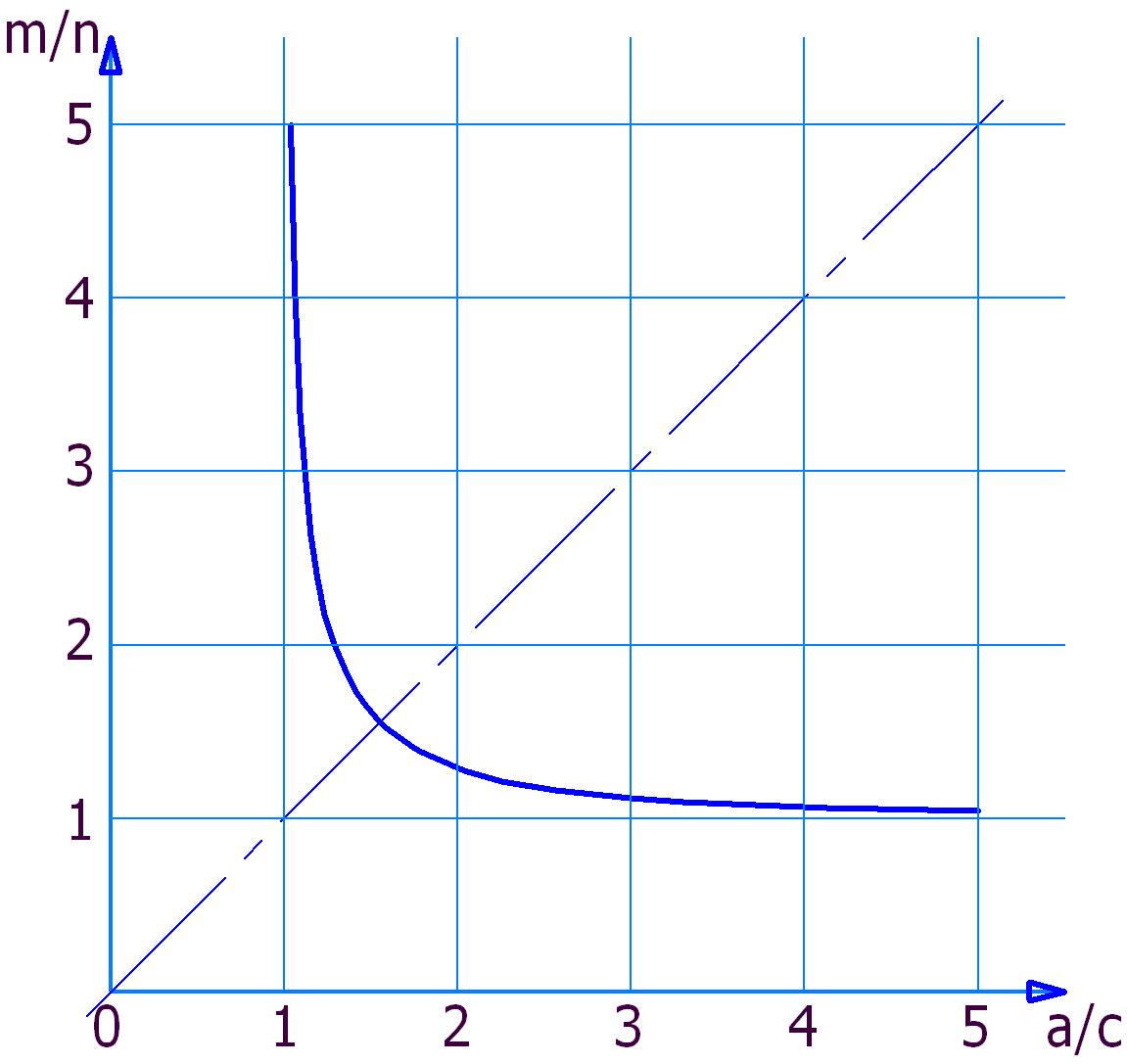

Рис. 2

Кто-нибудь скажет, что это за кривая? Для справки даю координаты вершины и двух точек кривой: вершина – ( √(√2+1) ; √(√2+1) ); 1 точка – (√2; √3); 2 точка – (√3; √2). Кстати, все точки построения кривой найдены как корни некоторых целых и дробных чисел.

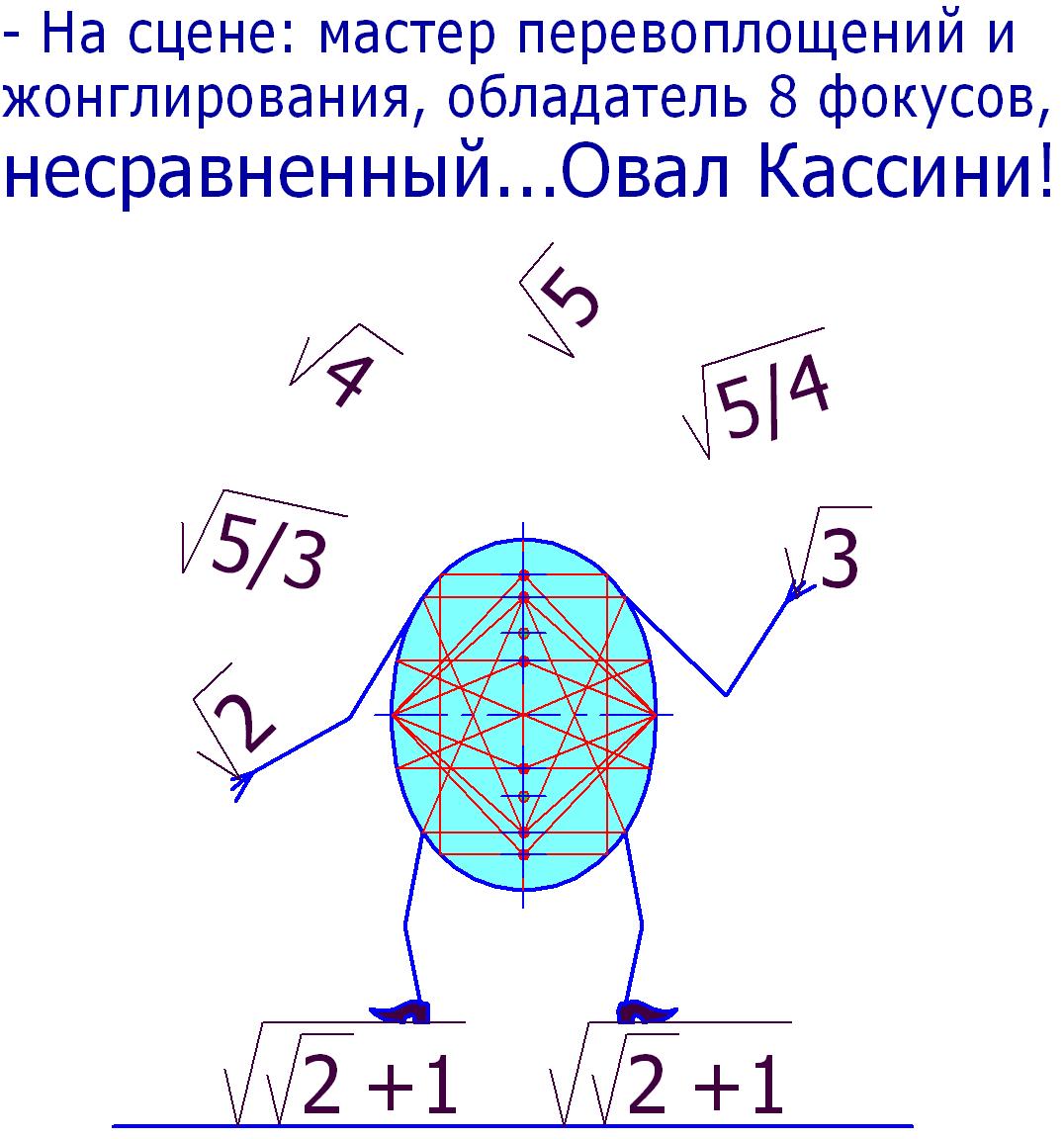
Рис. 3

P.S. Как видите, овал Кассини обладает некоторыми, не описанными в статье Википедии (и не только в ней) свойствами. Считаете ли вы, что дополнение статьи этими свойствами необходимо (желательно), или ну их…, в смысле: пусть остаётся как есть?

***

Ответ: не гипербола.
Формула кривой: y=√(((x^2+1))⁄((x^2-1) )) .
Назовём кривую «Кассиниев решатель».
Ближайшая по форме гипербола имеет формулу: xy=(√(√2 +1) -1)^2.