
Галилео Галилей в 1638 году написал в своей книге «Беседы и математические доказательства…», что цепь, висящая на двух гвоздях, принимает форму параболы. Он был уверен в этом и, возможно, поэтому не «докопался» до истины и не открыл новую кривую – цепную линию. Эту кривую 50 пет спустя описали Гюйгенс, Лейбниц и Якоб Бернулли. Они первыми вывели формулу кривой и исследовали её свойства.
На рисунке 1 изображены три кривые.
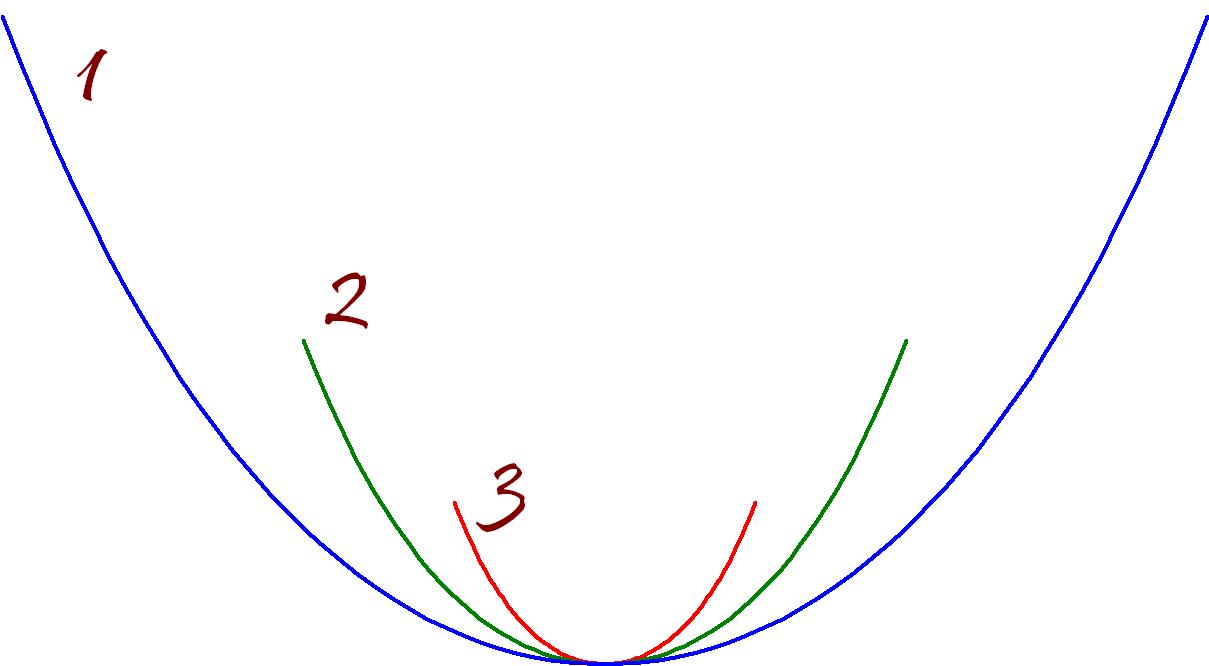
Рис. 1
На известном научно-популярном сайте «Математические этюды» в этюде «Цепная линия» рассказывается об этой кривой: «Если некоторым образом подобрать параметр в уравнении, то центр квадрата, катящегося без проскальзывания по дуге цепной линии, будет двигаться ровно по прямой!». Какую цель нужно достичь, понятно, а вот как это сделать, данная фраза если не умалчивает, то, по крайней мере, предлагает не самый рациональный путь. В чём заключается этот «подбор некоторым образом»? Ну, допустим, подобрали, и что дальше? Решать уравнение и строить кривую? А если изменится размер колеса, то снова подбирать, решать и строить? А может, эти слова означают «Суть способа не раскрывается, ноу-хау»? 
Предлагаю иной способ решения этой задачи:
- Построим по формуле Y=a chX/a цепную линию с произвольным параметром a, например, равным 10 мм (рис. 2);
- На расстоянии от вершины, равном a(√2-1), проведём горизонтальную хорду. Измерим длину дуги, стягиваемой хордой. Она должна быть равна 2a;
- Скопируем построенную кривую в новый фрагмент, отсечём отрезки, выходящие за пределы сегмента и повернём его на 180°. Этот сегмент и будет частью «дороги» для квадратного колеса;
- Построим квадрат со стороной 2a;
- Прокатывая квадрат по сегменту цепной линии, убеждаемся в отсутствии вертикальных перемещений его центра.
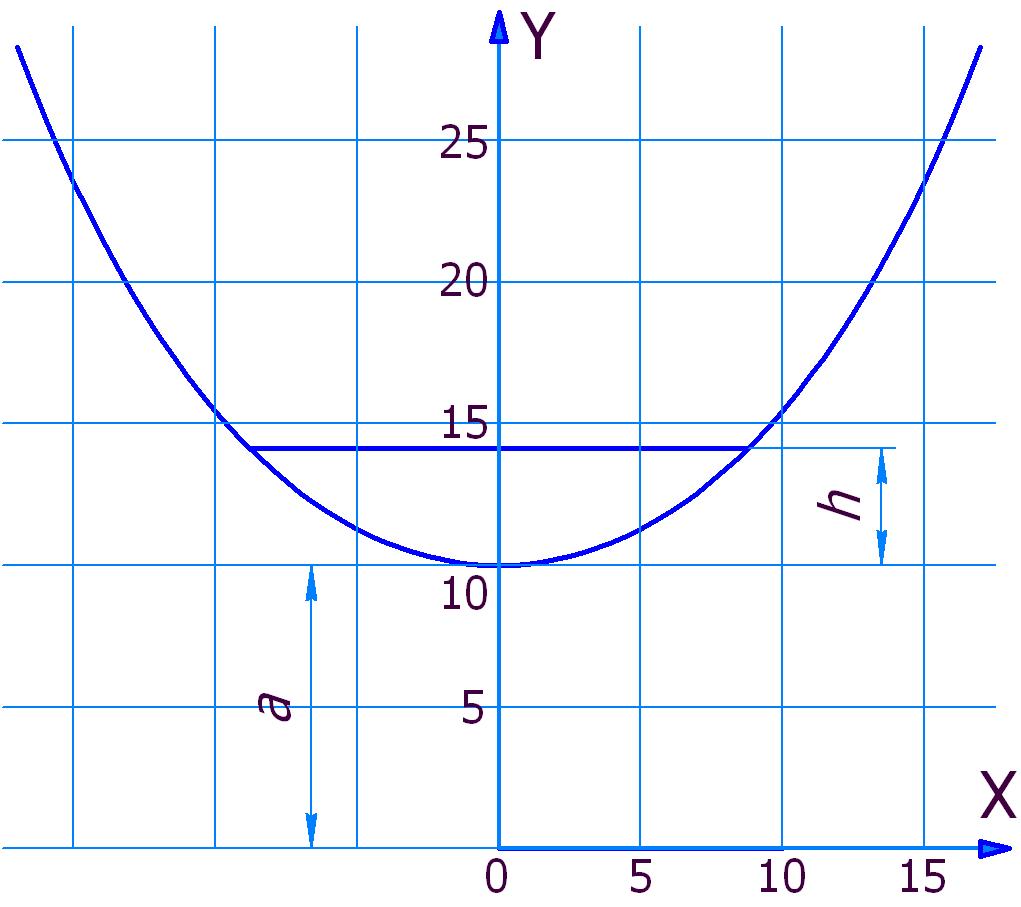
Рис.2
Кстати, кривая, показанная на рисунке 2, построена всего по 69 точкам и, не смотря на это, обладает неплохой точностью: дуга, отсекаемая хордой, имеет размер 19.9999634224 мм при расчётном размере 20 мм.
А что же с другими многоугольниками? Для всех их (кроме треугольника) можно построить собственную «брусчатку» из сегментов цепной линии, по которой они прокатятся без колебания центра. Порядок построения несколько иной, чем для квадрата: также используется ранее построенная цепная линия (рис. 2), но положение хорды определяется касательными к кривой (для шестиугольника, например, под углами 30 и -30 градусов), а размер стороны многоугольника определяется измерением дуги сегмента. Это связано с тем, что только для квадрата свойственна зависимость: сторона равна удвоенному параметру цепной линии.
Ещё было интересно посмотреть, что покажут другие кривые в качестве «брусчатки» для квадратных колёс. Были проверены: окружность, парабола, овал Кассини и несколько овалов стабильной формы. Как и ожидалось, «идеальных» больше нет. Результаты построений и расчётов взаимодействия квадратного колеса со стороной 400 мм с некоторыми кривыми сведены в таблицу 1.
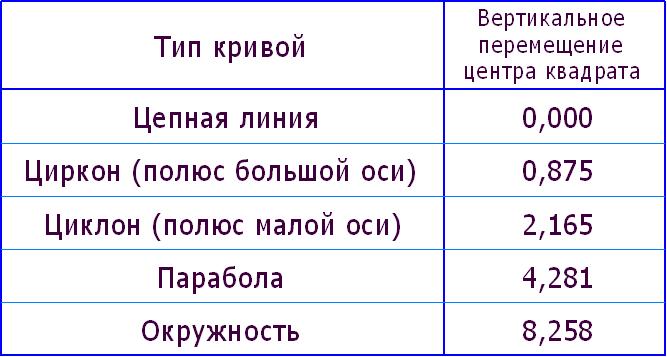
Таблица 1
 А цепная линия… – без конкуренции!
А цепная линия… – без конкуренции!
Рис. 3