Яйцевидный овал как производная

Принимая за исходную парадигму содержание эпиграфа, можно попытаться пойти дальше и, взяв за основу классические овалы – окружность и эллипс, создать новый вид кривых, как производное от классики.

Выразим алгоритм построения новой кривой в общем виде: берём за базисную основу известную кривую и путём сопряжения с ней определенной геометрической фигуры создаём геометрическое построение, состоящее из двух геометрических фигур. Описывая движение точки, общей для двух фигур, выводим новую зависимость, функцию, описывающую новую кривую.

Рассмотрим геометрическое построение на рис. 1.

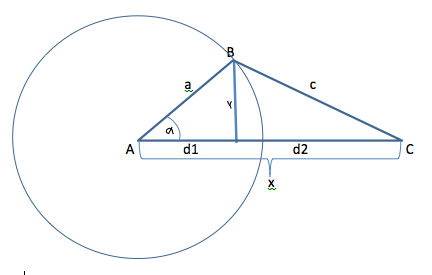
Рис. 1

Высота«γ» может быть выражена равенством: γ = аsinα

Величина «х» может быть выражена как сумма оснований встроенных треугольников, имеющих общую сторону «γ»

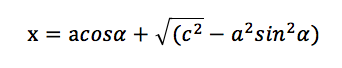
В итоге получаем систему из двух линейных уравнений с двумя неизвестными. Эта система является параметрическим уравнением овала.

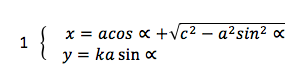
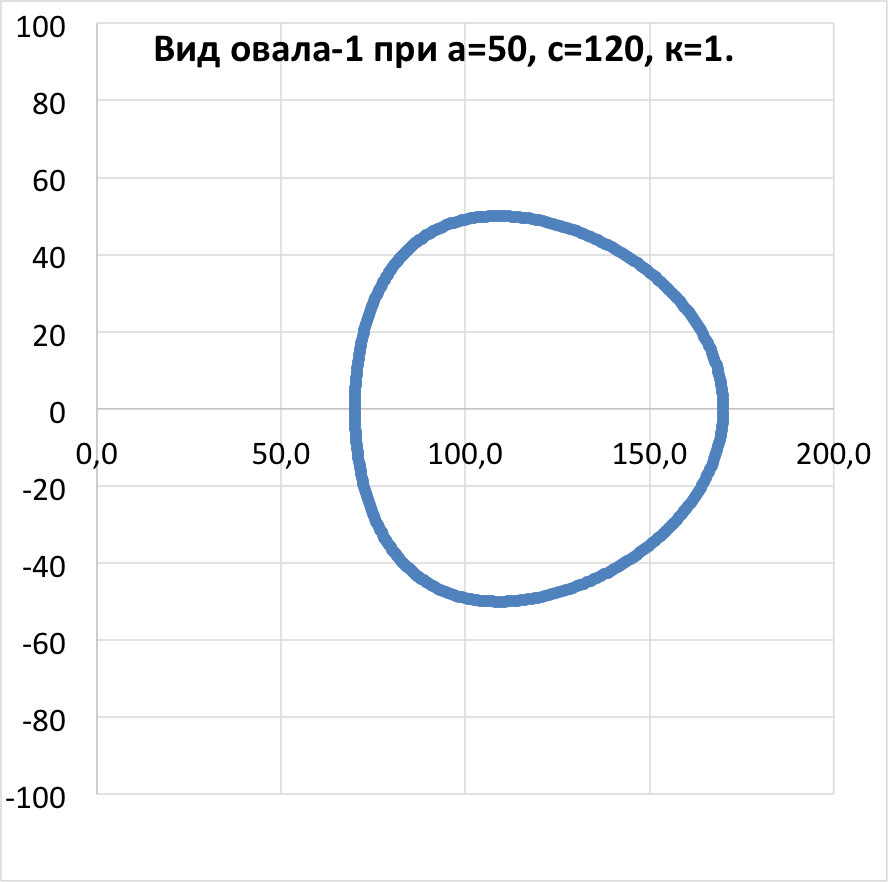
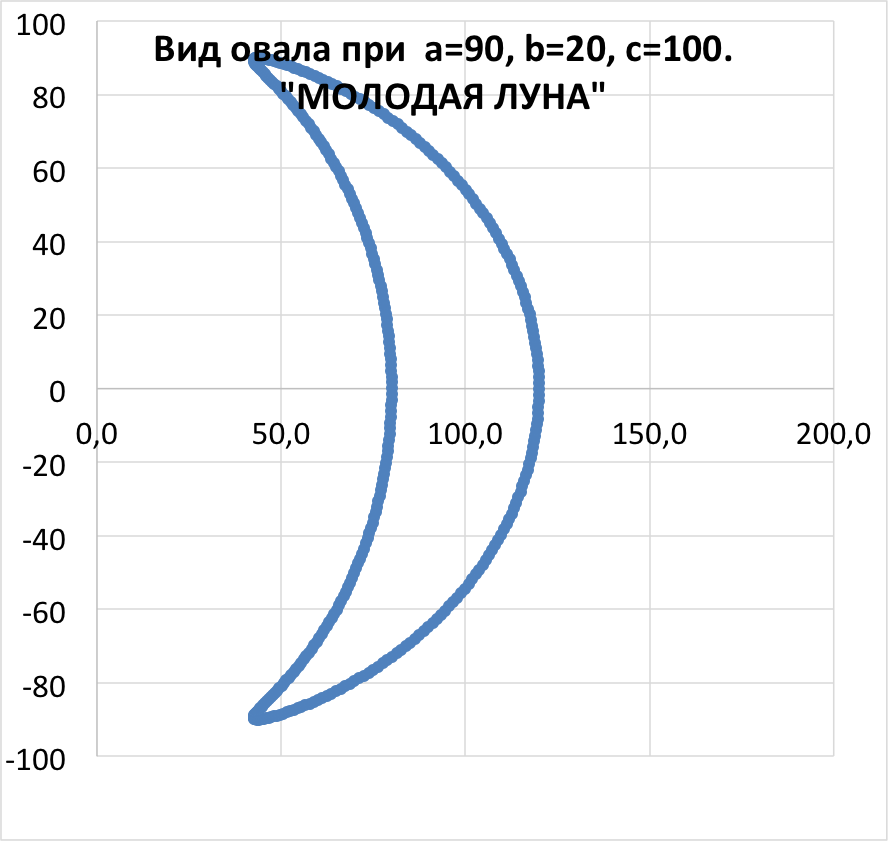
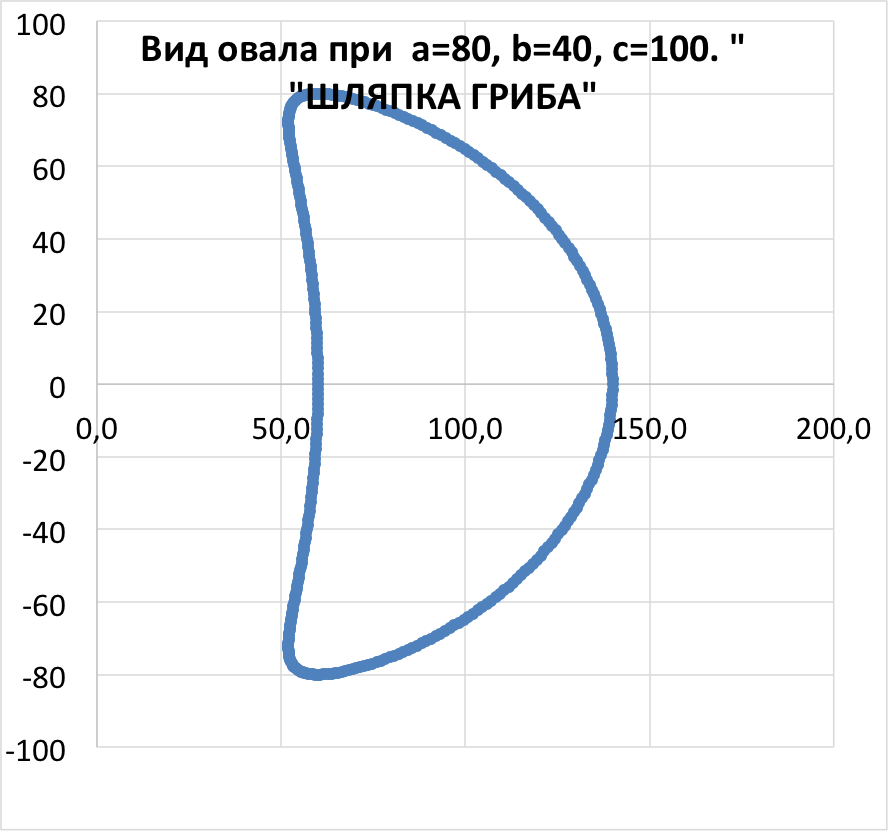
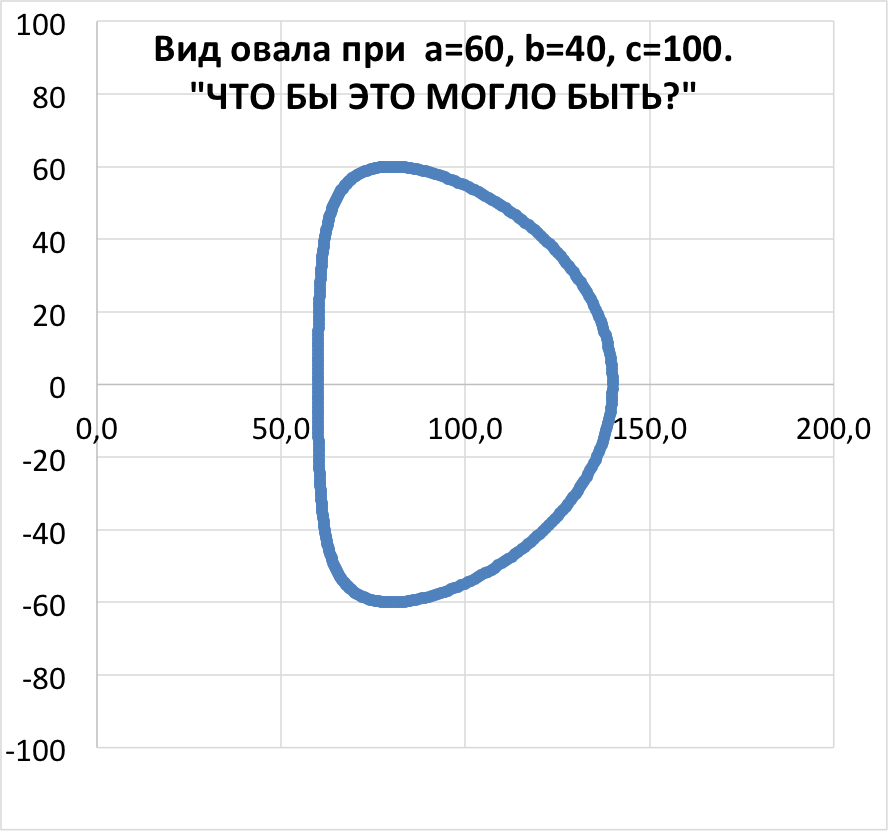
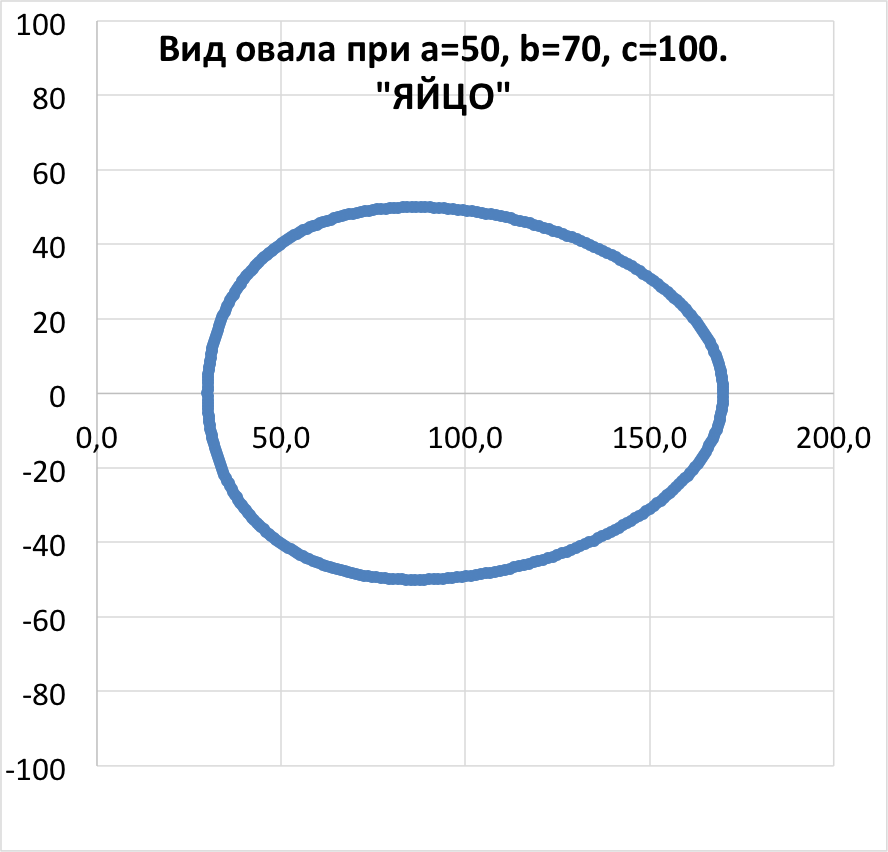
Овалы, описываемые этим уравнением, являются выпуклыми, стабильными и яйцевидными. Последовательно задаваясь различными значениями постоянных а,c и k, получим семейство овалов. Коэффициент «k» введён в формулу произвольно в утилитарных целях (придание овалу желаемой растянутости по горизонтальной оси) и при исследованиях свойств кривых должен быть отброшен.

Математика бесстрастно отражает реальность. В частности уравнение 1 является математическим выражением кинематики двигателя внутреннего сгорания. Сопоставим: постоянная «а»- расстояние от оси коленчатого вала до оси плеча вала, на котором сидит шатун; постоянная «с» – шатун; вершины А, В и С – оси кинематической системы вал-шатун-поршень. Значение величины «x» – путь проходимый поршнем в цилиндре двигателя.

Рассмотрим геометрическое построение на рис. 2.

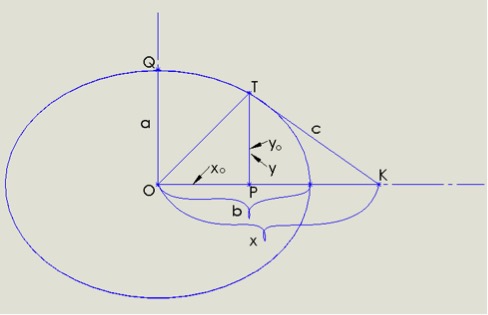
Рис. 2

Имеем треугольник ОТК, вершина Т которого лежит на линии эллипса, основание треугольника ОК лежит на оси абсцисс, вершина О находится в начальной точке системы координат, общей для обеих фигур. C вершины Т треугольника ОТК опустим высоту ТР, обозначив её символом «у». Сторону ТК треугольника ОТК обозначим буквой «с». Стороны ОТ и ОК образуют угол альфа. Величины х° и у° являются координатами геометрических точек, описывающих эллипс с большой полуосью “b” и малой полуосью “a”.

Основание ОК треугольника ОТК будет являться искомой величиной «х». Высота ТР будет искомой величиной «у». Угол «α» – параметр (переменная). Последовательно задаваясь значениями угла «α», передвигаем точку Т по линии эллипса.

Далее по алгоритму, описывая движение точки, общей для обеих фигур, получаем систему из двух уравнений:

При рассмотрении характеристик уравнения 2, оказывается, что при условии равенства полуосей эллипса ( а=b ), эллипс перерождается в окружность и уравнение 2 превращается в уравнение 1, откуда следует, что уравнение 1 является частным случаем уравнения 2. По этой причине в рамках данной статьи параметрическое уравнение 2 назовём универсальным уравнением овалов.

При анализе способов нахождения новых функциональных зависимостей просматривается общая закономерность. В обоих случаях берётся за базисную известная замкнутая кривая (окружность, эллипс), к ней пристраивается треугольник, имеющий общие с базисной фигурой элементы – угол, точку, сторону. Далее проводятся поиски математического выражения изменяющихся параметров треугольника, как функций угла, общего для обеих фигур. Это уже метод.

Резюмируя вышеизложенные соображения, можно констатировать то, что универсальное уравнение овалов

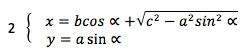
Будущее универсального уравнения овалов — во всестороннем исследовании его свойств. Призываю к исследованиям нового семейства овалов всех неравнодушных к этой теме.