Введение
Мы уже рассказывали об одном проекте для Bauman Racing Team, когда pSeven помог команде откалибровать модель динамики шин болида. Подробнее об этом: «Гоночная команда Bauman Racing Team использовала pSeven для идентификации модели динамики шин».
Сегодня представляем еще один пример внедрения. В данном проекте группа студентов команды Bauman Racing Team оптимизировала точки крепления задней подвески своего нового гоночного болида BRT-8D с помощью pSeven.
От точек крепления подвески напрямую зависит ее кинематика. А от последней, в свою очередь, зависит скорость прохождения поворотов автомобилем. Удачная с точки зрения кинематики конструкция подвески была ранее получена на болиде BRT-7. Такой результат, в первую очередь, был достигнут благодаря компоновочным решениям, что позволило реализовать длинные рычаги подвески. Увеличение длины рычага уменьшает диапазон изменения установочных параметров колеса.
Из-за конструктивных особенностей задняя часть рамы нового болида BRT-8D получилась слишком широкой, поэтому рычаги задней подвески стали существенно короче, что отрицательно повлияло на кинематику (рис. 1).

Рис. 1. Задняя подвеска BRT-8D
Команда Bauman Racing Team разработала математическую модель подвески BRT-8D в программном комплексе Amesim (рис. 2).
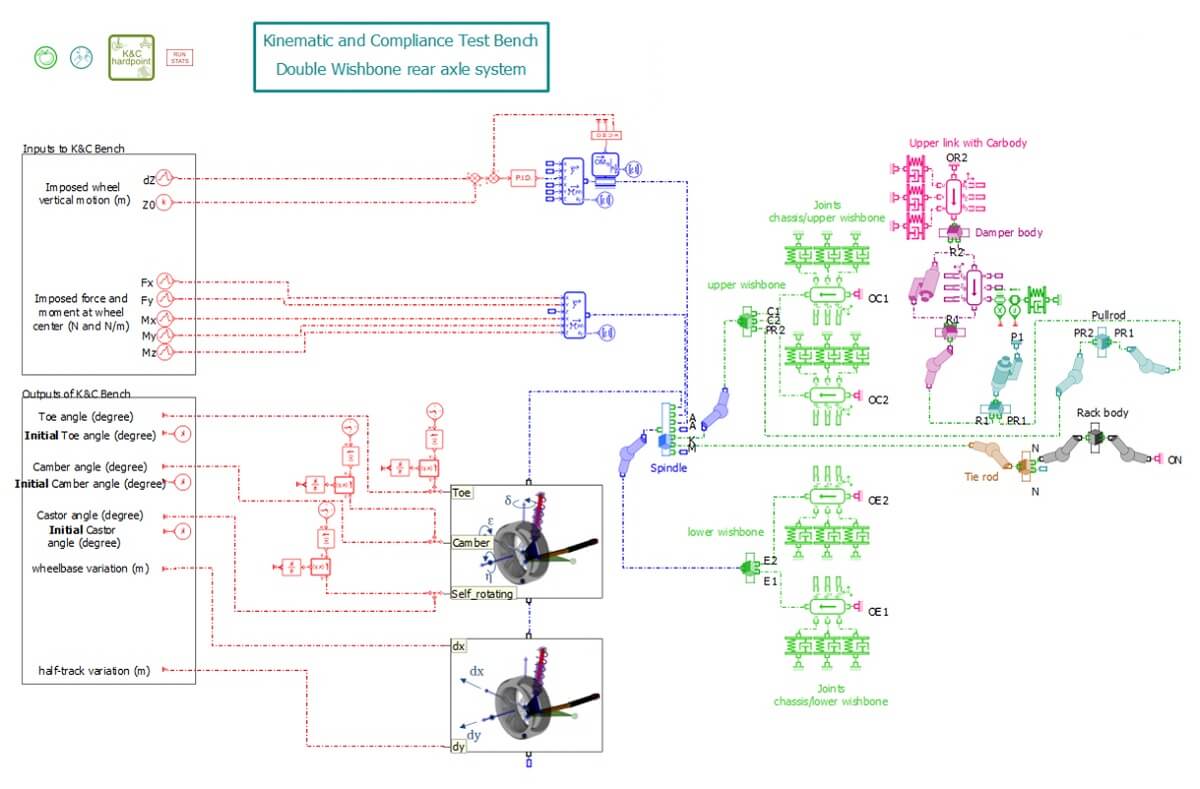
Рис. 2. Математическая модель подвески в Amesim
Теперь, моделируя движение колеса, можно получить графики изменения его установочных параметров (рис. 3).
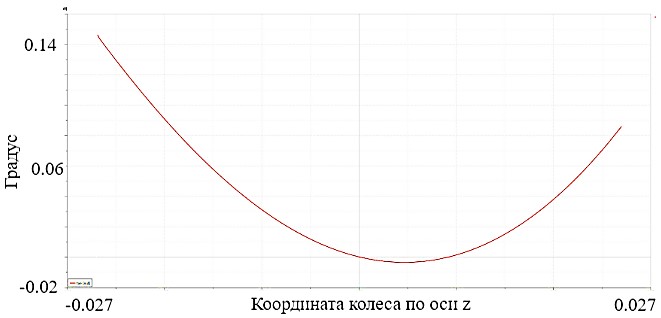
a)
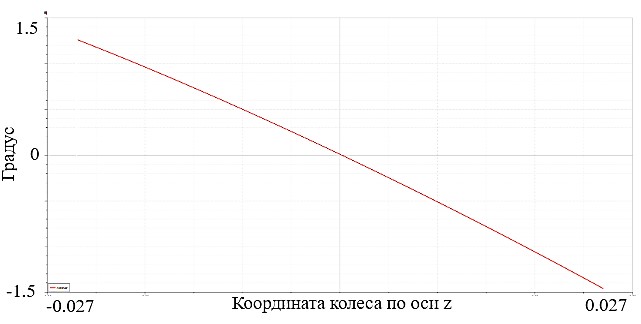
б)
Рис. 3. a) График схождения BRT-8D; б) График развала BRT-8D
Зависимости углов установки колеса от его перемещения совпали с таковыми в программе Lotus Kinematic Suspension, что говорит о том, что разработанная математическая модель верна.
Постановка задачи
В задаче требовалось определить такие точки крепления задней подвески, которые позволили бы максимально приблизить кинематику BRT-8D к кинематике BRT-7. Рассматривались следующие входные параметры:
- координаты точки переднего крепления верхнего рычага к несущей конструкции;
- координаты точки заднего крепления верхнего рычага к несущей конструкции;
- координаты точки переднего крепления нижнего рычага к несущей конструкции;
- координаты точки заднего крепления нижнего рычага к несущей конструкции;
- координаты точки крепления реактивной тяги к колесно-ступичному узлу;
- координата точки крепления реактивной тяги к несущей конструкции.
Существуют два метода оптимизации подвески:
- создание подвески с необходимыми параметрами с нуля;
- улучшение уже имеющихся точек крепления подвески.
Первый метод невероятно сложен в реализации, а также требует большого количества вычислительных ресурсов. Поэтому команда решила выбрать второй подход и использовать эффективные алгоритмы оптимизации в pSeven.
Таким образом, были сформулированы цели оптимизации:
- минимизировать разницу между графиками схождения BRT-8D и BRT-7;
- минимизировать разницу между графиками развала BRT-8D и BRT-7.
Трудности
- сложная зависимость кинематики подвески от точек ее крепления, которая носит нелинейный и неочевидный характер;
- бесчисленное множество возможных вариантов крепления подвески к несущей конструкции, рассмотреть каждый из которых нет возможности.
Решение
Первая попытка решить задачу оптимизации была безусловной. Графики развала и схождения получились очень похожими на желаемые, но точки крепления невозможно было реализовать на автомобиле. Кроме того, все остальные параметры говорили о том, что эта подвеска не соответствует заданным требованиям.
Для получения желаемой кинематики подвески с возможностью компоновки на несущей конструкции недостаточно просто получить требуемые графики установки колес. Необходимо, чтобы параметры удовлетворяли определенным ограничениям.
Первое ограничение: крепление трех точек подвески (2, 4, 6) к плите, которая является частью несущей конструкции (рис. 4).
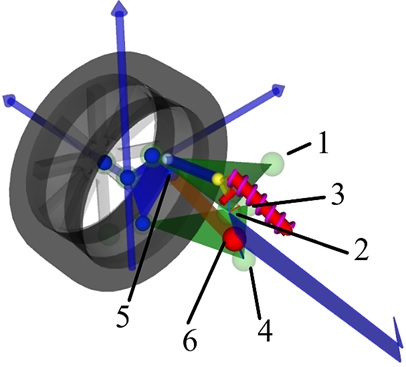
Рис. 4. Задняя подвеска BRT-8D в Amesim: синим цветом выделена плита
Зная расположение плиты в пространстве, получаем её математическое уравнение вида Ax+By+Cz+D=0. В Amesim был реализован «cупер компонент», который подставляет координаты точек 2, 4, 6 в данное уравнение. Для каждого такого равенства было создано ограничение в pSeven (рис. 5):
- Upperlimit — задняя точка крепления верхнего рычага;
- Lowerlimit — задняя точка крепления нижнего рычага;
- Rodlimit — точка крепления реактивной тяги.
Чтобы сумма Ax+By+Cz+D равнялась нулю, точка должна соответствовать строгому условию принадлежности плоскости, выполнить которое практически невозможно, поэтому была введена погрешность ±10^(-4) м.
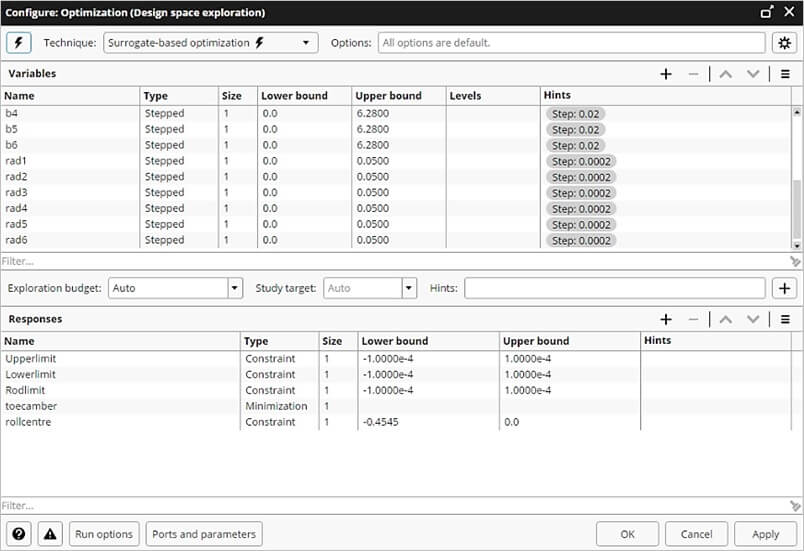
Рис. 5. Настройка оптимизатора
Вторым ограничением является координата центра крена, которая напрямую зависит от расположения рычагов. Центр крена задней оси должен находиться выше центра крена передней оси, но при этом ниже центра тяжести автомобиля. Координата высоты центра крена передней оси в системе отсчета -0.4545 м, а центра тяжести автомобиля 0 м. Поэтому именно такой диапазон значений установлен для переменной “rollcentre” (рис. 5).
Так как для оптимизации получилось слишком много изменяемых параметров, а для соблюдения условий потребовалось установить маленький шаг их изменения, с целью уменьшения времени расчета разности графиков развала и схождения были сведены к одной переменной “toecamber”.
Для решения задачи оптимизации модель Amesim была интегрирована в расчетную схему pSeven и подключена к блоку Design space exploration, в котором в качестве алгоритма была выбрана оптимизация на основе суррогатных моделей (рис. 6).
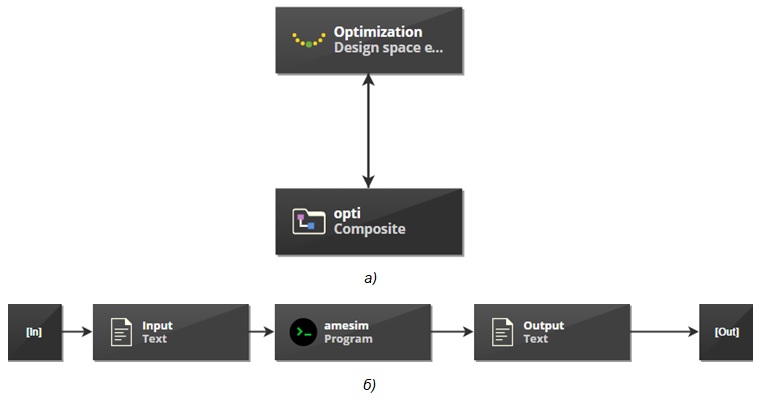
Рис. 6. a) Оптимизация в pSeven; б) содержимое композитного блока — интеграция с расчётной моделью в Amesim
Результат
В результате оптимизации была получена кинематика, превосходящая исходную модель по диапазону изменения углов установки колёс с соблюдением всех необходимых условий (рис. 7–8).
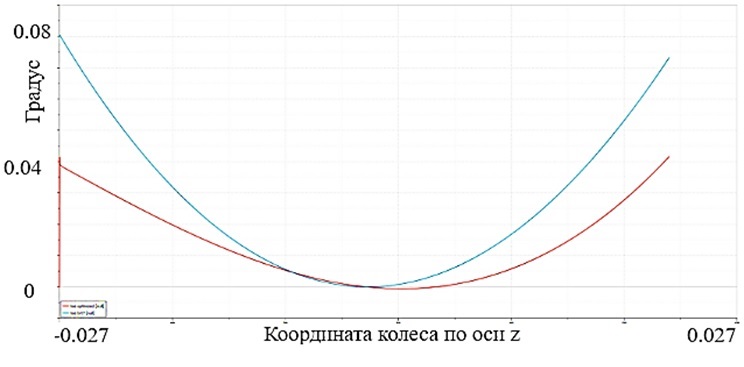
Рис. 7. График схождения: синий цвет — желаемая кривая, красный цвет — полученный результат
Площадь под графиком схождения составляла 2.1172 условных единиц, а после оптимизации стала равной 0.731234. Площадь под графиком уменьшилась более чем на 65%.
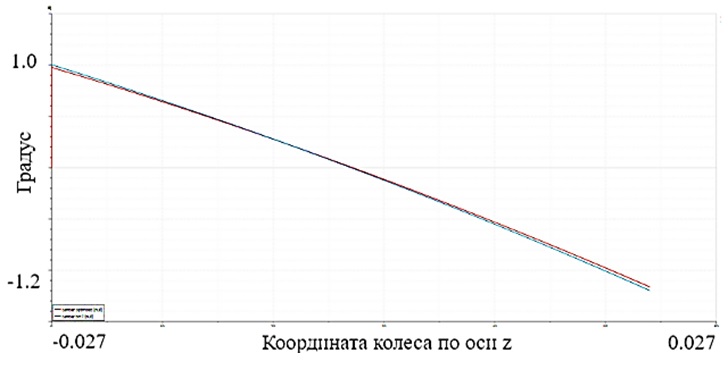
Рис. 8. График развала: синий цвет — желаемая кривая, красный цвет — полученный результат
Площадь под графиком развала составляла 1.38555 условных единиц, а после оптимизации составила 1.45181. Площадь под графиком уменьшилась почти на 5%.
Однокритериальная оптимизация заняла меньше 10 мин, а её бюджет составил 472 обращения к расчетной модели.
Компания DATADVANCE — независимый разработчик программного обеспечения, предоставляющий промышленные программные решения и консалтинговые услуги в области автоматизации инженерных расчетов, оптимизации и предиктивного моделирования. Офисы компании находятся в Москве и Тулузе (Франция).
www.datadvance.ru
