Длина дуги — поиски универсальной формулы

Предисловие Берды Овезова

В июне 2017 года на портале isicad.ru была опубликована моя статья «Яйцевидный овал как производная». Я надеюсь, что читателей заинтересует новая публикация — теперь уже с соавтором.

На этот раз всё началось с того, что при решении прикладной задачи по раскройке винтообразной лопасти ветрового генератора мы столкнулись с необходимостью определить радиус кривизны кромки лопасти. В поисках ответа мы привычно обратились к справочнику М.Я. Выгодского, 1987 г., издание двадцать седьмое, исправленное, и нашли там «Формулу длины дуги Гюйгенса». Кромка нашей лопасти представляла собой дугу, описанную в справочнике, но в формуле Гюйгенса мы ответа на свой вопрос не нашли. Поиски этого радиуса, приведшие к новому пониманию природы дуги Гюйгенса, описаны в нашей статье.

В справочнике по элементарной математике М. Я. Выгодского, в разделе «Геометрия», §15а, представлена формула голландского ученого Х. Гюйгенса (1629-1695) [1], выражающая длину дуги. Представим выписку из §15а «Формула длины дуги Х. Гюйгенса».

Задача формулируется следующим образом [2]:

«На практике часто требуется найти длину дуги, данной на чертеже или в натуре, причем неизвестно, какую часть окружности составляет дуга и каков её радиус».

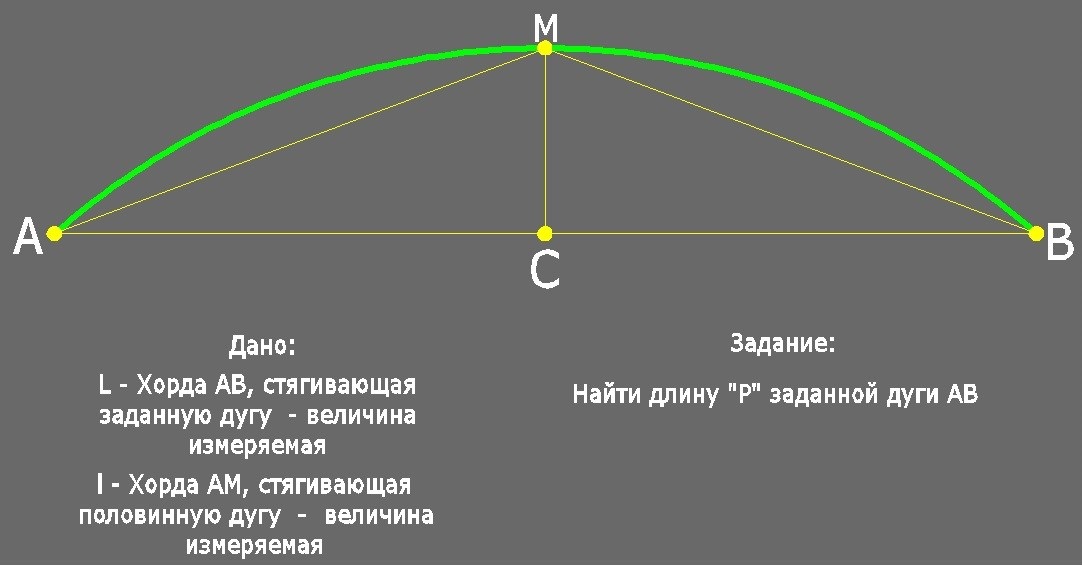
Рис. 1

«Отметим на данной дуге АВ (рис. 1) её середину М (она лежит на перпендикуляре СМ, проведенном к хорде АВ через её середину С). Затем измерим хорду АВ и хорду АМ, стягивающую половинную дугу. Длина дуги АВ выражается (приближенно) следующей формулой Гюйгенса*):

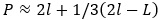,      (1)

где ℓ = АМ, L = AB

Относительная погрешность этой формулы составляет около 0,5%, когда дуга АВ содержит 60°».

В 17-м веке современников Х. Гюйгенса заявленная степень точности, видимо, вполне удовлетворяла. Да и в следующие века, вероятно, эта формула исправно служила, так как никто за это время не усомнился в незаменимости этого математического выражения. Авторам для решения прикладной задачи было необходимо найти радиус кривизны кромки винтообразной лопасти. В поисках ответа мы обратились к «Формуле длины дуги Гюйгенса», но оказалось, что Гюйгенс в своей формуле прекрасно обошелся без радиуса окружности. В дальнейшем для простоты изложения эта окружность будет упоминаться как образующая. Обозначилась задача: найти математическое выражение длины дуги, которое содержало бы в себе радиус неизвестной пока образующей окружности. Выяснилось, что уравнение, выражающее длину дуги, давно существует [3]:

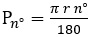,      (2)

где 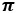= 3,14159… — универсальная константа, r — радиус окружности, содержащей дугу, n° — внутренний угол сектора, образованного дугой. Но уравнение (2) в геометрии выражает длину дуги при известной образующей окружности с заданным радиусом r и заданным центральным углом n°. Следовательно, предстоит решить задачу по наполнению уравнения новым содержанием, преображающим его в математическое выражение, описывающее дугу неизвестной окружности.

Начнем с того, что в самой формулировке задачи [2] предполагается, что исследуемая дуга является частью неизвестной окружности. Если копать в этом направлении, задача сводится к нахождению образующей окружности с применением вспомогательных геометрических построений и нетривиальных геометрических функций.

Немного из истории тригонометрии, цитата из справочника:

«Известный немецкий астроном XV века Региомонтан (1436 - 1476) составил обширные таблицы синусов за два столетия до времен творчества Гюйгенса. За таблицами Региомонтана последовал ряд других, ещё более подробных. Друг Коперника Ретикус (1514-1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в 1596 году его учеником Ото». [4]

Гюйгенс, как большой ученый, не мог быть неосведомленным об аспектах применения тригонометрических функций в решении широкого круга геометрических задач. Возникает вопрос: почему Гюйгенс не пошел по этому пути? Возможно, формула, предложенная Гюйгенсом человечеству, сама по себе не была целью его исследований. Можно лишь предположить, что Гюйгенс вывел формулу длины дуги как инструментарий для решения какой-то промежуточной прикладной задачи, которая приближала его к цели в его основных исследованиях. Ну а после Гюйгенса, видимо, никому и в голову не приходило попытаться улучшить инструмент, ведь относительная погрешность мала: всего одна двухсотая — ноль целых, пять тысячных. Но не в наши времена. По этому поводу можно лишь пошутить, что в наше время допустимая погрешность — это размерности, приближающиеся к «планковской длине» [5].

На практике подавляюще большое множество кривых несёт в себе фрагменты, являющиеся дугой Гюйгенса. К примеру, в начертательной геометрии и, как следствие, в аналитической геометрии, это наблюдается на каждом шагу — это проекции двумерных и трехмерных кривых на плоскость. В интернете встречается множество решений различных задач подобного рода при помощи коротеньких дифференциальных уравнений, пристегнутых к онлайн калькулятору, то есть к алгоритму, зашитому в компьютерную программу. Щелчок по клавише — и задача действительно решается. О крайностях в этом направлении хорошо сказал Владимир Талапов: «Возможны и другие сходные по глубине понимания варианты, недалеко ушедшие от своего недавнего предшественника, — “Сделайте нам проект в электронном виде!”» [9].

Но наша песня не об этом. Дело в том, что в Евклидовой геометрии, где царит железобетонная иерархия причинно-следственных связей, формула (даже не уравнение) Гюйгенса, при всём к нему уважении, выглядит экзотическим, чужеродным телом. Со всей очевидностью приходится признать, что вопрос длины дуги, обозначенный Гюйгенсом, вплоть до наших дней остаётся открытым. Подчеркнём, в рамках Евклидовой геометрии.

Однако приступим. На рис. 2, с середины малых хорд АМ и МВ строим перпендикуляры вплоть до точки их взаимного пересечения. Применение перпендикуляров является ключевым моментом решения нашей задачи. Точка пересечения перпендикуляров является центром искомой образующей окружности. Основная часть задачи решена, найден центр образующей окружности. Теперь любой отрезок, проведённый от центра до линии дуги, будет радиусом образующей окружности. Отрезок МО на рис. 2 является радиусом образующей окружности и гипотенузой треугольника ОКМ.

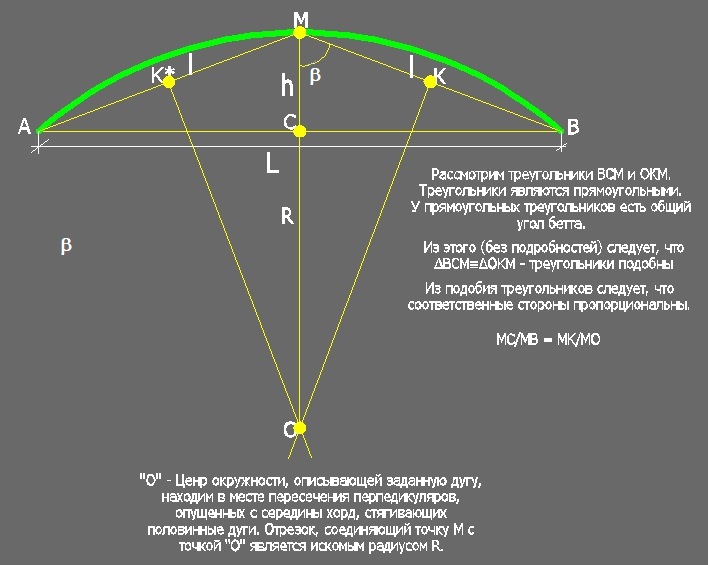
Рис. 2

В своей формуле Гюйгенс использует две измеряемые величины: хорду АВ и хорду АМ(МВ), стягивающую половинную дугу. Воспользуемся ими и мы.

Рассмотрим на рис. 2 треугольники ΔМВС и ΔМКО. Эти два прямоугольных треугольника имеют общий угол β. Опуская подробности, констатируем, что эти треугольники подобны. Тогда должно выполняться правило пропорциональности:

.

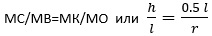Получаем выражение радиуса искомой окружности:

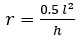,                             (3)

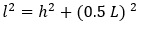где .          (4)

Вставим выражение (3) в уравнение (2) и получим уравнение длины дуги:

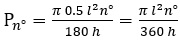.      (5)

Если мы решим избавиться от величины малой хорды l, вставим выражение (4) в уравнение (5), и уравнение длины дуги примет следующий вид:

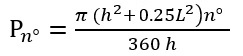.        (6)

Задача в принципе решена. Найден центр образующей окружности, найдено выражение радиуса образующей окружности, составлено уравнение длины дуги. Осталось найти математическое выражение угла n и вставить его в уравнение (6).

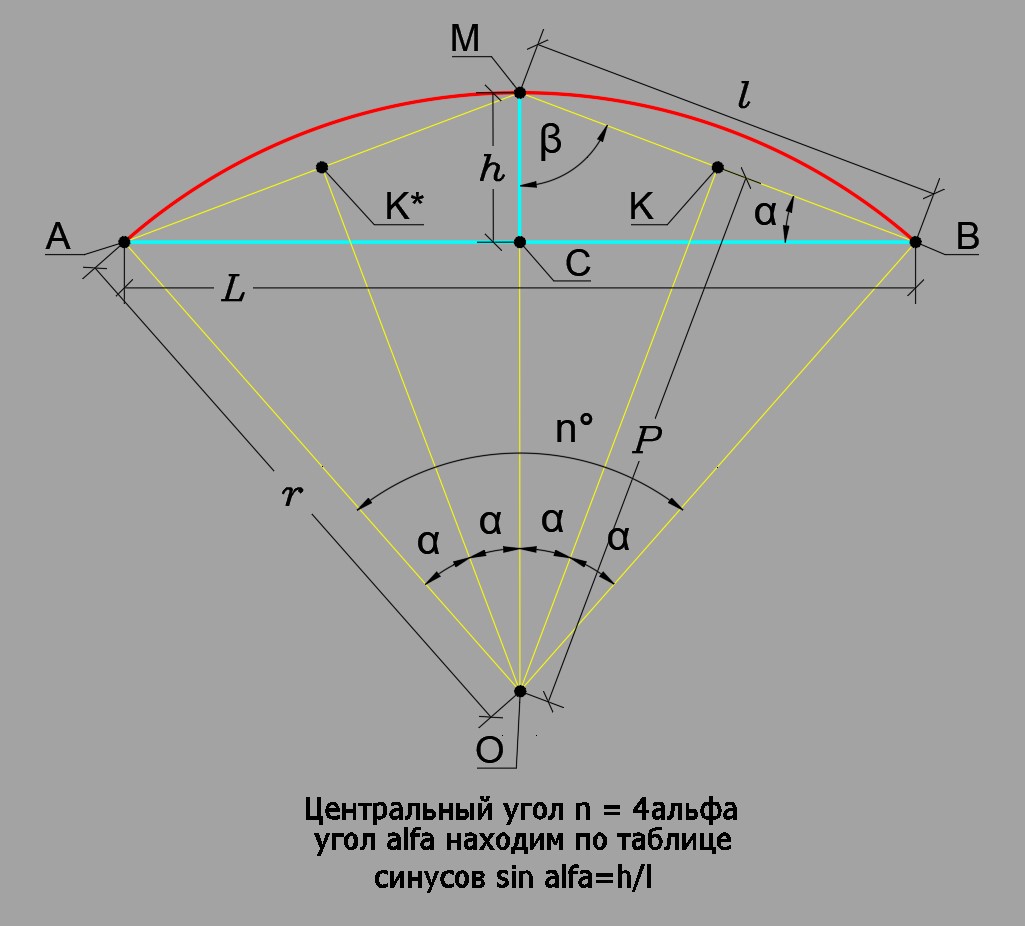
Рис. 3

На рис. 3 видно, что центральный угол n, образованный исследуемой дугой и двумя стягивающими радиусами, равен сумме четырех углов альфа: n = 4α.

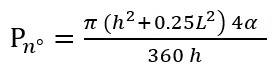.         (7)

Угол, определяющий функцию, может быть выражен в двух качествах — радианах или градусах. Более того, функция, как в нашем случае, может содержать и радианы, и градусы. Существует способ перевода радианов в градусы — это умножение тригонометрической функции на 180/π.

Умножим уравнение (7) на 180°/π и получим

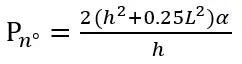.         (8)

Угол альфа, в свою очередь, характеризуется выражением

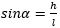или .

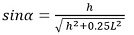Это выражение нам вскоре понадобится.

В принципе, можно на этом остановиться, сославшись на формулу синуса альфа и указав на то, что угол α вычисляется по таблице синусов и его значение вставляется в уравнение. А можно воспользоваться обратными тригонометрическими (круговыми) функциями. Но вначале коротко об обратных функциях, приведем цитату из справочника:

«Соотношение х = sin y позволяет с помощью таблиц найти как «х» по «у», так и «у» по данной величине «х» (не превышающей единицу по абсолютной величине). Таким образом, можно считать не только синус функцией угла, но и угол функцией синуса. Этот факт находит внешнее выражение в записи у = arcsin x. Например вместо 1/2 = sin 30° можно написать 30° = arcsin 1/2. Нахождение же синуса по углу и угла по синусу совершается по одним и тем же таблицам, в которых к тому же выделено название «синус», а «арксинус» не упоминается. Поэтому никакого особого действия, результатом которого был бы арксинус, усматривать не приходится; и вообще в пределах элементарной математики введение этого понятия, по существу, не оправдывается. В высшей же математике арксинус появляется как необходимый результат некоторого действия (интегрирования), и именно здесь возникло понятие арксинуса и его обозначение». [6]

Резюмируя изложенное, даем определение: arcsin х есть угол, синус которого равен x. На языке математики это записывается как sin arcsin х = x. Это выражение относится к основным соотношениям обратной функции [7].

Тогда

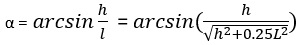.         (9)

Итак, после того как арксинус выявил себя в элементарной математике как проекция функции, несущей смысл только в высшей математике, мы всё же можем воспользоваться им как символом, придающим уравнению законченный вид. Впрочем, при вшивании уравнения в компьютерную программу наличие в уравнении арксинуса требует загрузки в программу всей таблицы синусов, что автоматически преобразует арксинус из символического в конструктивный элемент уравнения.

Вставим выражение (9) в уравнение (8). Уравнение, выражающее длину дуги, примет окончательный вид:

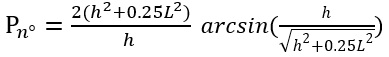,           (10)

где 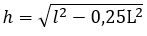следует из выражения (4).     (11)

Во вновь испеченной формуле используются два параметра: хорда АВ и высота h, опущенная с середины исследуемой дуги на середину хорды АВ. Хорда АВ по условиям задания поддаётся измерению. Высота h может быть как измерена, так и легко вычислена (см. выражение (11)).

Исследование завершено, и можно поставить точку, но подведем итоги.

Выведенное уравнение избавляет нас от приближенности формулы Гюйгенса и даёт как искомую длину дуги, так и геометрическое осмысление дуги как носителя свойств образующей окружности. Это как в палеонтологии — по одному найденному зубу определяется вид доисторического животного [8]. Теперь представленная в справочнике задача

«На практике часто требуется найти длину дуги, данной на чертеже или в натуре, причем неизвестно, какую часть окружности составляет дуга и каков её радиус»

выглядит сформулированной не вполне корректно, так как, если и не совсем потеряла смысл, то, несомненно, утратила категоричность истины в последней инстанции. Исследуемая дуга в уравнении (10) приобретает статус кривой, несущей в себе полную информацию об образующей окружности. Уравнение (10) возвращает дугу из состояния приближённости Гюйгенса в поле каузальной определённости Евклидовой геометрии.

Хочется закончить пожеланием: Господа программисты, смело вшивайте в свои программы новорождённое уравнение!

Ссылки

1. Х. Гюйгенс (1629-1685) — голландский механик, физик, математик, астроном, и изобретатель. Один из основоположников теоретической механики и теории вероятности. Википедия.
2. М. Я. Выгодский. Справочник по элементарной математике, 1987г. Издание двадцать седьмое, исправленное. Раздел «Геометрия», §15а, стр. 212.
3. М. Я. Выгодский. Справочник по элементарной математике, 1987 г. Раздел «Геометрия», §15, стр. 211.
4. М. Я. Выгодский. Справочник по элементарной математике, 1987 г. Раздел «Тригонометрия», §3, стр. 247.
5. Планковская длина — это масштаб длины, на которых квантовая гравитация становится актуальной. Планковская длина в 10²⁰ раз меньше диаметра атома водорода. Википедия.
6. М. Я. Выгодский. Справочник по элементарной математике, 1987 г. Раздел «тригонометрия», §24, стр. 273 – 274.
7. М. Я. Выгодский. Справочник по элементарной математике, 1987 г. Раздел «тригонометрия», §25, стр. 275.
8. «Палеонтология как наука была создана ХVIII веке в результате работ Жоржа Кювье (1769-1832) по сравнительной анатомии…» — Википедия.
9. Статья Владимира Талапова “Первое представление книги «BIM для начинающих»” от 23 февраля 2023 года.