
Функциональность для формирования и редактирования модели (продолжение)
Построение сглаживаний рёбер и граней
Традиционно значительное развитие получила функциональность RGK в части построения сглаживаний рёбер и граней. Как известно по прошлым обзорам функциональности ядра, развитие происходит в двух основных направлениях: расширение списка решаемых геометрических задач и совершенствование топологических алгоритмов. В обоих этих направлениях в новой версии разработчиками достигнуты значительные успехи.
Рассмотрим в первую очередь геометрическую часть задачи. Для начала остановимся на обработке ситуации, когда при построении поверхности может получиться самопересечение поверхностей сглаживания. Как известно, ранее в RGK уже были разработаны алгоритмы, которые позволяют бороться с некоторыми типами таких сложностей. В новой версии эти инструменты получили дальнейшее развитие. Во-первых, были улучшены методы поиска границ области самопересечения. Во-вторых, разработана математика коррекции границы такой области — регуляризации задачи — и применена новая математика генерации поверхностей сглаживания для областей сложной формы. Это позволило решать весьма сложные постановки, ранее доступные только паре-тройке геометрических ядер в мире.
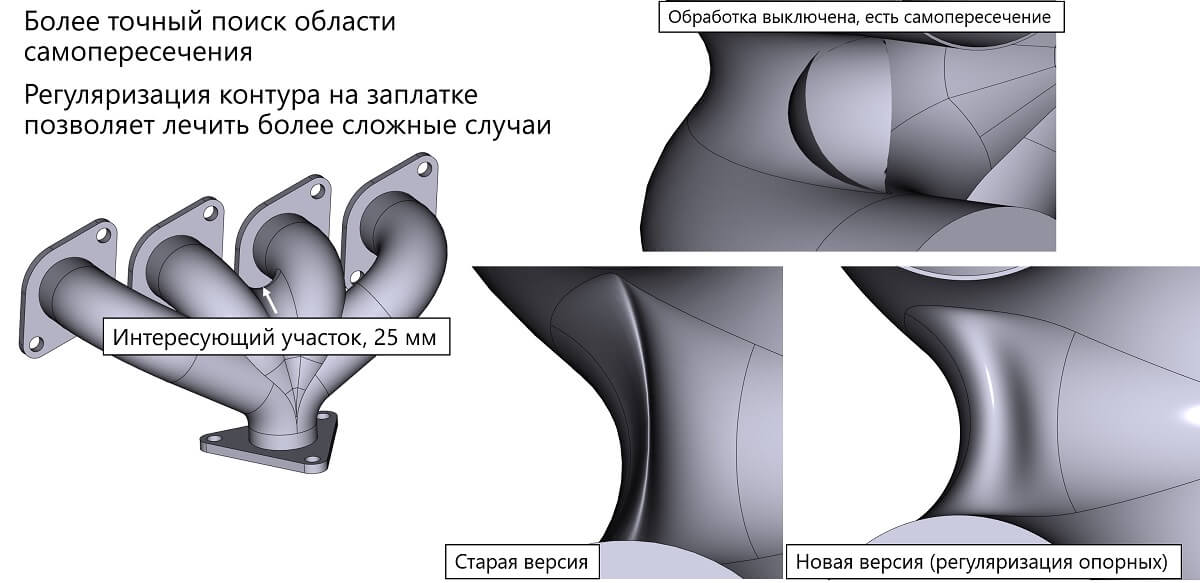
Пример построения сглаживания в зоне самопересечения с применением силу большого радиуса
Добавились новые типы поверхностей сглаживания. В частности, теперь поддерживается переменная ширина поверхности сглаживания.
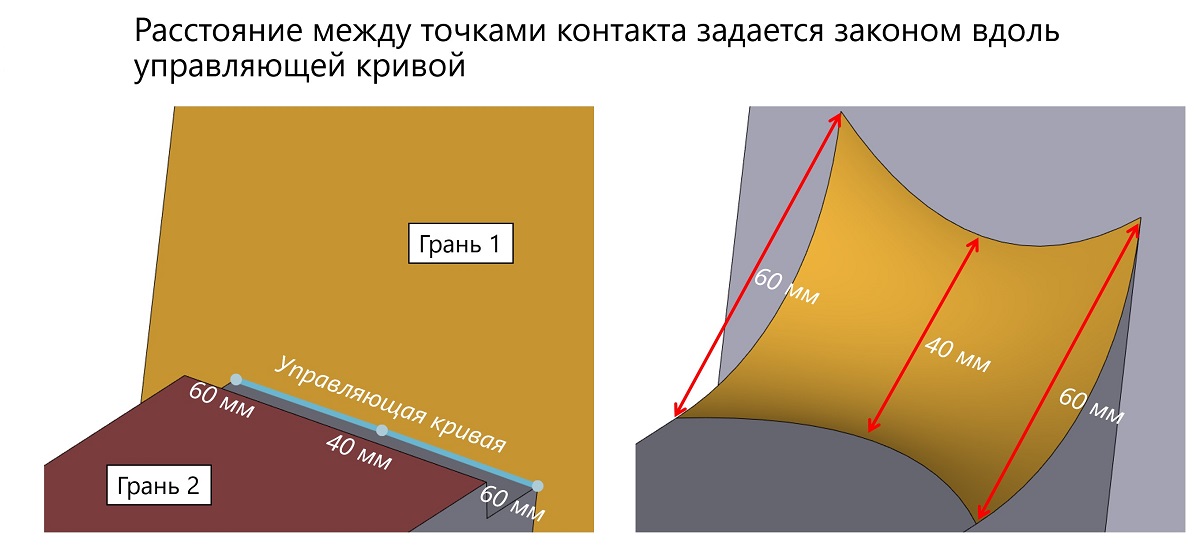
Иллюстрация схемы построения поверхности сглаживания переменной ширины
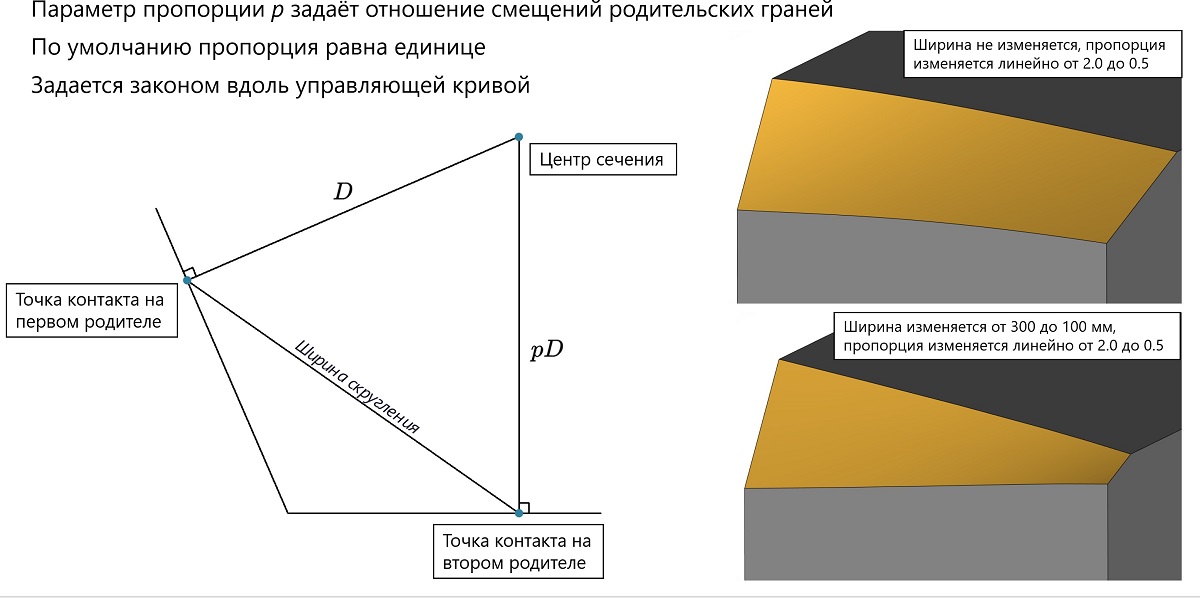
Управляющие параметры режима переменной ширины сглаживания
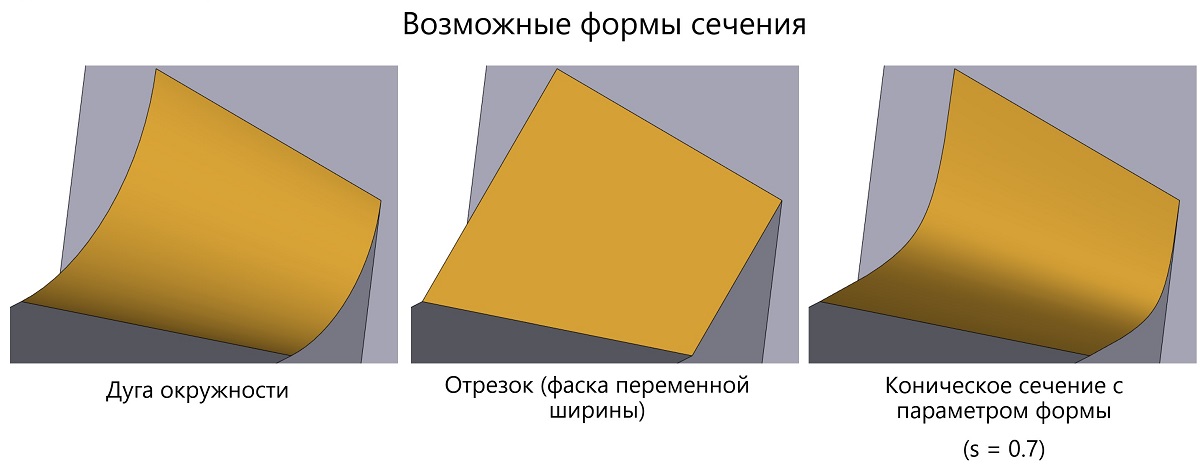
Примеры возможных форм сечений в режиме переменной ширины
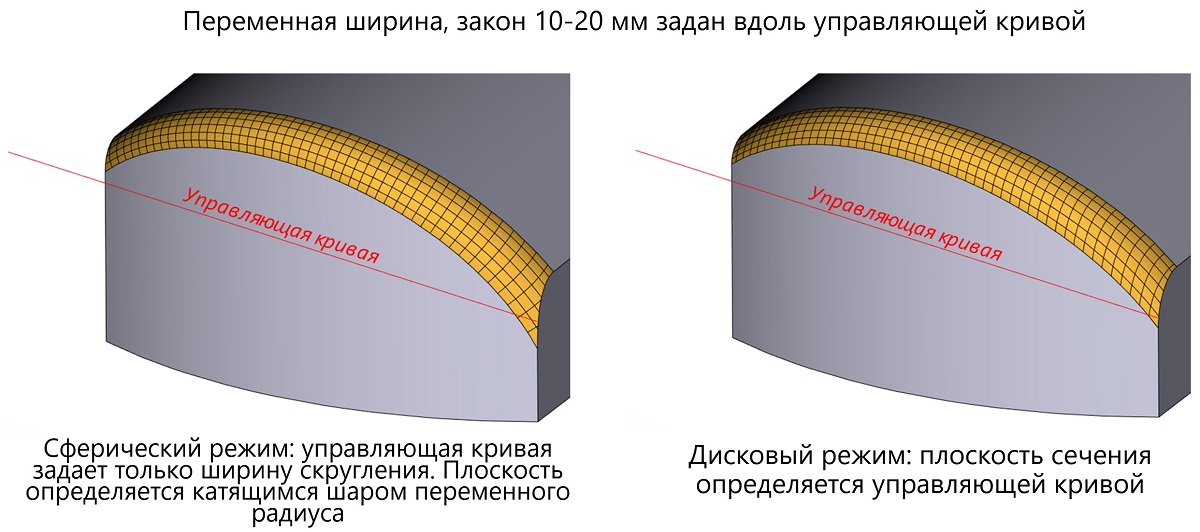
Пример работы нового режима в случае «катящегося шарика» и дискового сглаживания
Завершена работа над так называемым «коническим» сглаживанием, когда величины смещений могут определяться кривыми на сопрягаемых поверхностях. Вот как это выглядит:
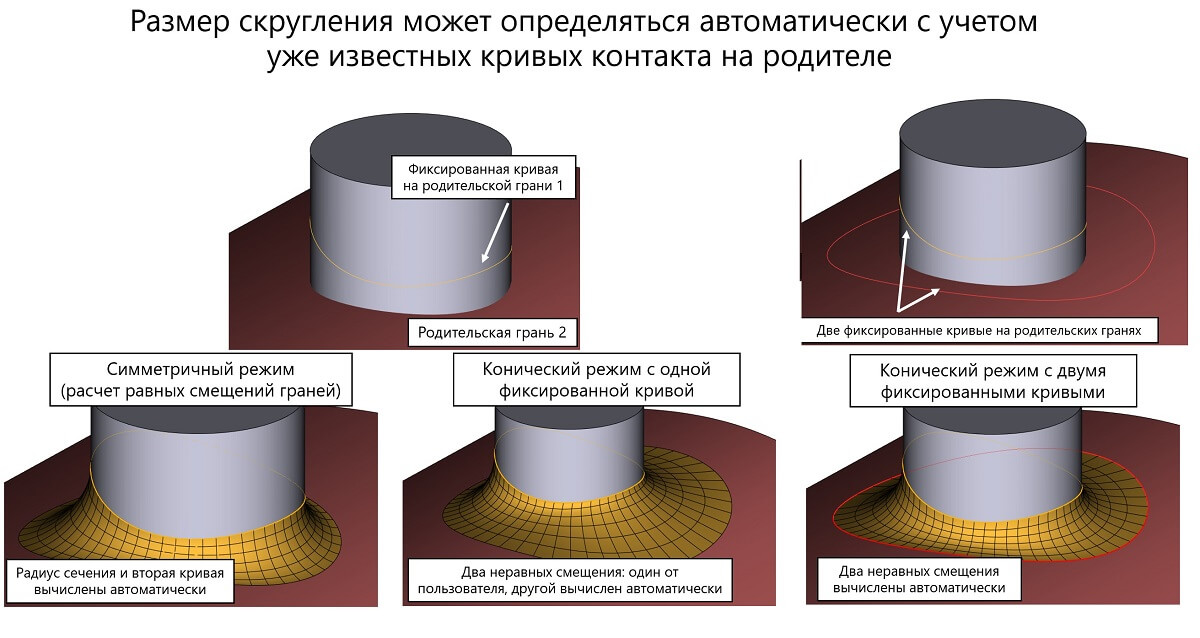
Иллюстрация режимов «конических» сглаживаний
Следует напомнить, что архитектура алгоритмов сглаживания RGK позволяет использовать комбинацию различных параметров операции: формы сечения, ориентации сечения, величин и характеристик смещений и так далее. Более наглядно эти возможности представлены в таблице ниже.
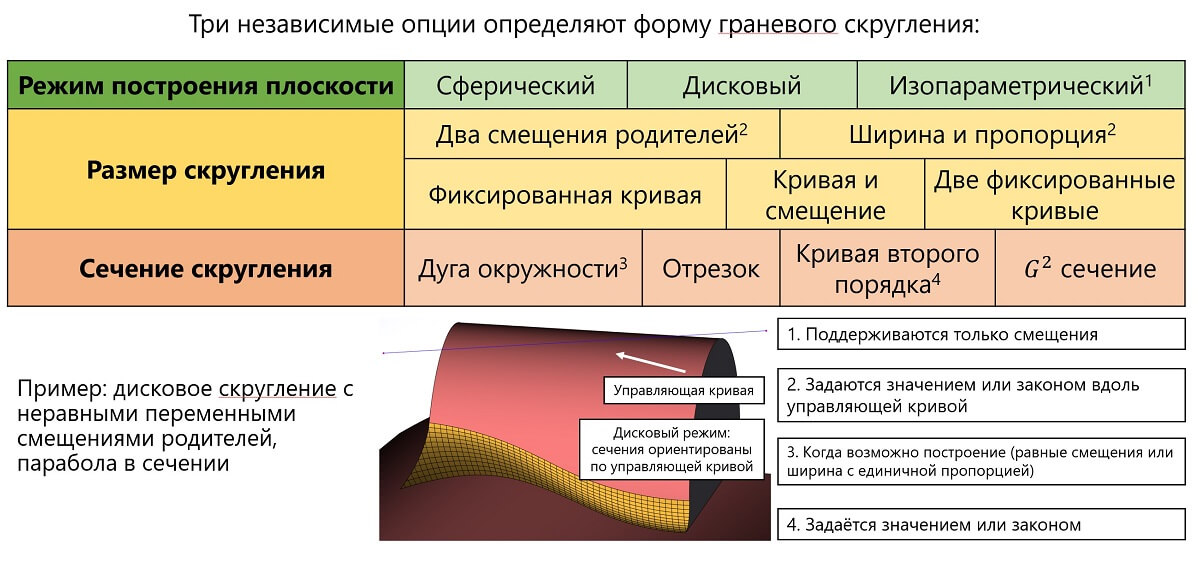
Таблица, иллюстрирующая режимы сглаживания RGK
В настоящее время можно утверждать, что ядро RGK поддерживает все практически значимые комбинации параметров. В этом отношении достигнут паритет с ведущими мировыми геометрическими ядрами. Помимо общих постановок задач, в математике есть большое число важных, но не очень наглядных проблем, которые тем не менее требуют решения для получения практически полезного результата. Осознавая это, разработчики ядра RGK тратят значительные усилия на усовершенствование алгоритмов для обеспечения необходимого качества результата. Работа такого плана ведётся постоянно, хотя результаты не всегда заметны при беглом просмотре. Но качество геометрии, по нашему мнению, крайне важно, и в значительной степени отличает промышленные ядра от других.
Проиллюстрируем эту мысль на одном примере. Рассмотрим сглаживание с переменным радиусом с линейной функцией радиуса. Задача эта уже довольно давно решается в RGK, но качество результата не устраивало разработчиков ядра, так как гладкость поверхности сглаживания на стыках граней не всегда хорошо обеспечивалась именно при честной линейной функции радиуса.
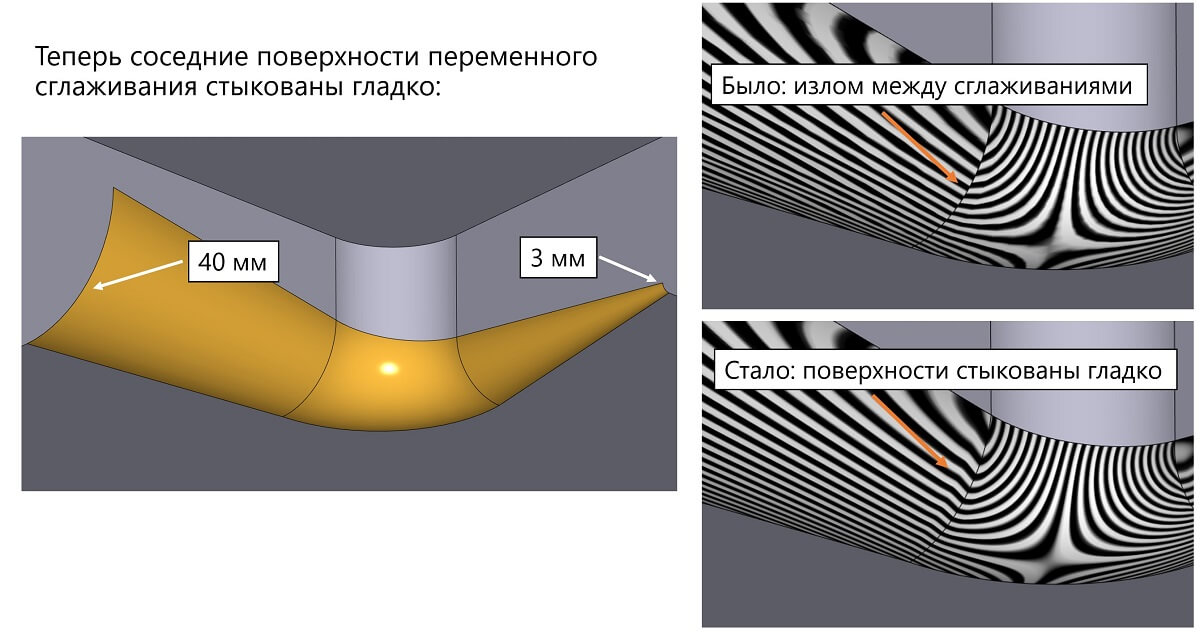
Иллюстрация проблемы излома касательной плоскости при линейном изменении радиуса и поведения алгоритма сглаживания в новой версии ядра
Не будем останавливаться на математических аспектах задачи, отметим только, что подобные решения часто нетривиальны. Прежнее поведение — это не «ошибка алгоритма», как кто-то может подумать, а формально верный ответ в задаче сглаживания. Однако хотелось бы получить поверхность лучшего качества, что было достигнуто в новой версии. Подобного улучшения качества решения задач в различных алгоритмах ядра немало, хотя это, на первый взгляд, и незаметно.
В сглаживании предыдущих версий RGK была заявлена функциональность построения Y-формы при вершинном сглаживании. В новой версии эта функциональность также получила своё развитие. Рассмотрим на примерах, что теперь умеет этот инструмент.
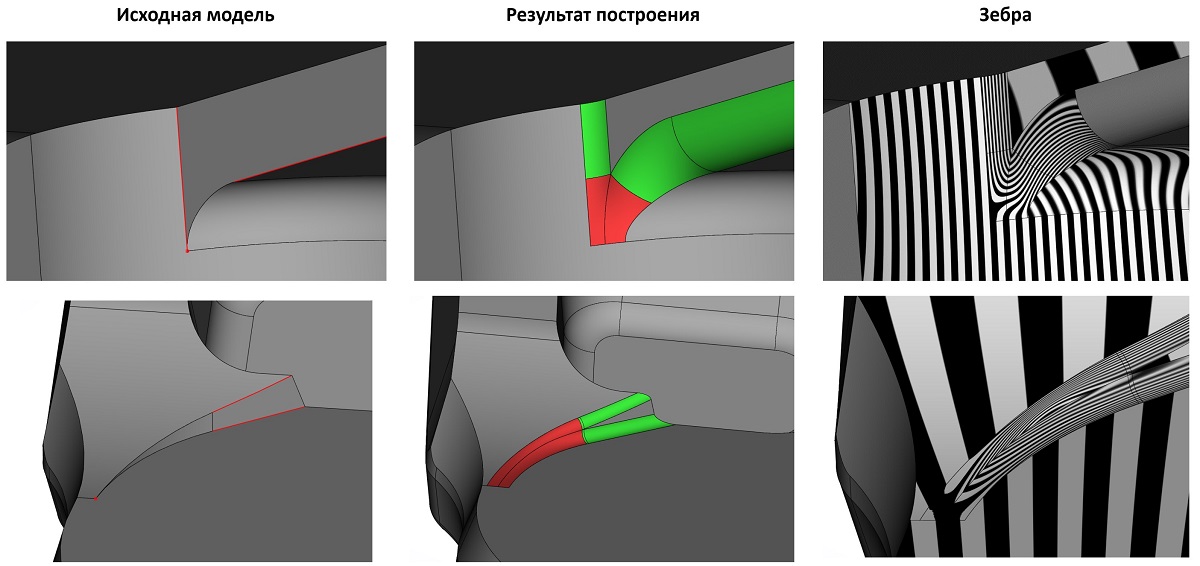
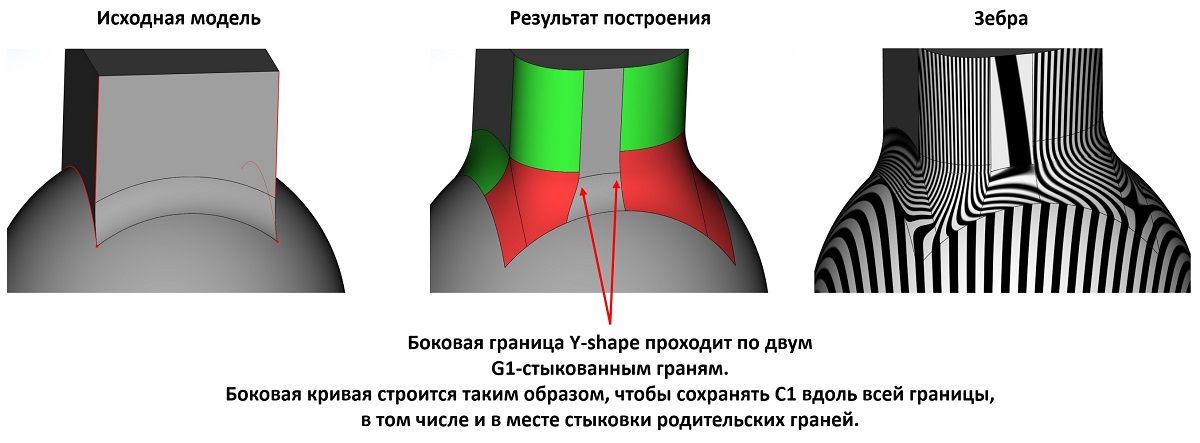
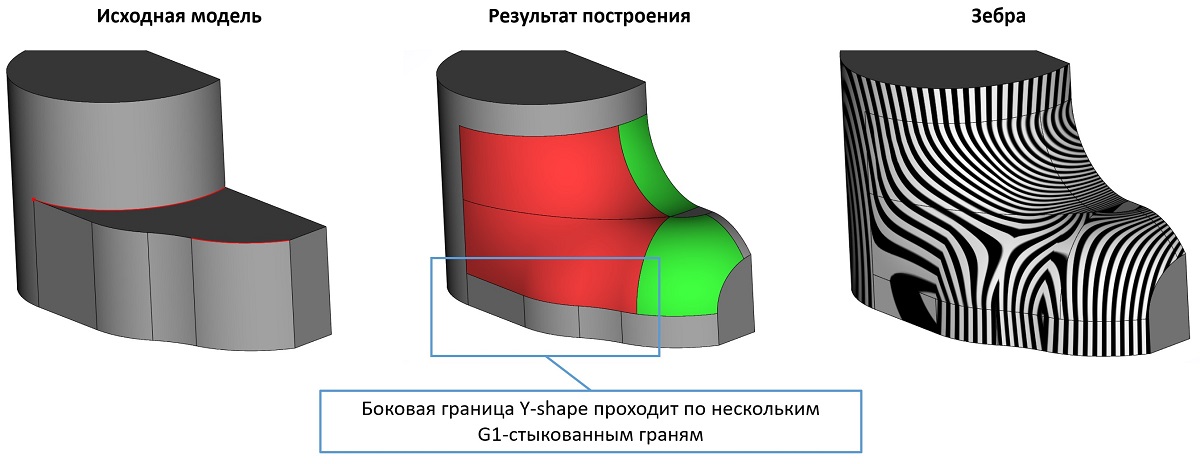
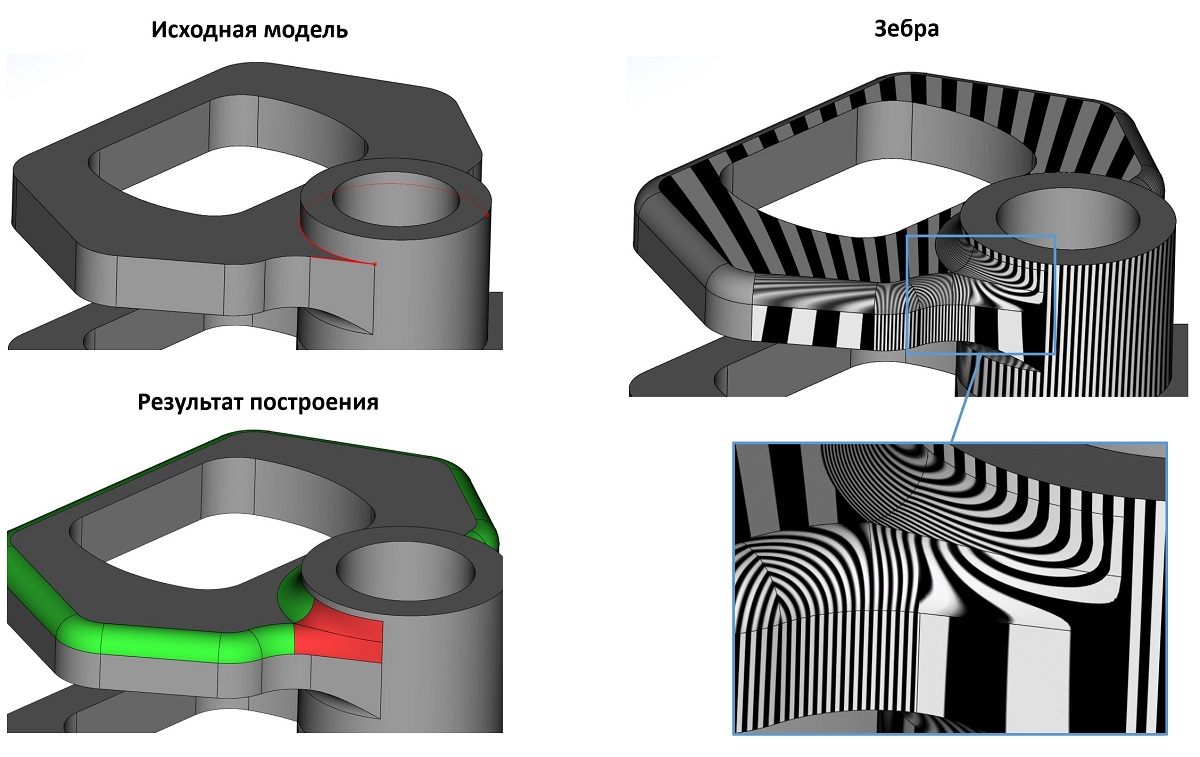
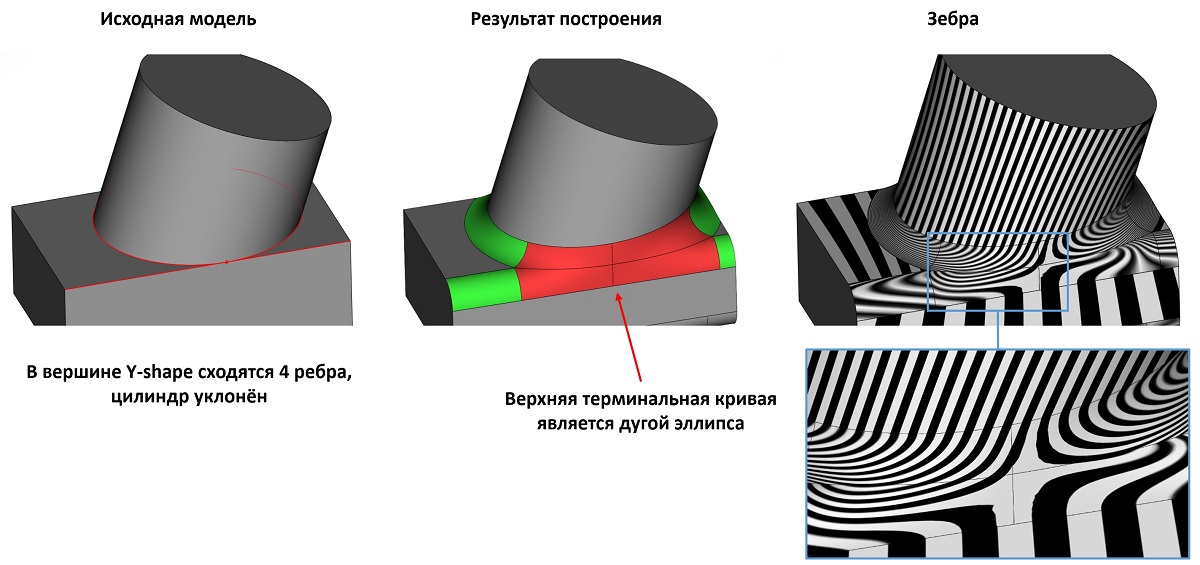
Примеры работы Y-формы в новой версии ядра
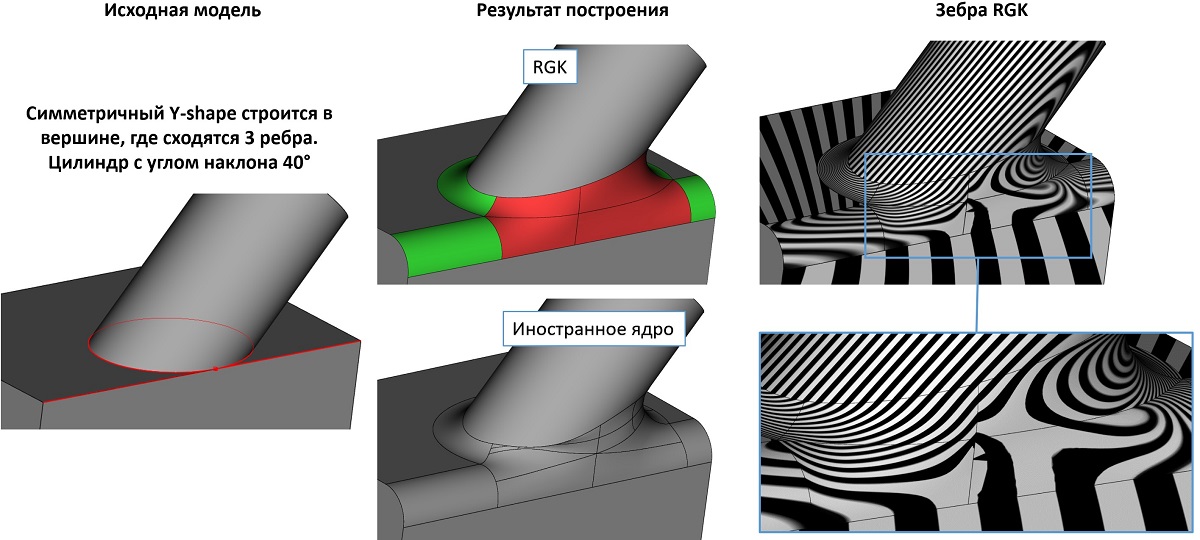
Иллюстрация сравнения поведения алгоритма Y-формы с известным иностранным конкурирующим ядром
Примеры выше приведены, в частности, для иллюстрации того, насколько кропотливо и ответственно подходит команда RGK к отработке принципиальных вопросов в математике ядра, в силу понимания особой значимости аспектов качества конечных моделей в приложениях.
Как отмечалось, изменения затронули не только геометрические аспекты сглаживания, но и даже в большей степени возможности топологического алгоритма. Если возможности Y-формы — это функциональность на стыке геометрии и топологии, то, например, возможности построения составной заплатки — это больше логика управляющего алгоритма топологического свойства.
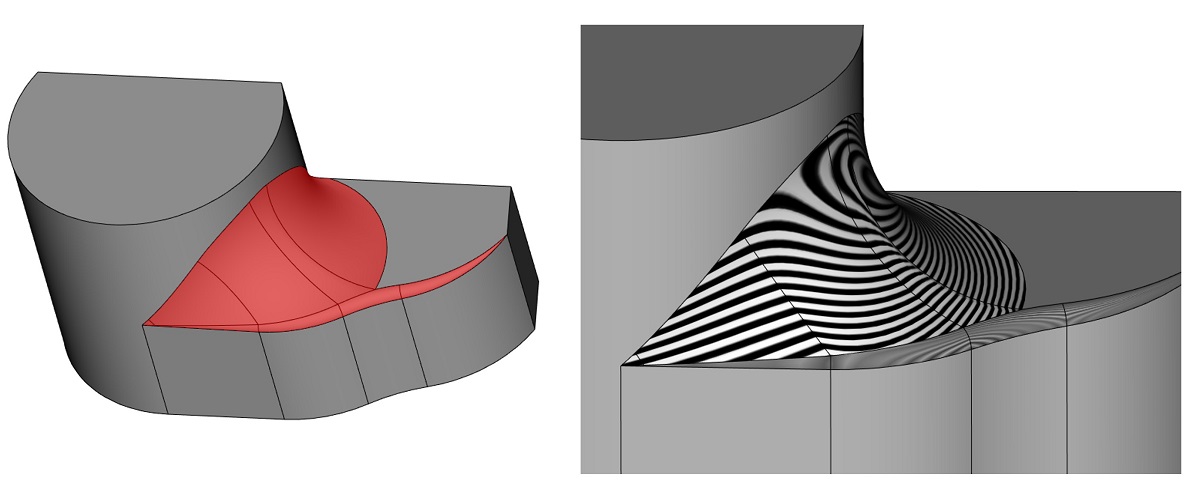
Иллюстрация поддержки многосегментной «заплатки» в алгоритмах сглаживания переменного радиуса
Много внимания было уделено улучшению надёжности алгоритмов с учётом точностей исходных моделей.
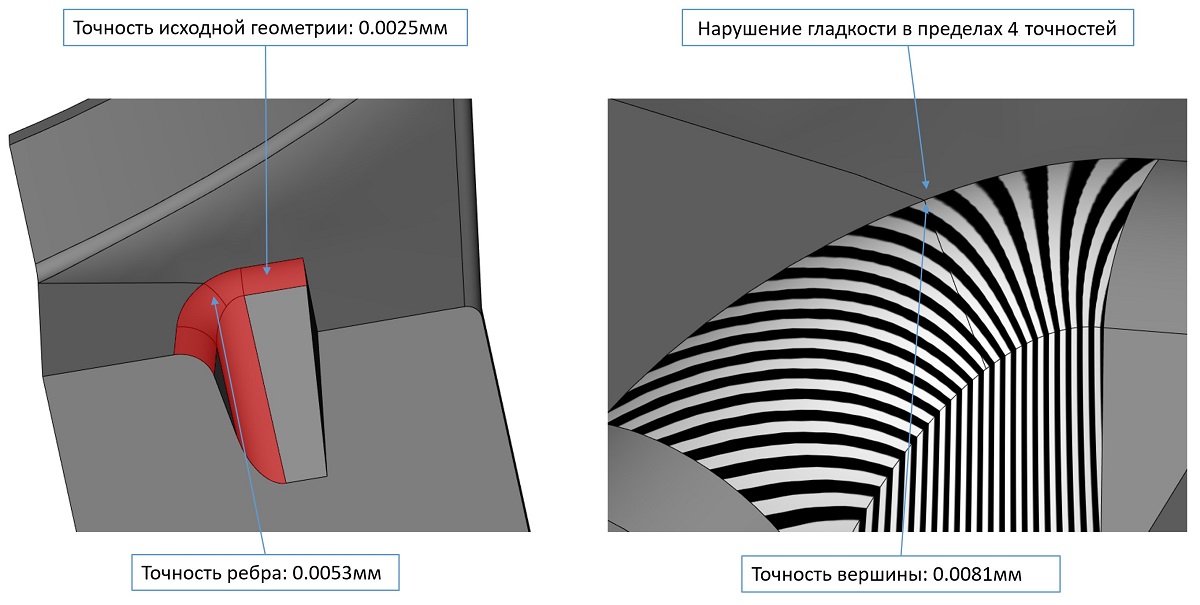
Пример обработки через «почти касательное» ребро с корректировкой фактической точности топологии
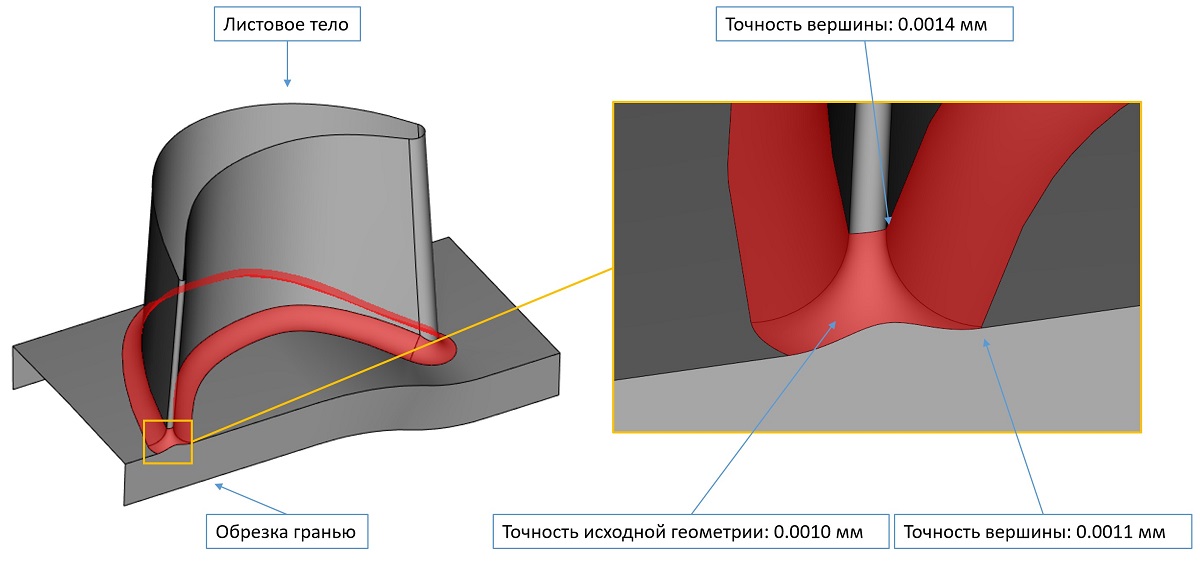
Иллюстрация учёта точности входной геометрии в ситуации обрезки боковой гранью
Также был снят ряд ограничений в алгоритмах перекрытия сглаживающих последовательностей. Вот несколько примеров, которые теперь обрабатываются новой обобщённой логикой.
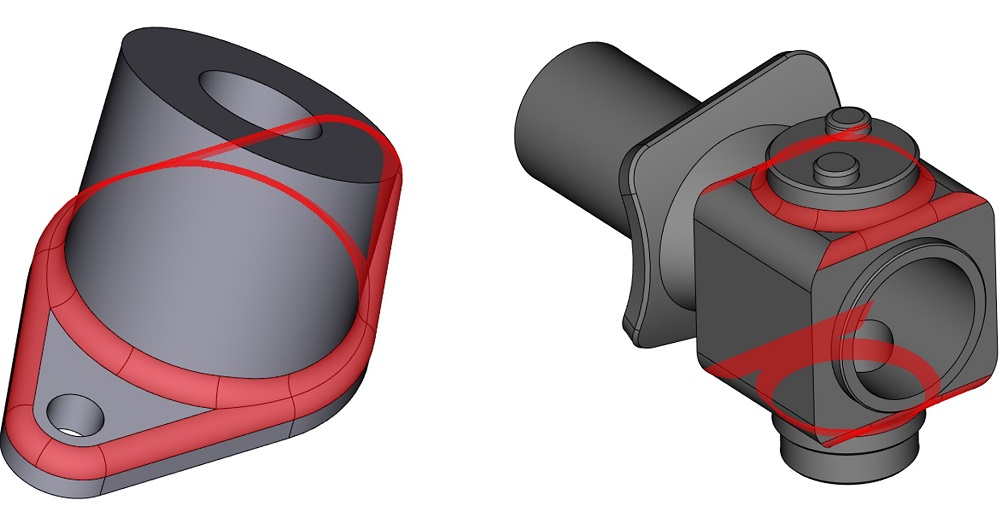
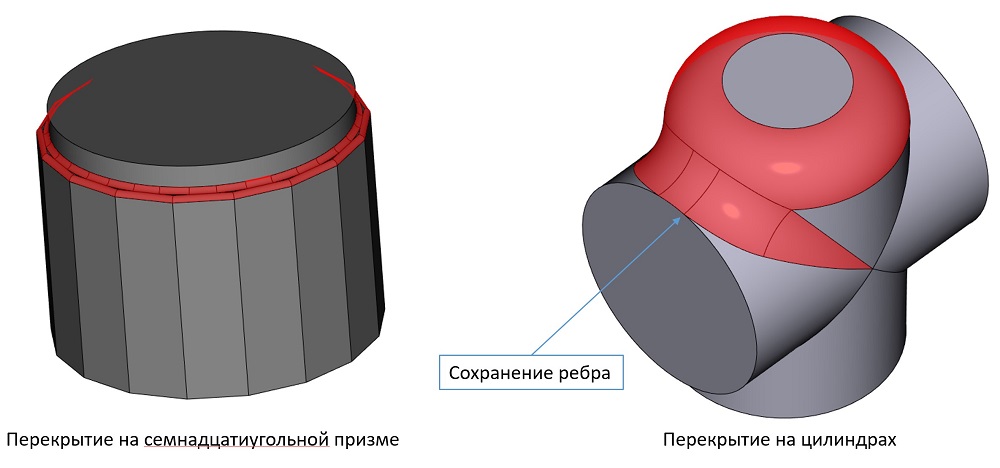
Примеры перекрытия сглаживающих последовательностей (построение сглаживания за одну операцию)
Ослаблены ограничения в топологии трёх- и четырёхрёберных обработок, сходящихся в одну вершину рёбер.
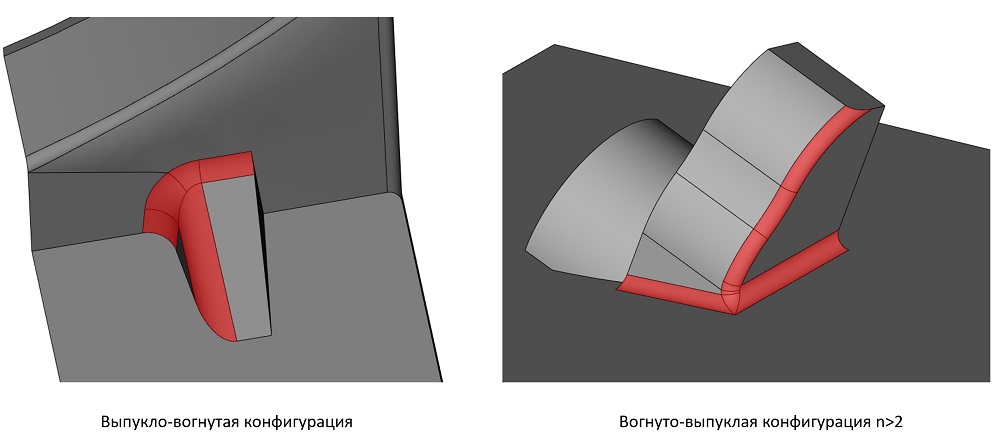
Иллюстрация новых возможностей RGK в «трёхрёберной» обработке
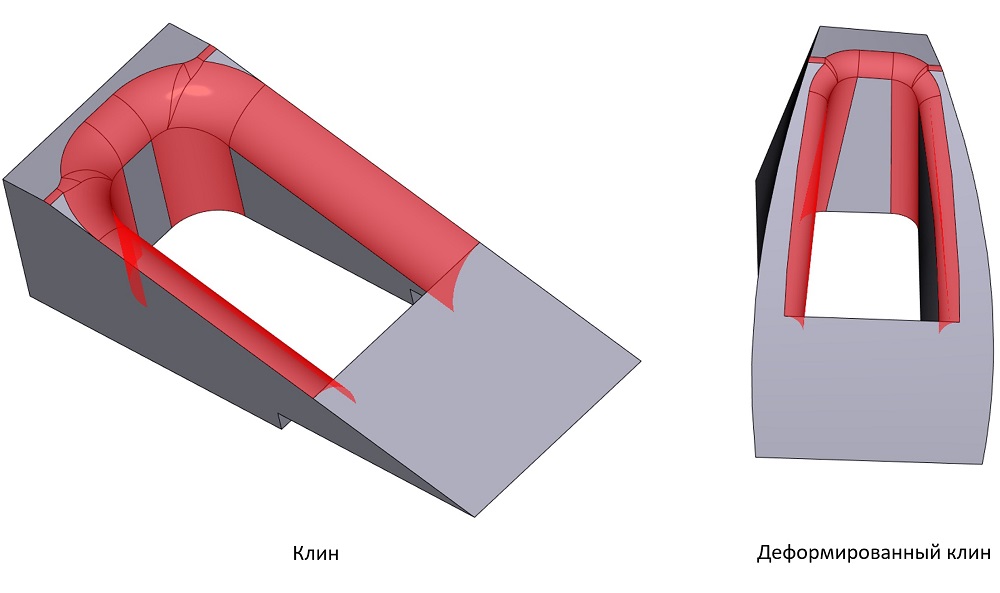
Иллюстрация возможностей «четырёхрёберной» обработки (тело справа с аналитическими поверхностями, а слева тело той же топологии, но со сплайновыми гранями и более грубой точностью топологии)
Рассмотрим ещё ряд улучшений топологических алгоритмов сглаживания. Нередко возникают ситуации, когда сглаживаемые грани в одной своей области трансверсальны, а в другой практически касаются друг друга. Бывают также ситуации, когда конфигурации граней имеют так называемую «переменную» выпуклость — одна часть выпуклая, а другая вогнутая. Такие случаи являются вызовом для любого геометрического ядра. Если ещё добавить, что сглаживаемые рёбра могут иметь разные точности, то становится понятно, что стоит задача корректного учёта как входных точностей модели, так и особенностей задачи с «неприятной» постановкой, о которых мы писали в начале статьи. Теперь несколько наглядных примеров того, что умеет новая версия RGK.
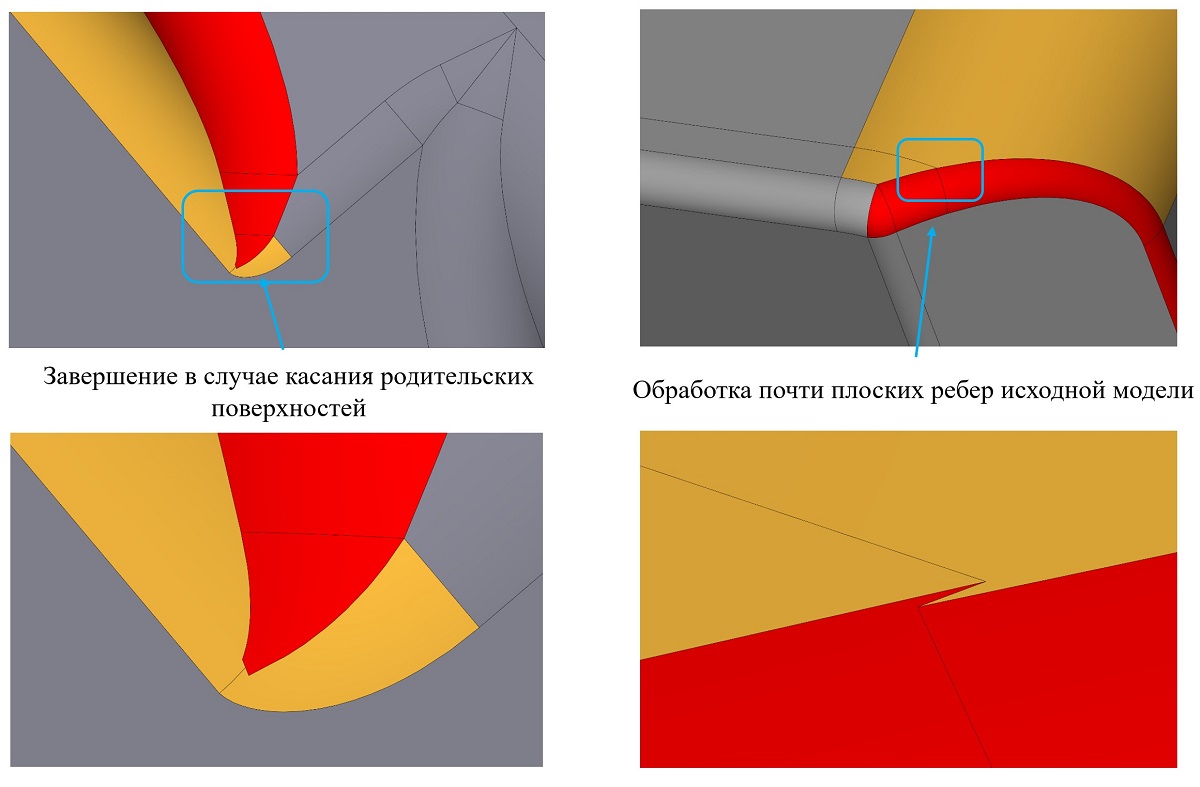
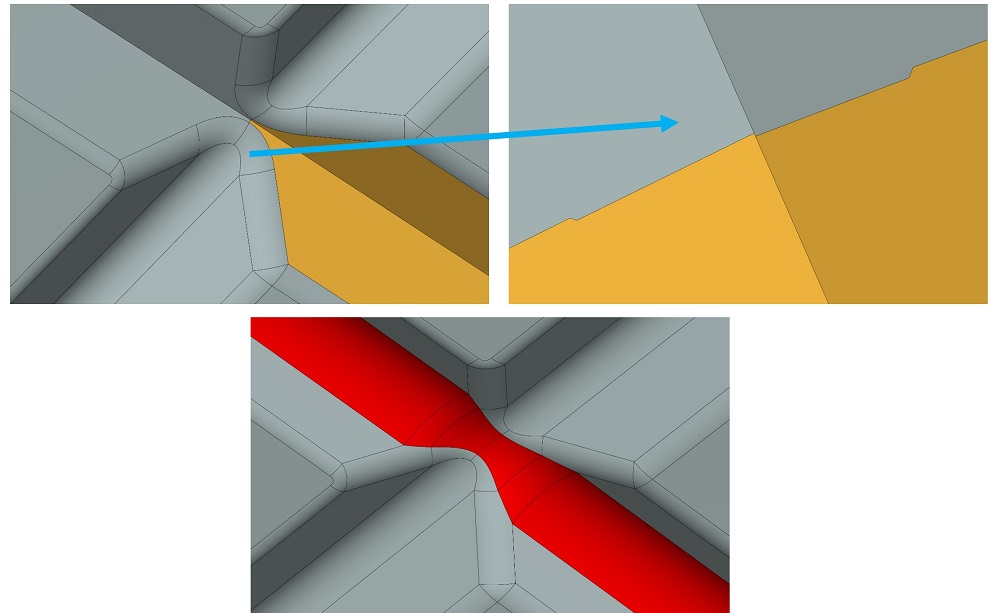
Примеры работы RGK в областях с «неприятной» структурой
Примером задачи такого рода является сглаживание с касанием листов сглаживания или выходом на границы граней. То есть ситуации, когда ещё нет переполнения и корректировки геометрии сглаживающей поверхности в связи с изменением опорной геометрии, но сглаживаемая грань уже перекрывается сглаживанием полностью или частично. В этой ситуации тоже надо понимать, что точности рёбер, которые становятся границей сглаживания, могут быть разными.
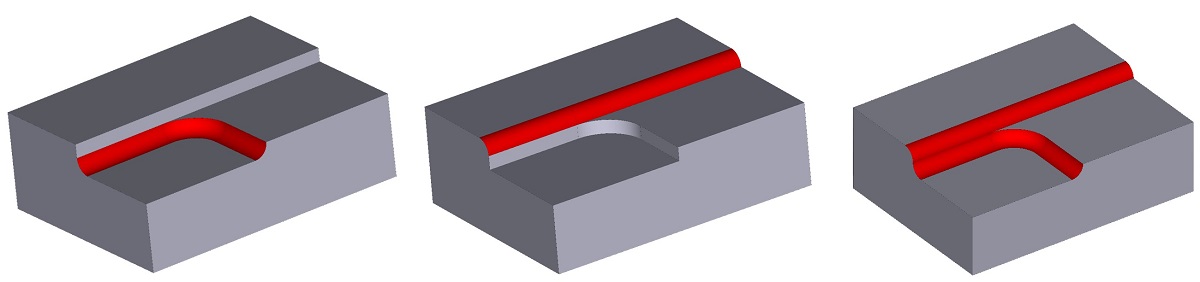
Пример корректной работы алгоритмов RGK новой версии в «пограничных» случаях (приведён случай на фрагменте реальной модели, где сглаживаемые грани представляют собой сплайновые поверхности)
Дальнейшей доработке подвергся механизм встраивания сглаживающих листов в тело. Теперь он позволяет строить модели с конфигурацией топологии, доступные не всем системам так называемого «тяжёлого» класса.
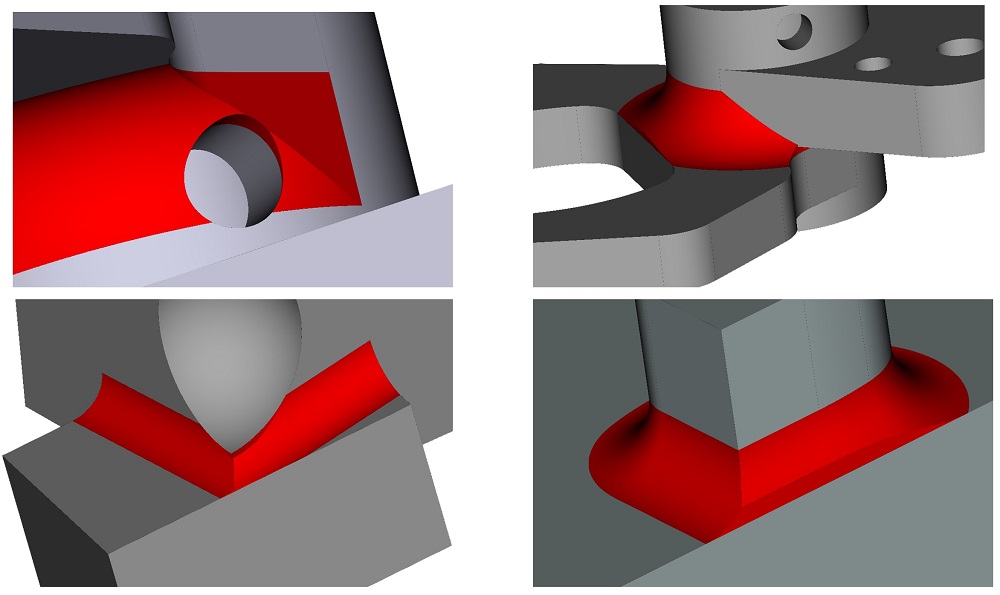
Примеры работы нового алгоритма встраивания сглаживания
Также развитие получила функциональность по остановке сглаживания по требованию, которая была представлена в предыдущих версиях. Сейчас функциональность стала значительно более мощной.
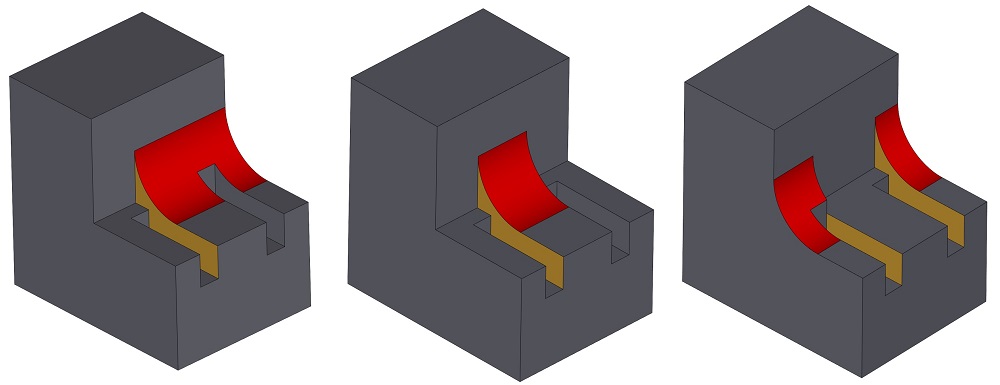
Пример работы функциональности остановки сглаживания по выбранной топологии тела
Реклама. АО «Топ Системы» ИНН 7726601967. erid: 2SDnjcGZcKw