В статье речь идёт об овале, созданном с использованием одного технического приёма выдающегося английского (шотландского) физика, математика и механика Джеймса Максвелла, но без применения устройства, предложенного им для этого (рис. 1). Построение и изучение овала показало отсутствие тождественности его очагов (центров построения) и фокусов, а также позволило установить и некоторые другие его свойства.
Рис. 1
— Скажите государю, что у англичан ружья кирпичом
не чистят: пусть чтобы и у нас не чистили…
Просматривая в Интернете материалы по овальным кривым, встретил упоминание о многофокусных кривых, которые строил Джеймс Максвелл. Интересно было узнать об этих кривых и о том, как они строятся. Прочитал в Википедии статью о Максвелле, из которой узнал, что он, в возрасте четырнадцати с половиной лет придумал способ рисования овалов. Вот цитата из статьи: «Этот метод, восходивший к работам Рене Декарта, состоял в использовании булавок-фокусов, нитей и карандаша, что позволяло строить окружности (один фокус), эллипсы (два фокуса) и более сложные овальные фигуры (большее количество фокусов). Эти результаты были доложены профессором Джеймсом Форбсом на заседании Эдинбургского королевского общества и затем опубликованы в его «Трудах»…».


Удалось также разыскать несколько рисунков Максвелла с этими овалами. При рассмотрении рисунков возникло предположение, что информация об этих овалах, ранее полученная мной, не точна, поскольку на рисунках изображены центры построения кривых, а не фокусы. Сомнительным также показался термин в Википедии: «булавок-фокусов», поскольку в совпадение центров построения с фокусами (за исключением окружности и эллипса) абсолютно не верилось.
В Интернете же нашёл первое упоминание о статье Максвелла:1846 Maxwell’s first paper “On the description of oval curves and those having a plurality of foci” Proc Roy Soc Edinburgh, Vol. II (1846 Первая публикация Дж.Максвелла «К описанию овальных кривых и кривых с множественными очагами»). Обратите внимание – Максвелл говорит не о фокусах.
Чтобы окончательно разобраться в этом, принято решение построить один из овалов, созданных ранее Максвеллом. Я уже готов был подыскивать для макета подходящий лист толстого картона, булавки и нитки, но, остановила мысль – как же тяжело будет потом вручную (без компьютера) отыскивать фокусы кривой. А нельзя ли обойтись без «хитроумного» устройства Максвелла? И это удалось сделать, причём, не выходя из компьютера, но только после того, как был разгадан небольшой секрет М., который заключался в определённой трассировке нити (см. рис. 2).
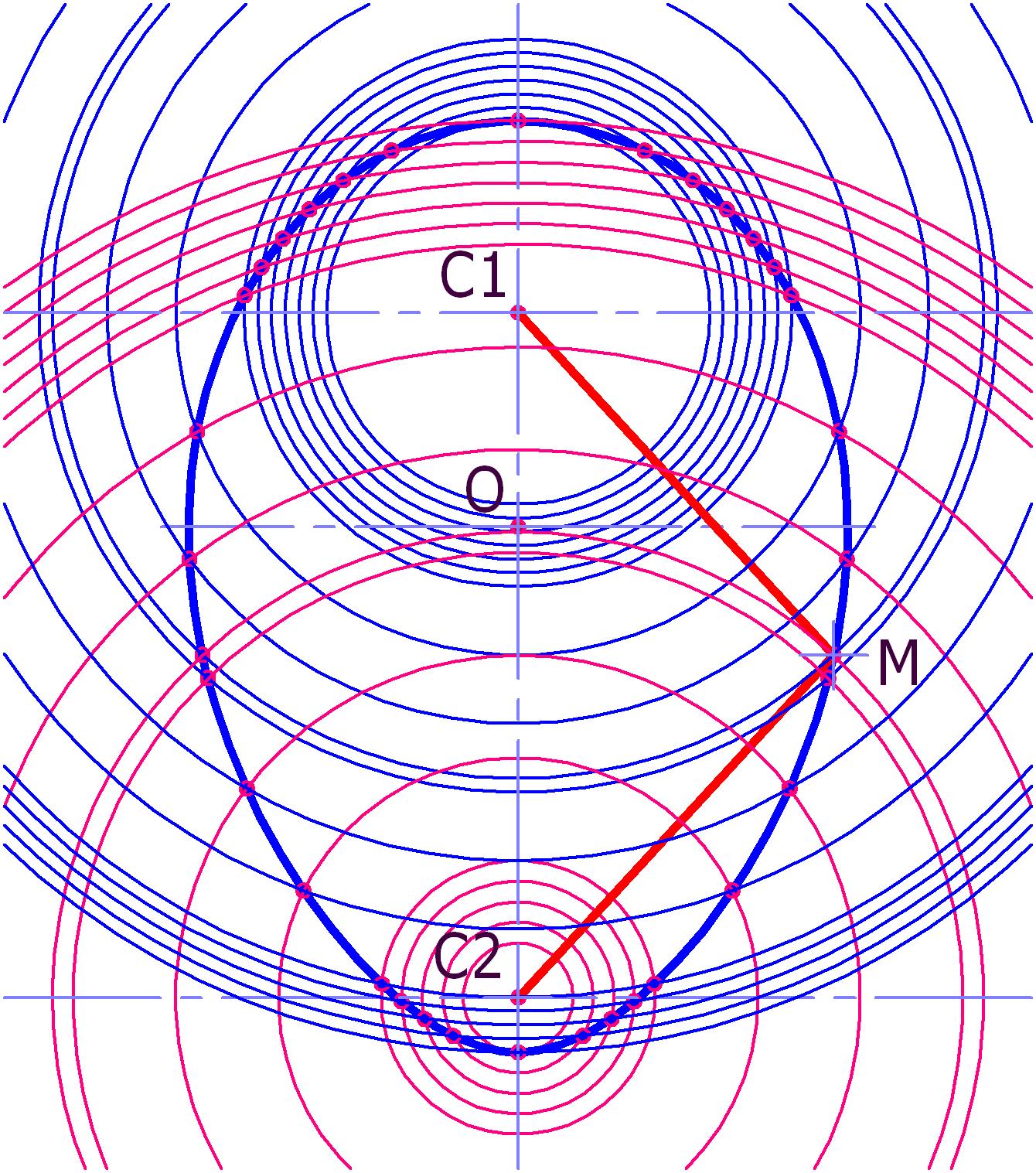
Рис. 2
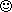
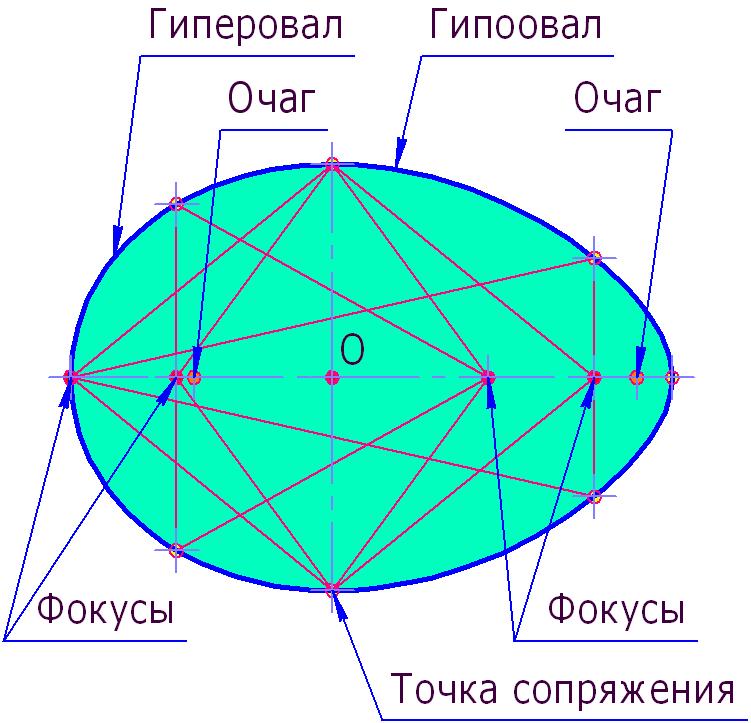
Рис. 3
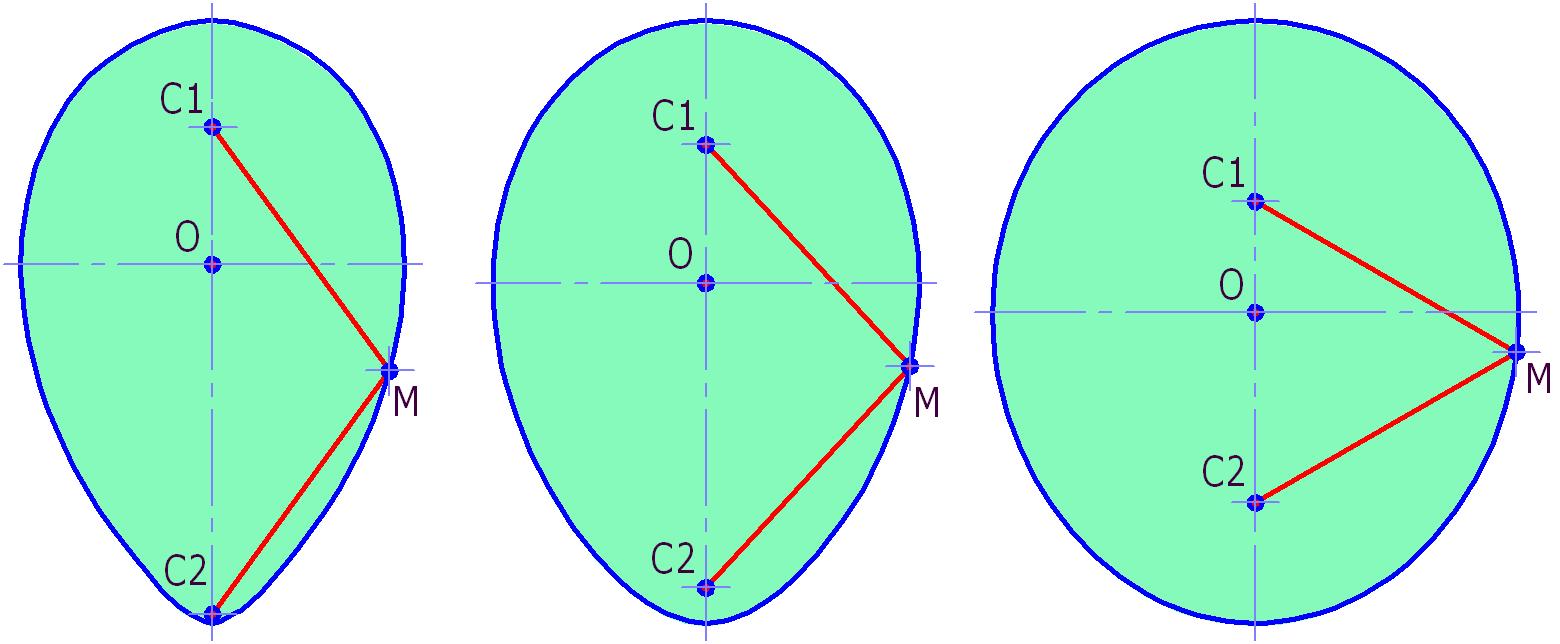
Рис. 4
Овалы с числом центров построения 3…5 пока я не рассматривал, как ведут себя фокусы у них, есть ли они вообще, и сколько их, возможно, посмотрим позднее.
Задача оказалась не только интересной и познавательной, но и полезной для тренировки «серого вещества», по крайней мере, для меня, так что, рекомендую поупражняться с ней, лучше утром, когда мозг свеж. Думаю, что булавки и нить для этого вам, как и мне, не понадобятся, хотя с ними тоже интересно позаниматься, поверьте Джеймсу Максвеллу!