

Игорь Батюченко — руководитель группы разработки ЗАО «Топ Системы».
Изделия сложных форм
Поверхностное моделирование применяется при проектировании широкого спектра промышленных изделий со сложной формой: от бытовой техники и автомобилей до летательных аппаратов и морских судов. Одним из подходов данного типа моделирования является использование набора опорных профилей и обводных кривых, на основе которых строятся поверхности перехода.Однако зачастую использование стандартных операций для создания подобного рода геометрии бывает неудобным и по затраченному времени не слишком эффективным. При решении задач построения поверхностей с заданными характеристиками конструкторам необходимо использовать единый инструмент, позволяющий выбирать различные варианты задания исходных данных (например поверхности конического сечения). Поэтому нами был создан механизм построения подобного рода поверхностей с общим набором свойств там, где это допустимо.
Переходные поверхности
В T-FLEX CAD 17 операция, включающая в себя семейство поверхностей конического сечения, имеет обобщённое название Переходная поверхность. Назначение операции: создать поверхность перехода между двумя другими поверхностями (в своем большинстве), имеющую определённые граничные условия, а также конкретную, хотя, возможно, и переменную по «длине», форму поперечного сечения (более подробно об этом далее).В настоящее время операция имеет в своем арсенале десять способов построения, разделенных на три группы по типу сечения:
- коническое, 4 типа;
- окружность (дуга), 4 типа;
- прямая, 2 типа.
В данной статье мы рассмотрим поверхности конического сечения. И хотя все способы имеют схожий механизм построения, для получения результирующей поверхности в каждом случае необходимо задавать свой набор начальных данных. Например, для построения поверхности с типом сечения «окружность» обязательно задание осевой кривой (но не обязательно прямой линии).
В основе построения поверхностей конического сечения лежат четыре типа алгебраических кривых второго порядка, полученных в результате сечения конуса плоскостью (вырожденные случаи не рассматриваются): эллипс, окружность (как частный случай эллипса), парабола и гипербола. Однако особенностью данных поверхностей является отсутствие необходимости явного указания формы сечения. Определение типа кривой происходит автоматически на основе входных управляющих параметров. Но всё-таки, во-первых, где можно найти эти самые кривые в результирующей поверхности, а во-вторых, как узнать, кривая какого типа лежит в основе её (поверхности) построения?
Ответ на первый вопрос состоит в следующем. Опорная кривая – первое и, пожалуй, ключевое поле, которое видит пользователь при запуске операции. Она есть во всех десяти способах построения. Два основных свойства Опорной кривой:
- если в любом произвольном месте (точке) данной кривой построить плоскость, перпендикулярную этой кривой, а затем пересечь ее с результирующей поверхностью – получим то самое коническое сечение (рис. 1, пунктирные линии);
- она определяет максимальную «длину» результирующей поверхности (рис. 1).

Рис. 1. Поверхность конического сечения по изогнутой опорной кривой
Где и как расположены кривые второго порядка, которые являются основным «скелетом» (базовыми профилями) результирующей поверхности, выяснили. Осталось узнать, как можно управлять формой поверхности (то есть типом и формой самих кривых). Для этого доступны четыре варианта. Рассмотрим первые два из них:
- Дискриминант – вещественное число в диапазоне (0; 1). Геометрический смысл показан на рис. 2 (сечение перпендикулярно опорной кривой). При значениях (0; 0.5) – эллипс; 0.5 – парабола; (0.5; 1) – гипербола. В случае симметрии при значении 0.4142 (корень из двух минус один) – окружность.
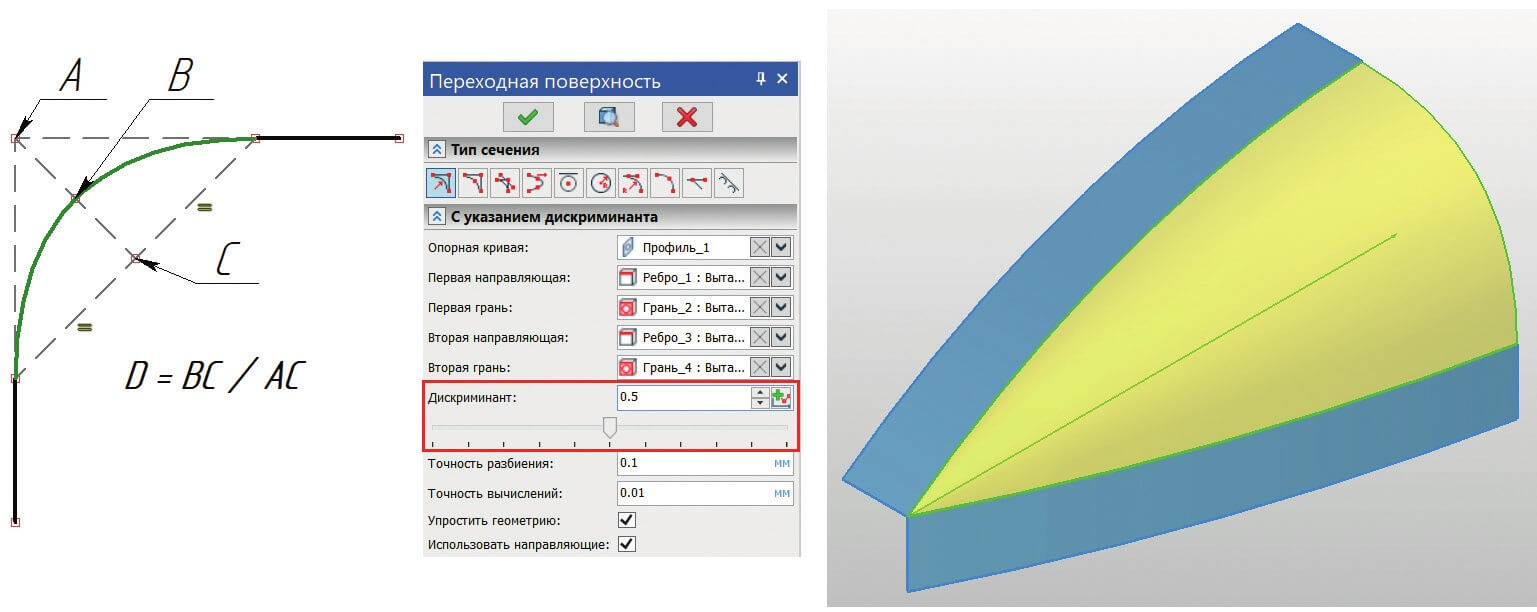
Рис. 2. Определение инженерного дискриминанта и поверхность, начинающаяся в точке (А – точка пересечения касательных на концах граней; АС – медиана треугольника)
- Промежуточный путь – пользователь должен указать промежуточную кривую, через которую в итоге и пройдет результирующая поверхность. Главной особенностью этой кривой является тот факт, что в каждом перпендикулярном сечении вдоль опорной кривой точка пересечения её и плоскости должна лежать строго внутри треугольника, изображённого на рис. 3 (треугольник ABC).
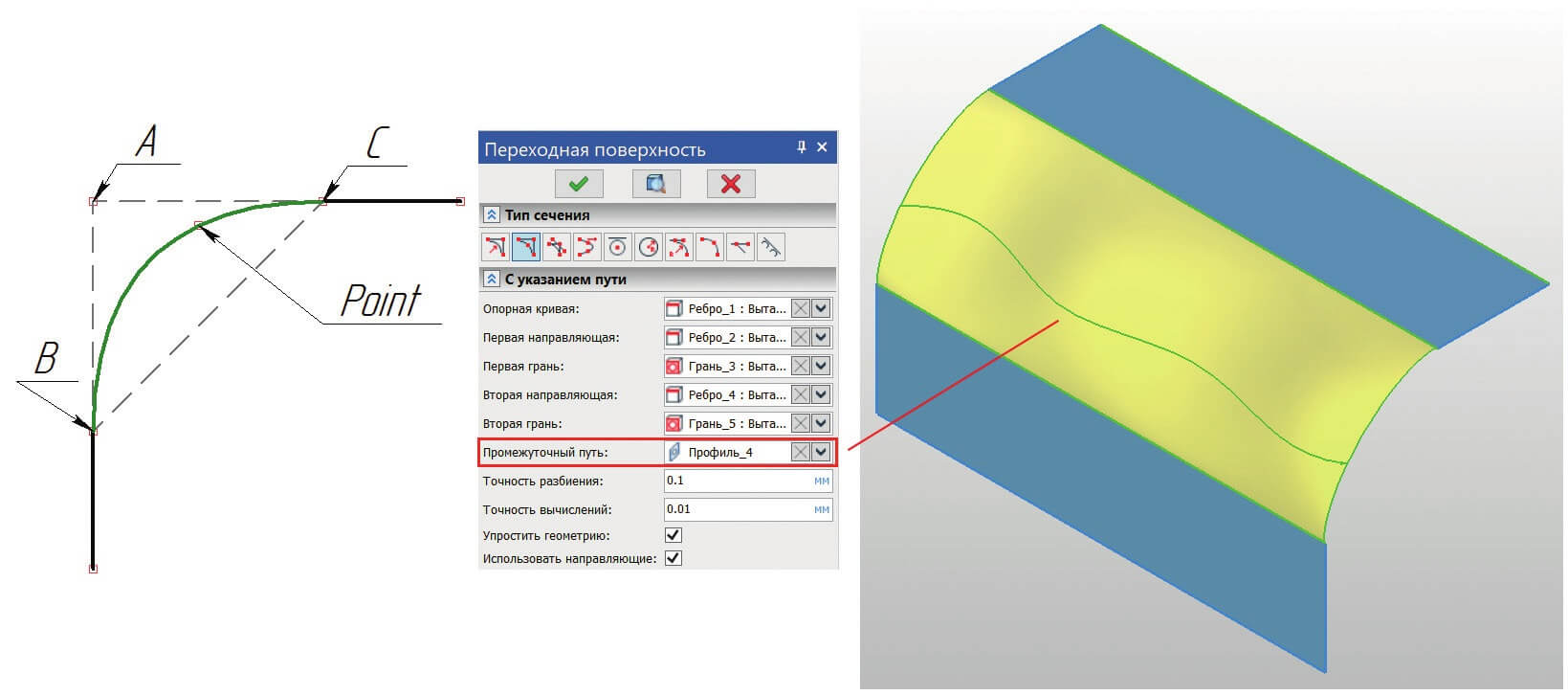
Рис. 3. Условие построения и поверхность через промежуточный путь в форме сплайна (Point – точка пересечения перпендикулярной плоскости и промежуточного пути)
Во всех полях данной операции, где нужно вводить числовые значения (константу), можно подключить график и сделать соответствующие значения переменными по длине опорной кривой. На выбор доступны три типа графика: «Полилиния» – односвязный набор прямых отрезков; «Кубический сплайн» – кривая с возможностью задания касательных условий для каждого узла; «По 3D кривой» – нужно указать две кривые из документа, описывающие закон изменения параметра.
Таким образом, задав переменное значение дискриминанта с помощью графика (например выбрав тип «кубический сплайн»), получим поверхности, различные не только по форме, но и по типу сечения вдоль опорной кривой – от эллипса до гиперболы (рис. 4).
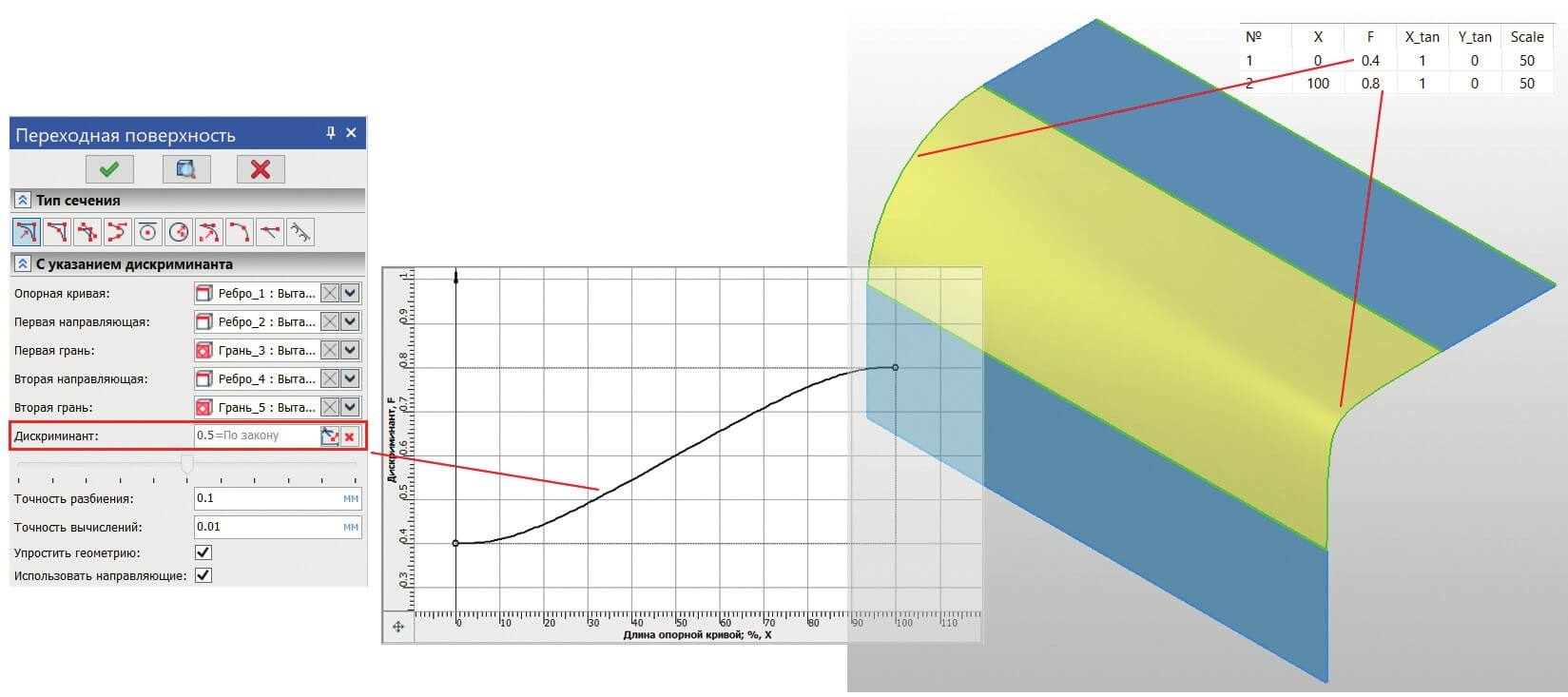
Рис. 4. Поверхность, заданная графиком дискриминанта в диапазоне (0.4; 0.8)
Данный тип поверхности является ключевым для многих инженерных отраслей, в частности аэрокосмической. При проектировании авиационной техники поверхность конического сечения – одна из самых часто встречающихся операций в дереве построения. Именно поэтому на данном этапе разработки системы мы вынесли в интерфейсную часть чуть больше «ручек» по настройке результирующей поверхности.
Линейчатые поверхности
Линейчатая поверхность – поверхность, образованная движением прямой линии. Прямая при этом называется прямолинейной образующей, а движется в пространстве она вдоль направляющих кривых. Чтобы не запутаться, не будем «жонглировать» названиями таких поверхностей (геликоид, гиперболоид и т. д.), получаемых различными вариациями образующих и направляющих кривых. Просто рассмотрим два варианта построения:
- одна из направляющих кривых – точка;
- заданы обе направляющие кривые (рис. 5).
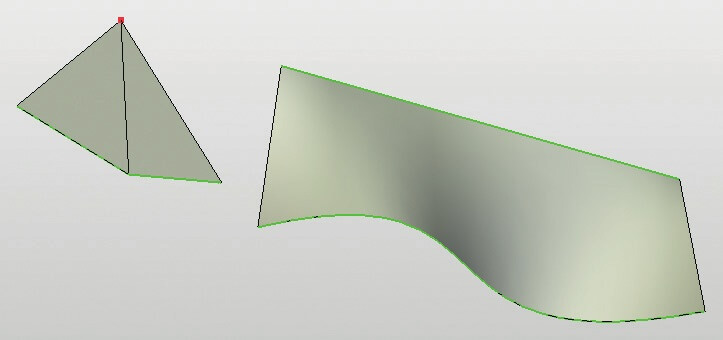
Рис. 5. Примеры линейчатых поверхностей (зелёные линии — направляющие)
На первый взгляд, всё довольно просто и понятно, особенно по сравнению с поверхностями конического сечения. Прямая – это алгебраическая кривая первого порядка, на порядок ниже кривых конического сечения. Зачем нужны данные поверхности и где они применяются? Множество примеров использования встречается в архитектуре. Шуховская башня в Москве – сетчатая конструкция в форме линейчатого гиперболоида. Балки являются прямолинейными образующими для каждой секции. Еще один интересный пример: хотя в это трудно поверить, но форму «чипсов из тубуса» тоже можно повторить движением прямой (гиперболический параболоид).
Вернемся к одноименной операции Линейчатая поверхность в T-FLEX CAD 17. Первый тип построения (когда в качестве первой направляющей указана точка) довольно прост и имеет минимум особенностей и ограничений. Рассмотрим случай, когда заданы обе направляющие кривые.
Способ построения поверхности методом, описанным в теории, звучит вполне разумно: нужно создать прямой профиль и «протолкнуть» его вдоль жестких рамок в виде направляющих кривых. Но если учесть, что эти самые направляющие могут быть совершенно разной формы, длины или даже иметь изломы (составной путь), то возникает целый ряд вопросов, главный из которых – согласно какому закону должно выполняться движение прямой образующей? В результате был выбран совершенно иной механизм получения результирующей поверхности.
Вместо того чтобы проталкивать линейный профиль вдоль направляющих кривых, можно использовать эти самые кривые в качестве двух сечений. Именно поэтому в диалоге операции первые два поля имеют названия «Первое сечение» и «Второе сечение» соответственно. Условно, соединив по прямой линии каждую точку первой кривой со второй, мы и получим линейчатую поверхность. Остается лишь определиться с «законом», согласно которому будет выполняться выравнивание (распределение) UV‑кривых в результирующей поверхности. На момент публикации доступны два варианта.
По длине дуги
Используется полная длина выбранных сечений. Суть выравнивания и пример поверхности показаны на рис. 6.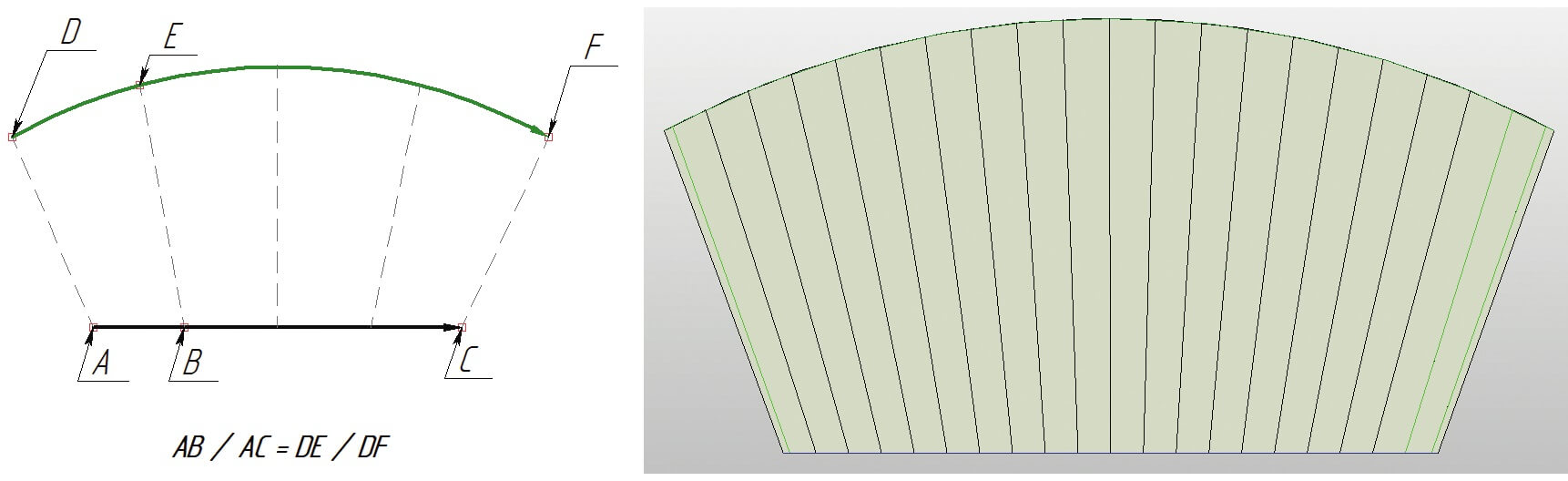
Рис. 6. Распределение изопараметрических линий (тип выравнивания – по длине дуги)
По опорной кривой
Границы поверхности определяются длиной и формой опорной кривой. Её смысл аналогичен операции Переходная поверхность. Именно в перпендикулярных сечениях к опорной кривой и будут располагаться прямые изопараметрические линии поверхности (рис. 7).
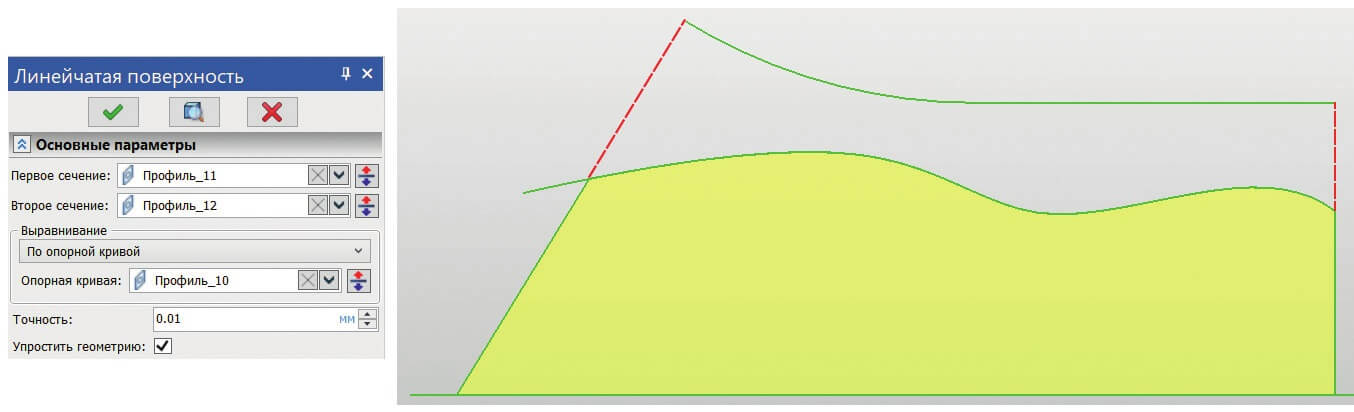
Рис. 7. Линейчатая поверхность по опорной кривой
В заключение стоит сказать, что оба режима поддерживают возможность создания поверхности между двумя замкнутыми контурами, которые, в свою очередь, могут иметь различное число рёбер и вершин (рис. 8). При этом сохраняется исходная геометрия сечений (создается несколько поверхностей в рамках одного тела).
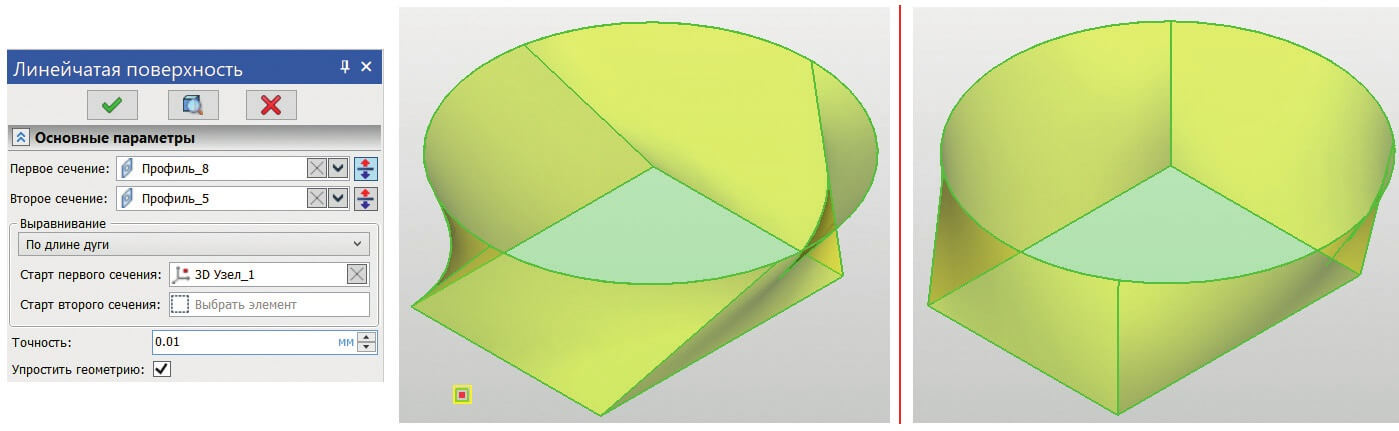
Рис. 8. Поверхности «по длине дуги» и «по опорной кривой»
Продолжение по закону
Операции с подобным названием создаются для определенных целей: в продолжение исходной грани, перпендикулярно выбранному ребру создать новую поверхность (в качестве образующего профиля чаще используется прямая или дуга окружности). Однако в случае с операцией Продолжение по закону мы получили одну из самых нестандартных возможностей, выходящую за рамки создания поверхностей, – при необходимости можно получить твердотельную геометрию с широким набором свойств, необходимых для управления её формой и габаритами.
Доступно два варианта продолжения.
Дугой окружности
Цель – создать новую поверхность в продолжение выбранной грани (в качестве профиля – дуга окружности). Но в каком направлении? Самое очевидное решение, что «продолжать» нужно перпендикулярно выбранному ребру. Однако возможны ситуации, когда это не является ожидаемым решением. На выбор доступен вариант Изопараметрически. В таком случае продолжение будет по касательной к изопараметрическим кривым грани в каждой точке выбранного ребра (рис. 9).
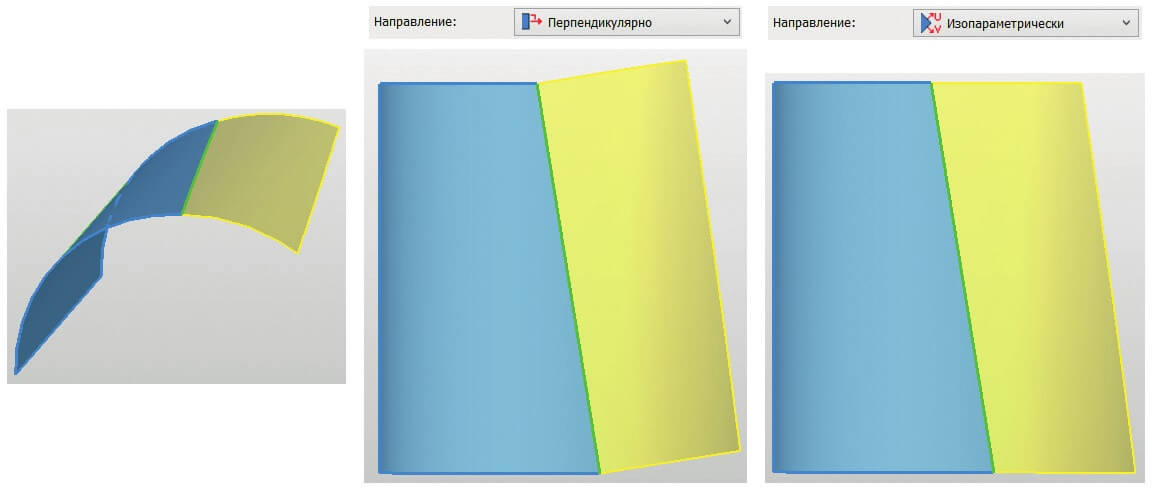
Рис. 9. «Продолжение» обрезанного ребра цилиндрической грани
Помимо выбора направления доступен выбор и граничных условий: «G1» (непрерывность по первой производной) и «G2» (непрерывность по второй производной – кривизне). В первом варианте радиус кривизны указывается в явном виде. В случае выбора условия «G2» радиус высчитывается автоматически. Особенностью данного условия является то, что вычислять нужно не радиус кривизны ребра в его точке, а радиус кривизны поверхности в заданном направлении (в этой же точке ребра). Если же кривизна в заданном направлении изменит свой знак, то результирующая поверхность в этом месте будет изгибаться в другую сторону (рис. 10).
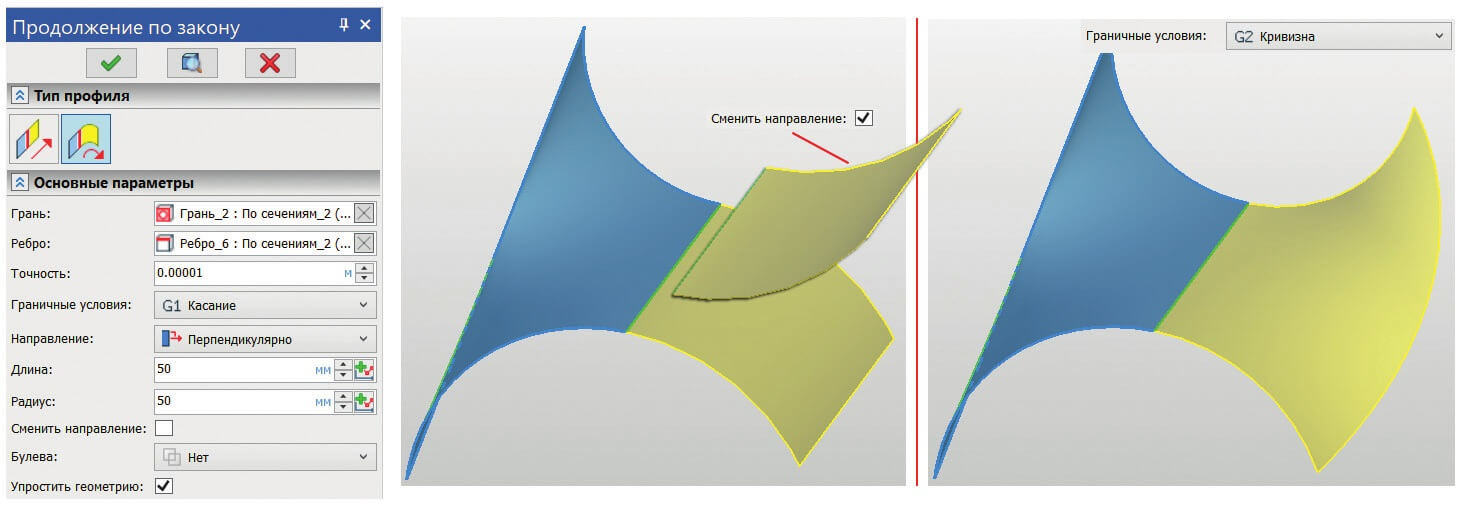
Рис. 10. Два варианта «продолжения» для условия «G1» и один для условия «G2»
Также стоит сказать, что для полей задания радиуса и длины доступно подключение графиков.
Линейным профилем
Для начала рассмотрим данный вариант в контексте построения новой поверхности. Выбрав исходную грань, в отличие от типа профиля в форме дуги окружности, можно указать сразу несколько ребер, которые мы хотим «продолжить». При этом выбранные ребра не обязательно должны образовывать один гладко сопряжённый путь (могут и вовсе не иметь общих вершин). То есть два соседних ребра могут соприкасаться под любым углом. В этом случае на выбор доступны три варианта обработки таких «изломов»: разделить, продлить или скруглить (рис. 11).
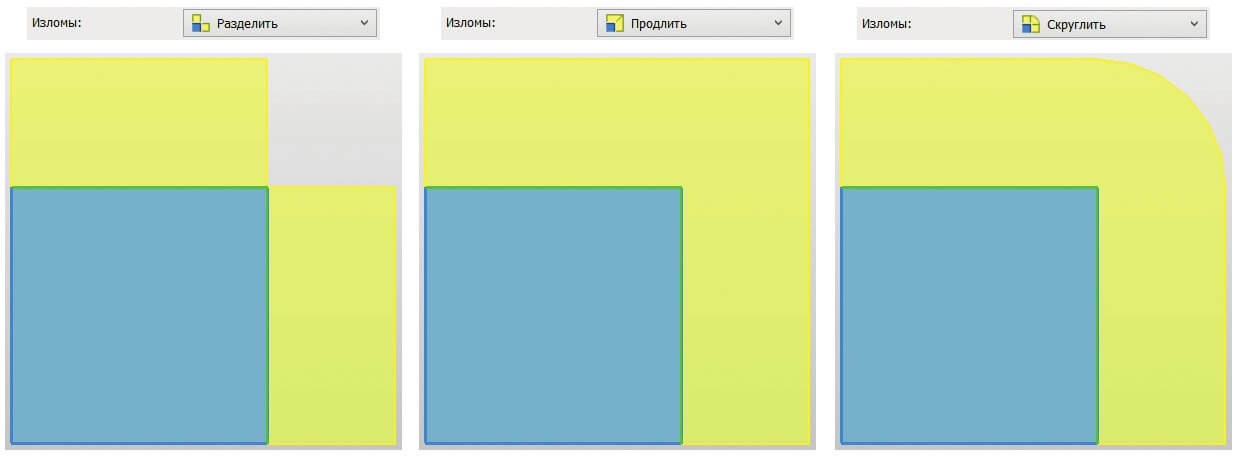
Рис. 11. Три типа обработки изломов для поверхностей
Другое назначение данной операции – моделирование фрезерной обработки (цилиндрического сечения). Хотя, конечно, имея «под рукой» широкий функционал в одной операции, использовать её можно в различных целях. Описание всех возможностей займёт довольно много времени и места, поэтому далее рассмотрим только пример с фрезерованием.
Всё, что нам нужно, – это сама твердотельная модель и набор проволочных объектов (принадлежащих одной из её граней), имитирующих путь, по которому должна пройти ось фрезы. Задав соответствующие исходные данные, вначале мы получаем новую поверхность (рис. 12), по сути, такую же, как и в случае, когда мы просто «продолжали» грань.

Рис. 12. Шар с различными типами профилей
Далее устанавливаем нужные параметры:
- Направление: нужно установить значение Симметрично или Разная и указать соответствующую глубину обработки. В данном случае нельзя выбирать только одно направление, так как при последующих булевых операциях в случаях с неплоскими гранями исходного тела образуются так называемые «невалидные контакты»;
- Толщина: так как мы условились, что выбранные направляющие являются осевой линией для фрезы, выбираем значение Симметрично (рис. 13, слева);
- Сглаживание: обработка концов (а именно начала и конца) нового тела. Устанавливая значение Грани, получаем полное сглаживание торцевых граней (рис. 13, в центре);
- Изломы: смысл данной опции при работе с твердотельной геометрией отличается от случаев, когда в результате получаем поверхность. Теперь она работает в связке с опцией Сглаживание и означает то, как именно следует обрабатывать внешние углы в местах изломов. При выборе значения Скруглить радиус скругления высчитывается автоматически, исходя из выбранной опции в Сглаживании и значения Толщины (рис. 13, справа);
- Булева: заключительная часть создания операции. Устанавливаем значение Вычитание.
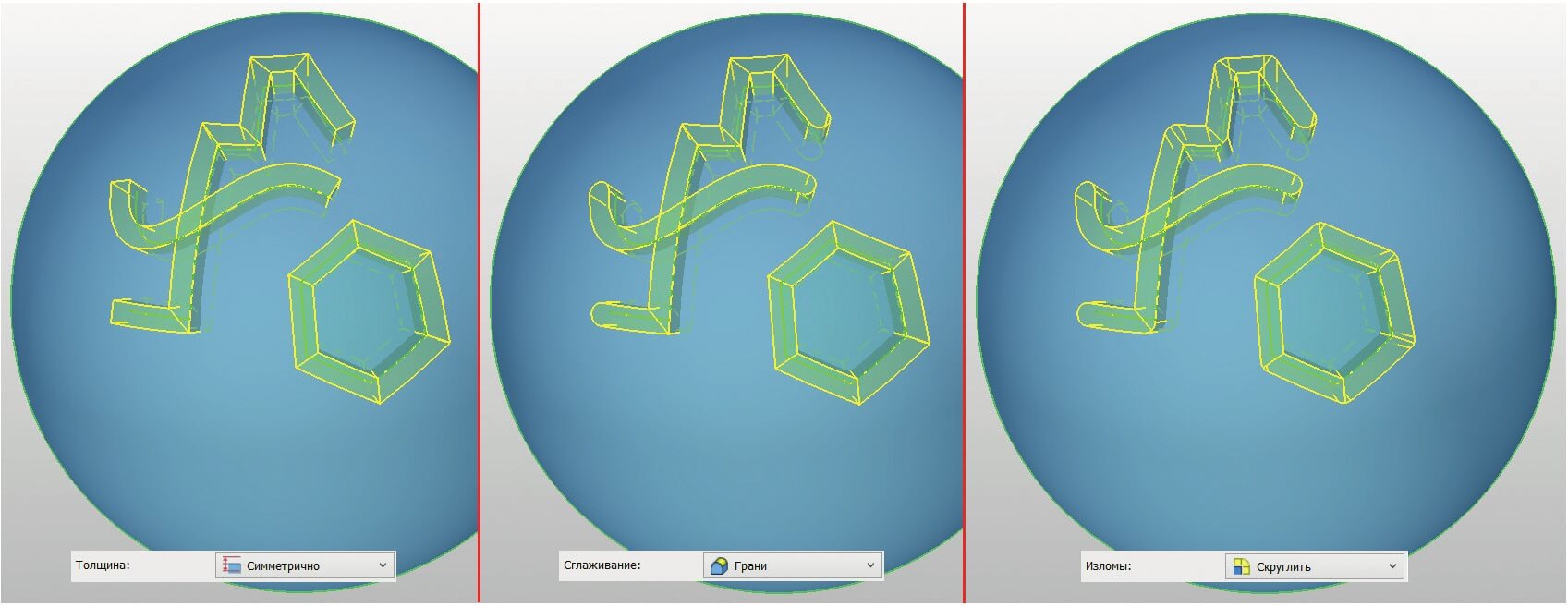
Рис. 13. Придание толщины, сглаживание торцов и изломов
В результате на исходном теле получаем пазы, имитирующие фрезерную обработку (рис. 14).
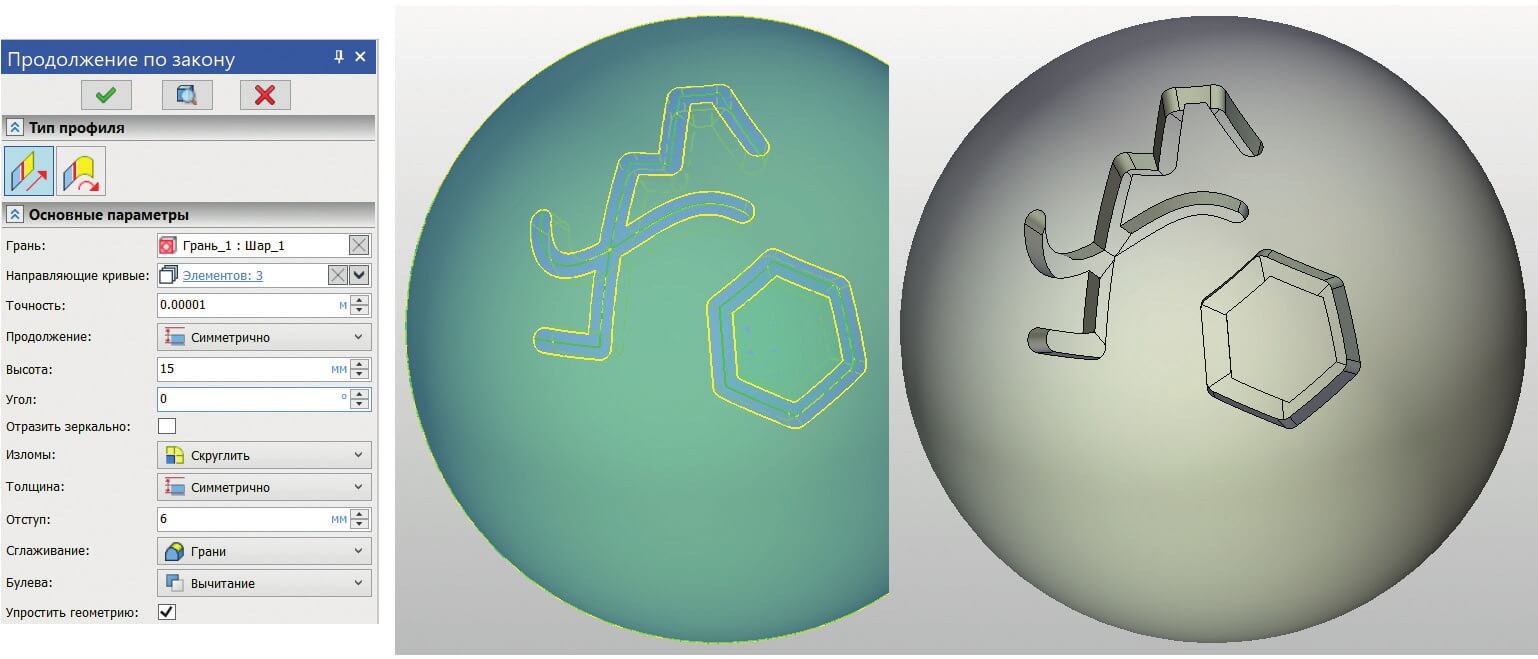
Рис. 14. Результат операции «Продолжение по закону»
Пересчёт данного примера на современном ПК занимает менее секунды. И всё же геометрические операции, задействованные в данном примере, являются довольно «дорогими» по используемым ресурсам (в силу универсальности операции). Тем не менее подобная операция является уникальной в своём роде.
Заключение
Как говорилось в начале статьи, подход поверхностного моделирования применяется во многих отраслях промышленности. Применяя базовые инструменты T-FLEX CAD, а также описанные выше операции, можно проектировать модели любой сложности, удовлетворяющие всем требованиям к форме изделия, его эргономичности и эстетичности.О других новых возможностях T-FLEX CAD 17 читайте в нашем материале «T-FLEX CAD 17 – новая отечественная САПР уже на пороге!»

