
По мнению экспертов компании LEDAS, эта статья представляет собой образцовый технологически-популярный материал, который изложен образцовым же русским языком.
Математическая модель физических тел
Начну издалека, а именно с математической модели объектов трёхмерного мира. Большинство ядер CAD-систем оперируют с граничным представлением. В переводе на человеческий язык это означает следующее: пространство делится на две части – заполненную материалом и всё остальное. Граница этих двух частей представляет собой стыкующиеся кусочки разных поверхностей так, чтобы между ними не было щелей. То, как именно стыкуются кусочки и какая часть заполнена материалом – называется «топологией». Но она не очень хорошо подходит для иллюстрации многопоточности. А вот описание поверхности… Штука, вроде, простая, пока не вступает в свои права вычислительная математика. Берётся (прошу прощения за столь вольный стиль изложения) декартова система координат, и в ней задаются функции радиус-вектора (x,y,z) в параметрической области (u,v). В формулах x, y, z, u, v – это числа с плавающей точкой. Для указания, какой кусочек поверхности брать, используются кривые. С ними уже разнообразнее: кривые могут быть определены как в области определения поверхности u(t), v(t), так и в трёхмерном пространстве (x,y,z). Здесь t – тоже число с плавающей точкой, называется «параметром кривой». Собственно, на кривых я и проиллюстрирую некоторые трудности, которые возникают, едва стоит заняться написанием кода.Перевод формул в числа
Итак, вычислительная математика: страна чудес, где, например, сумма меняется от перестановки слагаемых. Но это довольно тонкие эффекты, к которым порой приходишь через гораздо более насущные задачи. А именно – придумать способы подсчёта радиус-вектора (u,v) при произвольных допустимых значениях параметра t. Способов много: аналитические или специальные функции для каждой координаты, различные сплайны и так далее. Во всех способах есть ухищрения, которые позволяют уменьшить потребное число арифметических операций, и за каждый из этих способов приходится платить свою цену: или операций слишком много, или приходится заниматься поиском, или всё вместе. Причём, речь идёт именно об арифметических операциях, а не каких-то ещё, потому что большинство способов изобреталось в эпоху, когда в ходу были таблицы Брадиса, логарифмические линейки и механические арифмометры. Нужно ли говорить, что каждый знак после запятой нужно было обосновывать (о, да, неустойчивость алгоритмов!), потому как они переводились в человеко-часы? Нужно его обосновывать и теперь, потому что прогресс вычислительной техники позволил расширить круг решаемых задач, и ряд задач, которые некогда считались суперсложными, перешли в разряд даже не рутинных, а вспомогательных. Соответственно, требования к точности и быстродействию не стали менее актуальными. Точность недостаточна – результат будет практически неприменим. Точность избыточна – результат успеет устареть прежде, чем будет получен.Что такое кэширование и что оно даёт
Задача оптимизации вычислительного алгоритма формулируется так: сократить количество необходимых операций, поскольку оно определяет время вычислений. Для многих задач уже сформулированы эффективные вычислительные алгоритмы. Тем не менее, для прикладных задач наибольшую ценность представляют не те алгоритмы, которые входят в библиотеки, а реализованные самостоятельно, с учётом специфики применения.Практика показывает, что зачастую набор значений параметра, для которых вычисляется радиус-вектор, подчиняется некой закономерности или статистике. Именно на предположении о том, что значения параметра не являются произвольными, основан такой метод оптимизации, как кэширование данных.
Под кэшированием понимается сохранение неких промежуточных или конечных результатов, которые могут быть использованы повторно с целью сокращения объёма последующих вычислений. Область оперативной памяти, в которой хранятся те данные, которые предполагается использовать, называется кэшем; также под кэшем может пониматься сам набор данных.
Платой за использование этого способа оптимизации (кэширование) является дополнительный расход памяти, т.к. рассчитанные значения и параметры надо где-то хранить. Как показывает практика, явный учёт частных случаев встречается достаточно часто, чтобы быть реализованным для получения выигрыша во времени.
Следующий пример иллюстрирует, как работает кэширование.
Затраты на вычисление
Рассмотрим самое прекрасное, что есть в двумерии, согласно Пифагору – окружность. Всё просто: u(t) = cos(t), v(t) = sin(t) – единичный радиус, начало координат. Первым делом нужно «загнать» t в диапазон от 0 до 2π. Далее могут быть варианты, например, использовать формулы приведения (навешивать на синус и косинус знаки плюс и минус в зависимости от, скажем так, «обстоятельств»), а считать синус-косинус в диапазоне вчетверо более коротком – до π/2. Теоремой Пифагора пользоваться не будем, потому что там всё равно придётся расписывать ряд Тейлора, но уже для квадратного корня. Можно работать итерационным методом, кому что нравится.Перейдём к численным оценкам. Посчитаем, сколько потребуется выполнить арифметических операций, чтобы вычислить синус угла с заданной точностью, используя ряд Тэйлора. В качестве примера возьмём угол 30 градусов: для получения точного значения ½ до 15 знака (с машинной точностью) мне пришлось просуммировать 7 членов ряда:
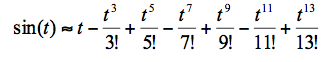
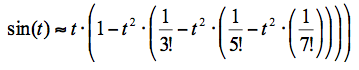
В том случае, когда нужно посчитать значения при двух близких значениях параметра, можно укоротить ряд Тейлора. Насколько близких и насколько укоротить – это зависит от требуемой точности. Допустим, нас устраивает точность до восьмого знака. Для вычисления значения косинуса с такой точностью потребует суммировать ряд до восьмой степени. Оценки показывают, что для разницы углов π/50 (как со знаком плюс, так и минус) ряд Тейлора для синуса и косинуса можно укоротить до третьей и четвёртой степеней, соответственно. А потом используются формулы для вычисления синуса и косинуса суммы углов:
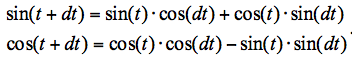
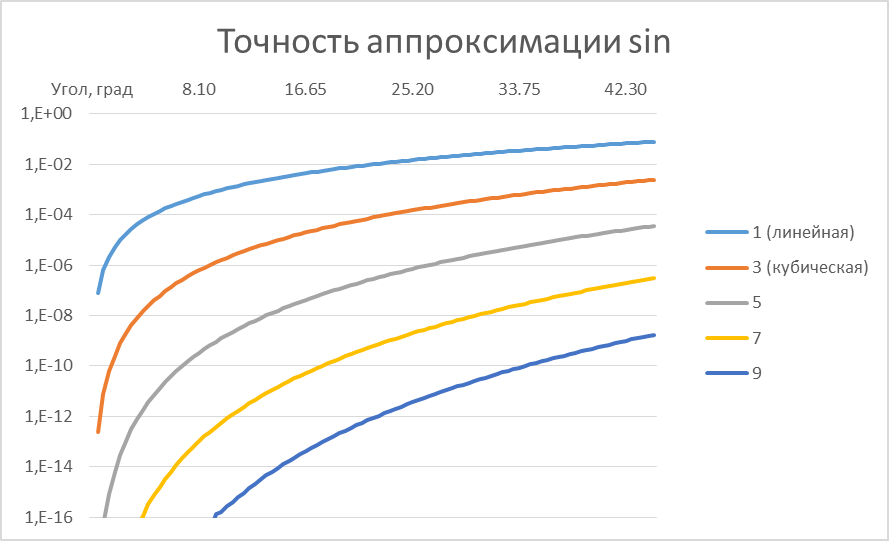
Рисунок 1. Точность аппроксимации функции многочленами разной степени
Понятно, что кэш сплайна будет отличаться от кэша дуги, что кэш поверхностей будет устроен иначе. Важен сам принцип.
Программная надстройка над аппаратным базисом
С тех пор, как многоядерные процессоры стали даже не просто доступны, а начали восприниматься как нечто само собой разумеющееся, всё более актуальной стала задача написания такого кода, который позволял бы задействовать аппаратные средства максимально эффективно. Ускорение может быть достигнуто за счёт одновременного выполнения разных расчётов на разных процессорах или ядрах.Само по себе наличие нескольких ядер не обеспечивает ускорения вычислений, а лишь предоставляет для этого аппаратную возможность. Многопоточность – это всего лишь один из способов задействовать имеющиеся аппаратные возможности. Потоки – это объекты ядра операционной системы, которые могут очень эффективно взаимодействовать между собой, используя, грубо говоря, оперативную память. В идеале для корректной работы потоков нужно, чтобы они не использовали одни и те же участки памяти. В случае геометрического ядра – одни и те же кэши. К сожалению, в случае граничного представления геометрическая модель так устроена, что для подавляющего большинства операций не гарантирует такого разделения, если всё оставить в таком виде, как было в эпоху одноядерных процессоров.
Оптимизируя алгоритмы для многопоточной среды, не следует полагаться на ускорение, которое бы достигалось только за счёт использования многоядерности. Во-первых, потому что не все задачи хорошо распараллеливаются. Во-вторых, следует учитывать, что потоками и аппаратными ресурсами, например, ядрами, управляет не прикладная программа и не геометрическое ядро, а операционная система. Сам тот факт, что работа программы зависит не только от труда её автора, указывает на необходимость оптимизации того кода, который исполняется внутри потока. В некотором смысле давно разработанные и оптимизированные «однопоточные» алгоритмы являются эталоном быстродействия для своих «многопоточных» модификаций.
Пока не встал вопрос о многопоточности, пожалуй, единственным фактором, который ограничивал использование кэшей, был объём доступной оперативной памяти. Требование работы в многопоточной среде привело к ревизии архитектуры программных комплексов и практической реализации вычислительных алгоритмов.
Собственно, обеспечение работоспособности в многопоточной среде при сохранении эффективности «однопоточной» реализации и является одним из ноу-хау C3D Labs. При развитии в этом направлении приходится модифицировать архитектуру системы так, чтобы выполнялся ряд условий:
- Обеспечивалась максимальная эффективность от использования многопоточности.
- Сохранялась эффективность в однопоточном варианте.
- Обеспечивалась максимальная совместимость кода.
- Условия 1-3 распространялись на максимально возможное число операций.
Есть и другие условия, например, требование кроссплатформенности. Оно накладывает ограничение на используемые технические средства. Применение технологии OpenMP для оптимизации кода ядра C3D как раз позволило одновременно решить проблемы кроссплатформенности и совместимости.
Первым практическим результатам этой работы и был посвящен доклад моего коллеги Алексея Горячих на конференции Intel, о которой читатели уже знают.

