

Эта заметка запускает цикл статей, посвященных новому типу кривых и поверхностей, разработанному в компании C3D Labs в качестве нового функционала поверхностного моделирования для геометрического ядра C3D Modeler.
Первая часть из данного цикла освещает основные моменты, необходимые для понимания читателем главных преимуществ рассматриваемого класса кривых и его назначения в инженерной геометрии.
Вторая часть посвящена реализации методов F-кривых в C3D Modeler.
В третьей части будут приведены примеры практического применения C3D FairCurveModeler при моделировании различных изделий.
Оригинал статьи в блоге C3D Labs
В современном мире повсеместно востребованы CAD-системы, позволяющие моделировать сложные кривые и поверхности. Эти возможности задействованы при решении многих проектных задач в самых разных областях науки и техники. Однако даже если CAD-система поддерживает моделирование кривых и поверхностей класса А, она не обеспечивает надлежащего качества так называемых функциональных кривых по критериям плавности.
Перед разработчиками C3D Labs встала задача реализации такого функционала, который позволил бы моделировать кривые линии и, соответственно, поверхности самого высокого качества. В результате проведенных изысканий в области геометрического моделирования на свет появился C3D FairCurveModeler — новый раздел геометрического ядра C3D Modeler, позволяющий строить кривые класса F.
В данной статье анализируются требования к функциональным кривым, дается описание их преимуществ перед другими кривыми, а также приводятся примеры практического применения функционала C3D FairCurveModeler.
Введение в понятие функциональных кривых
Что такое функциональные кривые
К новому типу кривых относятся плоские и пространственные кривые, которые обеспечивают некоторую функциональную характеристику объекта, в связи с чем их целесообразно называть функциональными кривыми [1].
Область применения таких кривых весьма широка и распространяется в основном на проектные задачи, возникающие в разных отраслях техники. Например,
- задача по максимизации подъемной силы при минимизации лобового сопротивления при моделировании профиля крыла самолета (рис. 1.1);
- задача поиска максимальной плавности трассы при заданных ограничениях для обеспечения комфортной и безопасной езды на транспортном средстве.
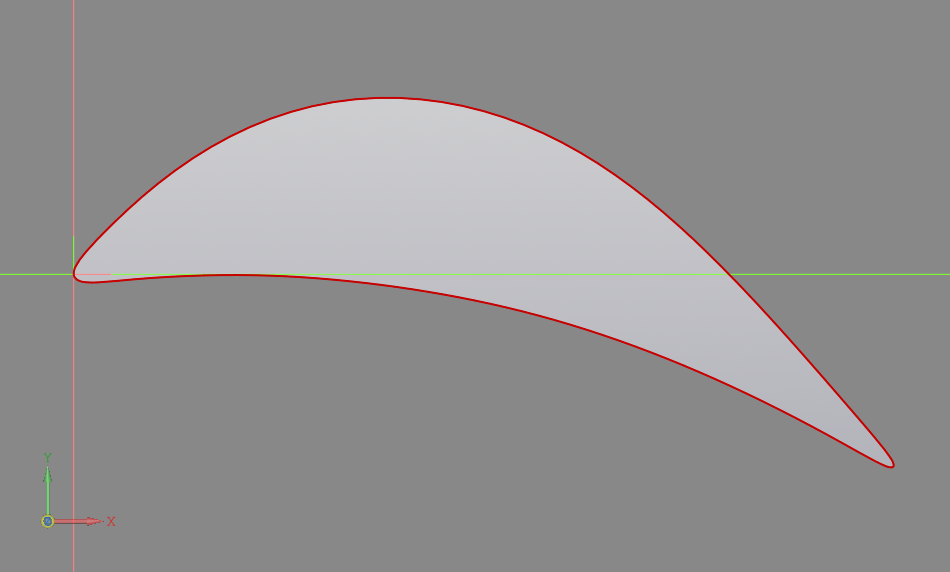
Рис. 1.1. Профиль крыла
Среди функциональных кривых можно выделить подкласс инженерных аналитических кривых, которые единственным оптимальным образом обеспечивают некоторую проектную характеристику объекта. К таким кривым, например, можно отнести спираль Архимеда, используемую для построения профиля зубьев зубчатого колеса, а также брахистохрону — кривую наискорейшего спуска для транспортировки предметов.
В остальных случаях функциональные кривые имеют свободную форму. Такие кривые могут быть локально-выпуклыми (с постоянным знаком функции кривизны) и иметь точки перегиба (участки с разным знаком функции кривизны).
Кроме того, функциональные кривые могут быть пространственными и, соответственно, иметь кручение.
Рассмотрим подробнее, что представляют собой функциональные кривые и чем они отличаются от обычных гладких кривых.
Требования качества к функциональным кривым
К параметрам плавности рассматриваемых инженерных кривых предъявляются повышенные требования, которые являются универсальными для данного типа кривых и не зависят от специфики проектируемых объектов. Ниже приводится список данных требований с пояснениями:
а) высокий, не ниже 4-го, порядок гладкости
Гладкость — это свойство функции или геометрической фигуры (кривой, поверхности и др.), определяющее, дифференцируема ли функция на всём множестве определения или имеется ли у каждой точки данной фигуры окрестность, допускающая задание с помощью дифференцируемых функций.
В различных видах проектирования используются сплайны разного порядка гладкости. Например,
- при моделировании трасс дорог используются клотоидные сплайны, а гладкость обеспечивается не ниже 2-го порядка;
- для профилирования кулачка распределительного вала высокоскоростных двигателей необходима гладкость не ниже 3-го порядка, поэтому проектирование профиля начинается с вычерчивания плавного графика 3-й производной [2];
- при моделировании пространственных кривых для обеспечения непрерывности функции кручения кривая должна иметь 3-й порядок гладкости;
- из анализа пространственной криволинейной траектории движения материальной точки следует, что пространственная кривая с плавным кручением должна иметь 4-й порядок гладкости [3].
б) отсутствие или минимальное число экстремумов кривизны
Плавность кривой также зависит от формы графика изменения кривизны вдоль линии движения.
Возвратимся к примеру с материальной точкой. Поскольку осцилляция функции кривизны согласно основному уравнению динамики [3] вызовет пульсацию центробежных сил, действующих на материальную точку, участок линии движения должен иметь минимальное число экстремумов кривизны или минимальное число вершин кривой.
Наличие лишних экстремумов кривизны, например, у формы технических изделий и объектов дизайна, может вызвать следующие негативные явления:
- неоправданное биение толкателя кулачкового механизма, следствием которого является преждевременный износ механизма;
- залипание почвы на участке плуга с концентрацией кривизны у траектории движения почвы, что приводит к увеличению сопротивления плуга и, следовательно, повышению энергоемкости процесса вспашки (рис. 1.2) [4];
- при лишних экстремумах кривизны на аэродинамическом профиле — неоправданная пульсация среды, обтекающей профиль, что увеличивает его лобовое сопротивление и может спровоцировать срыв потока;
- необходимость лишних торможений и разгонов, что увеличивает энергозатраты на перемещение по трассе транспортного средства [5];
- эффект кривых зеркал у кривых кузовных поверхностей и архитектурных форм [6];
- неправильное визуальное восприятие объектов компьютерной графики и CAD [7].
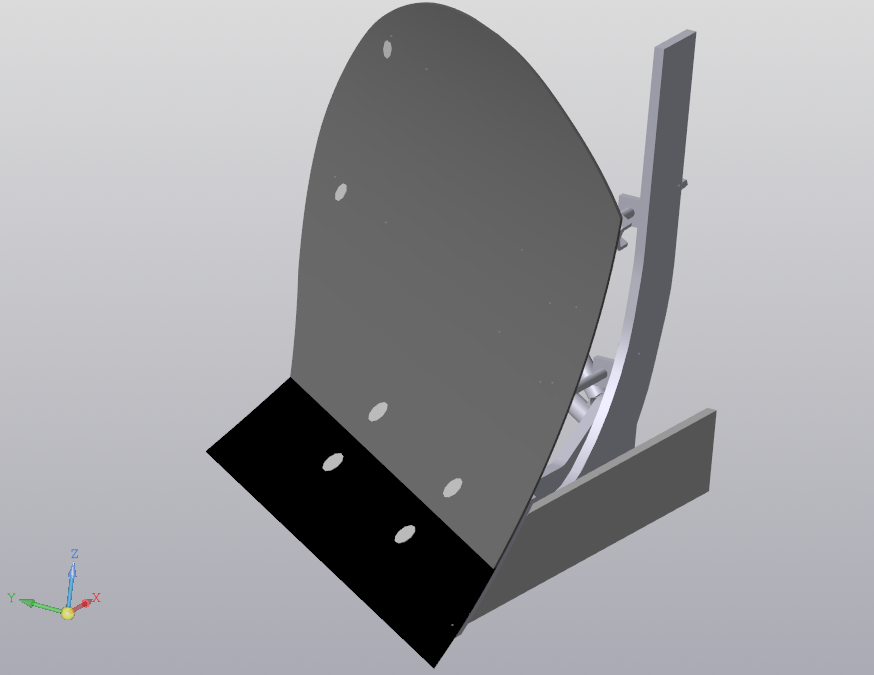
Рис. 1.2. Сборка плуга в КОМПАС-3D
в) малые значения вариации кривизны и скорости ее изменения
В некоторых прикладных областях вводится требование минимизации вариации кривизны, следовательно, концентрация кривизны должна быть ограничена по максимальному значению.
Например, такое ограничение минимального значения радиуса кривизны (максимальной кривизны) естественным образом вводится при проектировании дорог: минимальный радиус виража ограничивается из расчета допустимой скорости транспортного средства [8, 9].
Важным параметром качества кривой является скорость изменения кривизны. При проектировании трассы дороги этот параметр регламентирует скорость нарастания центробежной силы, действующей на автомобиль на виражах, и легко контролируется благодаря применению сегментов клотоиды с линейным изменением функции кривизны [8, 9].
г) малое значение потенциальной энергии кривой
Считается, что плавность кривой напрямую связана с ее потенциальной энергией. Необходимость выбора функциональной кривой с малым значением потенциальной энергии основывается на предположении, что при движении объекта с функциональной поверхностью с большой скоростью среда, обтекающая объект, ведет себя как упругое тело. Очевидно, что для деформации упругой среды по линиям тока с меньшей потенциальной энергией будет затрачиваться меньшая работа. При движении материальной точки по вогнутой криволинейной траектории с учетом трения работа, затрачиваемая на перемещение, будет меньше при меньшем значении потенциальной энергии траектории перемещения [1].
Кривая, имеющая минимальное значение потенциальной энергии, называется эластикой [10]:
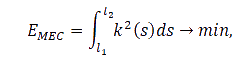
где EMEC — потенциальная энергия кривой;
k(s) — ее кривизна;
l2 и l1 — начало и конец интервала.
Эластика может быть представлена в виде осевой линии деформированной упругой рейки между двумя грузиками (ducks). Качество эластик апробировано многовековым опытом судостроения. Гибкие рейки (физические сплайны) применялись для вычерчивания профилей шпангоутов, батоксов и ватерлиний при проектировании и строительстве судов, а позднее автомобилей и самолетов.
д) эстетический анализ кривых
Помимо предложенных выше объективных критериев плавности качество кривой необходимо оценивать также и с позиций законов технической эстетики. Существует такой подход к оценке эстетичности кривой, когда форма кривой базируется на математических характеристиках форм, выявленных у объектов реального мира (например, очертания крыльев бабочек) [11, 12].
Для моделирования красивых (эстетических) форм предлагаются так называемые log-эстетические кривые, имеющие линейный график кривизны в логарифмической шкале [13 - 15]. Множество известных спиралей, в том числе клотоида, являются частными случаями кривых этого класса. В работе [16] был предложен наиболее обобщенный класс кривых с монотонной функцией кривизны, называемый суперспиралями. Уравнения этих кривых выражаются через Гауссовы гипергеометрические функции и численно интегрируются адаптивными методами типа метода Гаусса — Кронрода.
Однако множество эстетических кривых не ограничивается только множеством log-эстетических кривых. Кривые могут иметь произвольно сложные плоские и пространственные формы и быть вполне эстетичными.
Авторы работы считают, что приоритетной является оценка по критериям плавности. Экспертная оценка с позиций законов технической эстетики (лаконичность, целостность, выразительность, пропорциональная согласованность, композиционное равновесие, структурная организованность, образность, рациональность, динамичность, масштабность, пластичность, гармоничность) правомерна только после оценки на плавность.
Весьма показательна в этом смысле работа [17], в которой приводятся графики экспертной оценки эстетического качества кривых с различными параметрами плавности (рис. 1.3). Наиболее высокая экспертная оценка у кривых, которые отвечают базовым требованиям к функциональным кривым (одновременно малое значение кривизны и малая скорость изменения кривизны).
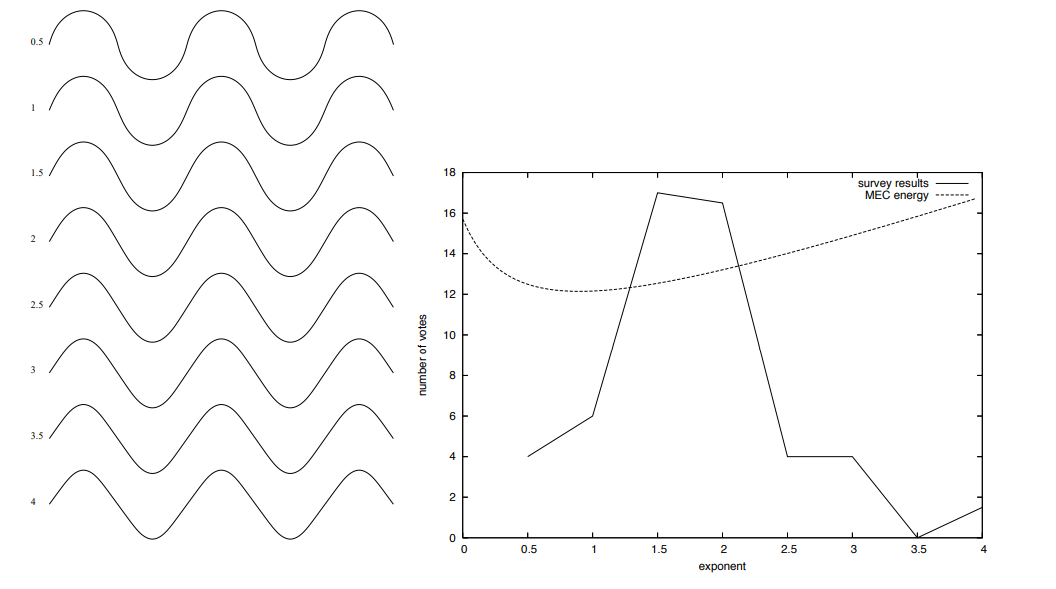
Рис. 1.3. Тест из работы Levien'а (2009)
Промежуточные итоги
С учетом всех вышеупомянутых требований для построения очень плавной траектории движения необходимы:
- минимальное число опорных точек моделируемой сплайн-траектории движения и высокий, не ниже 4-го, порядок гладкости;
- плавное кручение пространственной кривой;
- ограничение максимального значения кривизны и скорости ее изменения;
- минимизация функционала потенциальной энергии.
Функциональные кривые, параметры которых соответствуют приведенным требованиям, называются кривыми класса F [1].
Здесь важно отметить для сравнения, что именно эти жесткие требования к параметрам плавности и отличают кривые данного класса от кривых класса A. Последние являются формообразующими поверхностей класса А — высококачественных по критериям эстетики поверхностей внешних кузовных поверхностей. “Хорошая” кривая для этих поверхностей будет иметь график кривизны с небольшим числом участков монотонного изменения кривизны [18]. Данное требование можно сравнить с требованием минимальности количества экстремумов кривизны у функциональных кривых.
Таким образом, кривые класса А представляют кривые для формообразования поверхностей в промышленном дизайне (рис. 1.4), в то время как функциональные кривые являются инженерными кривыми. Такие кривые высокого качества также принято называть плавными кривыми (от faired curves, fairing curves). Здесь важно не путать последние с гладкими кривыми, которые являются кривыми самого низкого качества — первого порядка гладкости [19].

Рис. 1.4. Модель снегохода
Библиографический список
- Муфтеев В.Г., Мударисов С.Г., Фархутдинов И.М. и др. Обоснование выбора оптимальной формы функциональной кривой динамической поверхности технического изделия // Известия международной академии аграрного образования, 2013. Вып. 17. С. 90-93.
- Рожков А.П. Кулачок привода клапана. Авторское свидетельство №1237778, приоритет от 5 сентября 1983 г., зарегистрирован 15 февраля 1986, с 1 июля 1991 выдан патент взамен авторского свидетельства.
- Карякин Н. И., Быстров К. Н., Киреев П. С. Краткий справочник по физике. - М.: Высшая школа, 1969. - 600 с.
- Муфтеев В. Г., Мударисов С. Г., Марданов А.Р. Моделирование рабочей поверхности плуга // Материалы Всероссийской научно-практической конференции, посвященной 75-летию со дня открытия Чувашской государственной сельскохозяйственной академии. - Чебоксары: Изд-во ЧГСА, 2006. С. 479-482.
- Абдуллин М. М., Фаттахов М. М., Федоров П. А. Архитектурно-ландшафтное проектирование дорог с учетом дорожной геометрии: Учебник. - Уфа: Нефтегазовое дело, 2011. - 320 с.
- Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве: Пер. с англ. - М.: Мир, 1982. - 304 с., ил.
- Ziatdinov R. Visual Perception, Quantity of Information Function and the Concept of the Quantity of Information Continuous Splines // Scientific Visualization. 2016. No 8. Vol. 1. P. 168-178.
- В. Ф. Андреев О. В., Бабков В. Ф. Справочник инженера-дорожника. 2-е изд., перераб. и доп. - М.: Транспорт, 1969. - 552 с.
- Справочная энциклопедия дорожника / Минтранс России, Росавтодор. Т. 5. Проектирование автомобильных дорог // Под ред. Г. А. Федотова, П. И. Поспелова. - М.: Информавтодор, 2007. - 815 с.
- Shen, J., Kang, S. H., Chan, T. F. Euler's elastica and curvature-based inpainting // SIAM Journal on Applied Mathematics. 2003. No 63. Vol. 2. P. 564-592.
- Kineri, Y., Endo, S., Maekawa, T. Surface design based on direct curvature editing // Computer-Aided Design. 2014. Vol. 55. P. 1-12.
- Harada, T. Study of quantitative analysis of the characteristics of a curve // Forma. 1997. Vol. 12. No. 1. P. 55-63.
- Yoshida, N., Saito, T. Interactive aesthetic curve segments // The Visual Computer. 2006. No. 9. Vol. 22. P. 896-905.
- Gobithaasan, R.U., Miura, К. T. Aesthetic Spiral for Design // Sains Malaysiana. 2011. Vol. 40. No. 11. P. 1301—1305.
- Inoguchi, J. Attractive plane curves in differential geometry. In Mathematical Progress in Expressive Image Synthesis, 3rd ed. // Mathematics for Industry. Springer: Singapore, 2016. Vol. 24. P. 121-135.
- Ziatdinov, R. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function// Computer Aided Geometric Design. 2012. Vol. 29. No.7. P. 510-518.
- Levien, R. L. From Spiral to Spline: Optimal Techniques in Interactive Curve Design. PhD.thesis, University of California, Berkeley, 2009.
- Farin, G. Class A Bézier curves // Computer Aided Geometric Design. 2006. No. 23.
- Погорелов А.В. Геометрия. – М.: Наука, 1983. - 288 с.

