

Продолжение цикла статей, посвященных новому типу кривых и поверхностей, разработанному в компании C3D Labs в качестве нового функционала поверхностного моделирования для геометрического ядра C3D Modeler.
В этой части описывается реализация методов F-кривых в C3D Modeler.
В первой части были освещены основные моменты, необходимые для понимания читателем главных преимуществ рассматриваемого класса кривых и его назначения в инженерной геометрии.
В третьей части будут приведены примеры практического применения C3D FairCurveModeler при моделировании различных изделий.
Реализация методов F-кривых в C3D Modeler
Что такое C3D FairCurveModeler
C3D FairCurveModeler — это библиотека моделирования плавных кривых, реализованная как совершенно новый раздел геометрического ядра C3D Modeler, расширяющий его возможности для поверхностного моделирования.
Кривые класса F, описанные в прошлом блоке статьи, моделируются с помощью методов C3D FairCurveModeler. Помимо возможности построения кривых высокого качества по критериям плавности методы также удовлетворяют следующим требованиям:
- устойчивость формообразования, или изогеометричность;
- инвариантность относительно аффинных и проективных преобразований;
- гибкость;
- инструментальное разнообразие;
- возможность изогеометрической аппроксимации аналитических кривых с сохранением их базовых свойств.
Функционал C3D FairCurveModeler описывается с помощью терминов инженерной геометрии. Модель кривой в инженерной геометрии называется определителем [20] и состоит из геометрической части и алгоритма генерации точек кривой или процедуры построения аппроксимирующего сплайна. Геометрическую часть определителя можно рассматривать как геометрический определитель кривой. Наиболее привычными и естественными видами геометрического определителя являются множества точек (вида опорной ломаной) или множества касательных прямых (в частности, вида касательной ломаной). Кроме того, в инженерной геометрии используются так называемые управляющие сплайновые полигоны NURBS кривых.
Различные виды геометрических определителей имеют свои достоинства и недостатки. Ломаная инцидентности позволяет точно позиционировать кривую, касательная ломаная однозначно и точно задает форму моделируемой кривой, S-полигон NURBS кривой высокой степени позволяет локально изменять форму кривой и гарантирует высокое качество пространственных кривых по критериям плавности кривизны и кручения.
В библиотеке C3D FairCurveModeler используется также уникальный геометрический определитель — геометрический определитель Эрмита (ГО Эрмита) второго порядка фиксации. ГО Эрмита представляет собой опорную ломаную, оснащенную в каждой своей вершине касательным вектором и вектором кривизны.
Фундаментальные основы C3D FairCurveModeler
Ниже приводятся четыре фундаментальных «открытия», ставшие отправной точкой в разработке функционала моделирования плавных кривых.
1. Теоретическим фундаментом или первым «краеугольным камнем» C3D FairCurveModeler является теория параметризации, или теория исчисления параметров. На ее основе было обобщено понятие сплайна как множества базовых кривых, имеющих совпадающие геометрические параметры в произвольных точках опорной ломаной. В традиционных сплайнах базовые кривые имеют совпадающие параметры только в точках стыка сегментов сплайна.
Первым открытием является метод определения базиса сплайна как множества конических кривых двойного соприкосновения на локально-выпуклой опорной ломаной (рис. 2.1).
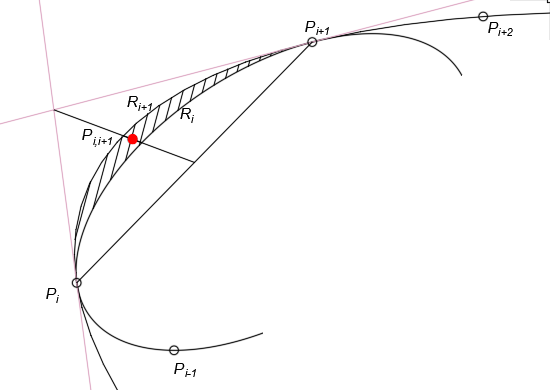
Рис. 2.1. Конические кривые двойного соприкосновения
Смежные кривые образуют на общем сегменте ломаной “линзу”. Напряженность сплайна характеризуется величиной отклонения смежных аналитических кривых базиса сплайна и визуально легко оценивается по величине линзы между смежными кривыми.
2. Вторым “краеугольным камнем” фундамента является алгоритм генерации точек виртуальной кривой (V-кривой) на базисе сплайна дискретного множества конических кривых двойного соприкосновения. Метод V-кривой разработан в C3D Labs в рамках приведенного выше подхода.
Точки кривой генерируются в области линз, что уменьшает напряженность сплайна, построенного на сгенерированных точках. Затем на множестве сгенерированных точек вновь определяется множество конических кривых двойного соприкосновения. Последовательность этих операций в пределе определяет виртуальную кривую класса C5 [21].
Виртуальная кривая (V-кривая) обладает рядом замечательных свойств:
- минимальным числом экстремумов кривизны;
- дуальностью (как и коническую кривую, V-кривую можно определять не только на опорных точках, но и на касательных);
- аффинной инвариантностью;
- малой чувствительностью к распределению точек на контуре кривой.
Важным следствием этих свойств является возможность геометрически точного моделирования конических кривых.
3. Третий «краеугольный камень» — изогеометрическая аппроксимация виртуальной кривой посредством рациональной сплайновой кривой Безье (NURBzS кривой) — один из геометрически ориентированных методов изогеометрического построения NURBS кривой.
Графоаналитический алгоритм состоит из следующих простых операций:
а) Конические кривые двойного соприкосновения на общем сегменте опорной ломаной рассматриваются как кривые Безье 2-й степени с B-полигонами в виде 2-звенников (рис. 2.2);
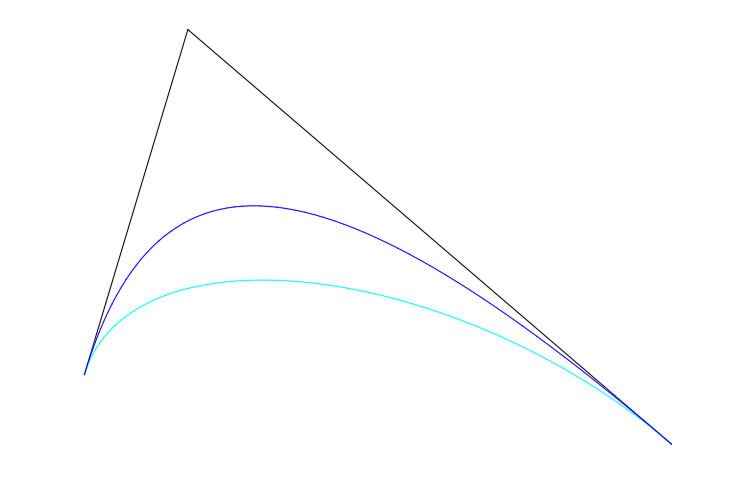
Рис. 2.2. Конические кривые двойного соприкосновения
б) У кривых Безье повышается степень до 3-й с (рис. 2.3) с B-полигонами в виде 3-звенников;

Рис. 2.3. Преобразование конических кривых до рациональных кривых Безье 3-й степени
в) Результирующий B-полигон получается усреднением исходных B-полигонов. Среднее звено результирующего B-полигона параллельно исходным и лежит на равном расстоянии от них (рис. 2.4).
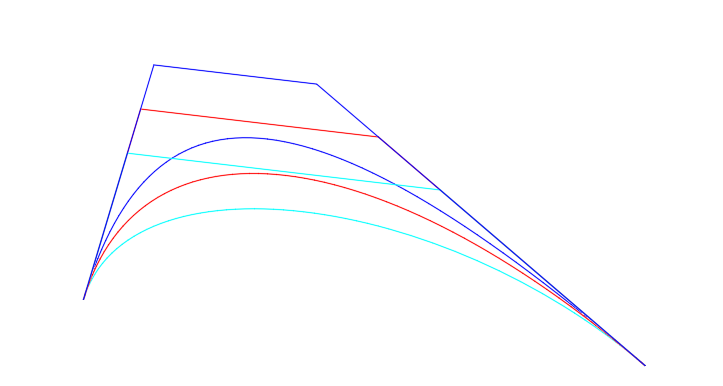
Рис. 2.4. Построение результирующего B-полигона
Поскольку усредненный B-полигон будет также выпуклым, как и исходные B-полигоны, то обеспечивается строгая изогеометричность.
г) Уточняются значения кривизны в концевых точках результирующей кривой по значениям исходных кривых.
Алгоритм имеет модификацию. При резких изменениях кривизны, когда одно значение близко к нулевому, B-полигон корректируется таким образом, что кривая Безье, определенная на скорректированном B-полигоне, имеет точную меньшую кривизну.
4. Четвертый «краеугольный камень» — изогеометрическая аппроксимация виртуальной кривой посредством B-сплайновой кривой.
Ключевым моментом здесь является отказ от традиционного подхода, при котором считается, что опорные точки должны совпадать с узловыми точками сплайна. Сплайн должен проходить через точки опорной ломаной, но узлы сплайна (или любые точки сплайна с фиксированными значениями внутреннего параметра) не совпадают с вершинами опорной ломаной.
Алгоритм является эвристическим — аналогом ручного редактирования S-полигона. Для построения используются исходные касательные прямые в точках V-кривой. Пересечения касательных прямых определяют вершины S-полигона (рис. 2.5).
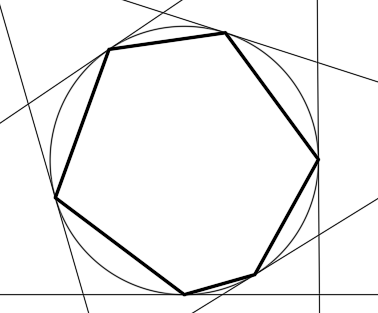
Рис. 2.5. ГО Эрмита первого порядка фиксации
На S-полигоне в текущей итерации вычисляются расстояния от точек до сплайна. Касательная прямая параллельно себе перемещается на величину невязки δij в сторону уменьшения невязки (рис. 2.6).
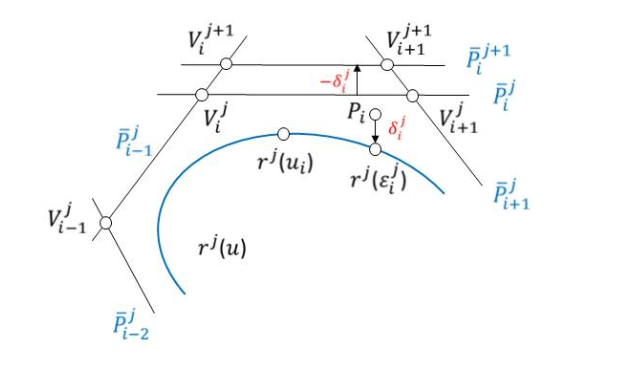
Рис. 2.6. Итерация приближения сплайна
Затем итерация повторяется. Приведенный алгоритм изогеометрической аппроксимации является типичной эвристической графоаналитической процедурой.
Методы построения кривых C3D FairCurveModeler
Далее приводится описание алгоритмов работы методов C3D FairCurveModeler для моделирования кривых высокого качества различной формы.
Моделирование кривых сложной формы
Исходный ГО кривой сложной формы структурируется, определяются точки перегиба. По точкам перегиба исходный ГО разбивается на ряд локально-выпуклых участков. На каждом локально-выпуклом участке строится виртуальная кривая (V-кривая). При определении V-кривой на участке ломаной с концевой точкой, принадлежащей точке перегиба, задается нулевое значение кривизны в концевой точке.
Моделирование кривых пространственной формы
Исходная пространственная ломаная развертывается на плоскости таким образом, что сохраняются длины звеньев и углы между звеньями. Затем ломаная структурируется и определяется V-кривая.
Для сглаживания прерывистого кручения пространственной NURBzS кривой выполняется следующая процедура, привязанная к команде повышения степени.
Степень кубической NURBzS кривой повышается до шестой. Сегмент NURBzS кривой имеет B-полигон с 7 вершинами. У смежных сегментов определяются соприкасающиеся плоскости в концевых точках. Эти плоскости определяются тремя концевыми точками B-полигонов. У смежных сегментов определяется биссекторная плоскость к двум смежным соприкасающимся плоскостям. Третьи вершины B-полигонов, считая от общей точки, проецируются на биссекторную плоскость.
Моделирование B-сплайновой поверхности высоких степеней
В функционал C3D FairCurveModeler нет необходимости добавления методов для построения и редактирования B-сплайновых поверхностей, так как для этого используются только методы построения B-сплайновых кривых.
Каркасно-кинематическое представление B-сплайновой поверхности, принятое в инженерной геометрии, позволяет разбить процесс построения поверхности на два этапа.
- Первый этап — построение образующих B-сплайновых кривых с применением V-кривых (рис. 2.7, 2.8);
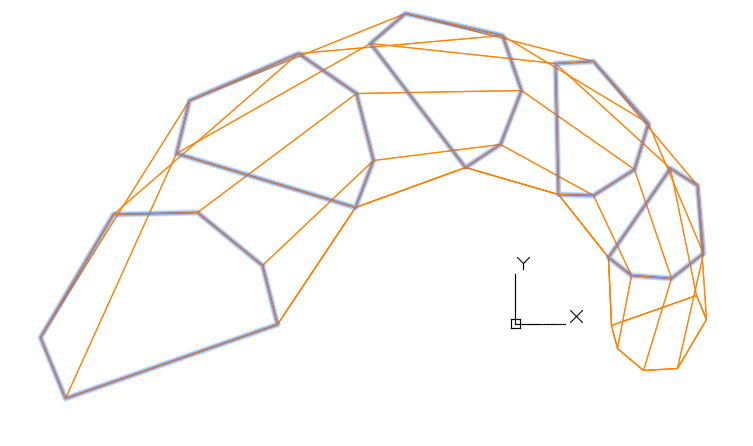
Рис. 2.7. Исходная сеть опорных точек
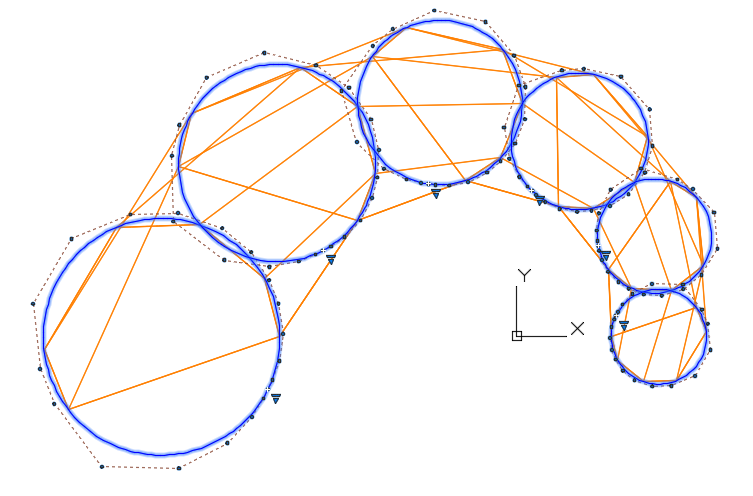
Рис. 2.8. Каркас S-полигонов образующих B-кривых
- Второй этап — построение направляющих B-сплайновых кривых с применением V-кривых (рис. 2.9, 2.10).
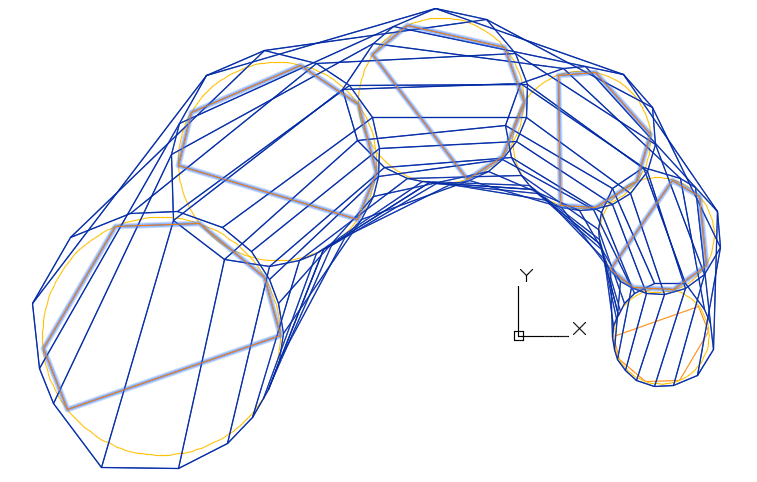
Рис. 2.9. Сеть S-полигонов образующих B-кривых
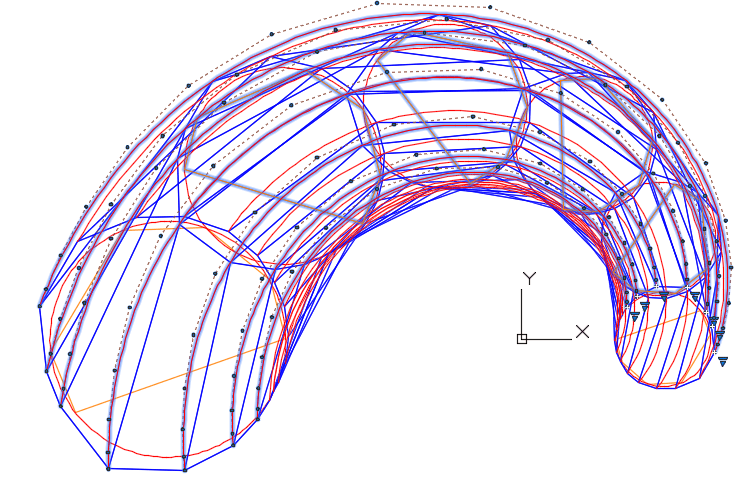
Рис. 2.10. Каркас S-полигонов формирует S-фрей B-сплайновой поверхности
Библиографический список
В списке литературы используется сквозная нумерация по трем частям, см. начало.
20. Муфтеев В. Г. Конструирование криволинейных поверхностей на основе метода огибающей и параметрических В-сплайнов: Дис. ... канд. техн. наук. Киев, 1986. 274 с.
21. Муфтеев В.Г. Конструирование плоских кривых методом огибающей // Изв. ВУЗов. Авиационная техника. 1980. № 4. С. 43-47.

