Мы продолжаем серию интервью
«История одного ядра» с командой C3D Labs о том, как создается российское геометрическое ядро. Сегодня свою историю рассказывает Александр Максименко, руководитель разработки решателя геометрических ограничений
C3D Solver.
Александр Максименко:
- Мог стать офицером-ракетчиком, но выбрал программирование
- В 16 лет самостоятельно выучил Basic, Assembler и Fortran
- Участвовал в разработке трех геометрических решателей — двумерного и трехмерного в C3D Solver и параметрического решателя в КОМПАС-3D
- Младший брат тимлида команды визуализации Эдуарда Максименко
Благодаря
интервью с Эдуардом мы знаем, что в детстве ты жил на Камчатке в военном гарнизоне. Каким запомнилось это место?
Я прожил на Камчатке до 13 лет, и воспоминания остались самые хорошие и радостные — притягательная природа, море. Летом по утрам бегали на отлив собирать рыб и моллюсков. Иногда я притаскивал домой рыбок и держал их в 5-литровых банках. Лазили по сопкам, собирали кедрач и рябину — она там другая, крупная, кисло-сладкая. На рыбалку часто ходили. Для ребенка это очень интересный край.
Потом вы вернулись на большую землю…
В 1989 году отец уволился в запас, мы переехали в Крым, а потом в Коломну. Так я сменил три школы: после гарнизонной год проучился в Балаклаве, а заканчивал уже в Коломне.
После школы ты поступил в университет в Коломне?
Нет, сначала была история с военным училищем. В военкомате я увидел объявление, что Санкт-Петербургское высшее зенитное ракетное командное училище предлагает получить сразу две специальности — военную и гражданскую «Радиоинженер». Меня это заинтересовало, и я уехал учиться, а через год подал рапорт на отчисление. Срочную службу дослужил в войсках и поступил в Коломенский институт МГОУ, сразу на второй курс.
Военное дело оказалось не твоим?
В училище все складывалось нормально, и у меня могла бы получиться военная карьера, но программирование перетянуло.
Расскажи, с чего все началось? Как ты стал тем, кого сегодня называют «гиками»?
Влияние шло от отца. Он хоть и военный, офицер ВМФ, но его настоящим увлечением была электроника. Он дал мне основы, как будто предчувствуя, что наступает цифровая эпоха. Например, двоичную систему счисления я знал еще в средних классах, знал, как в микросхемах кодируются сигналы. На самом деле ничего сложного для семиклассника в этом нет.
Твой первый язык программирования?
Basic, потом Assembler, Fortran.
Первый компьютер?
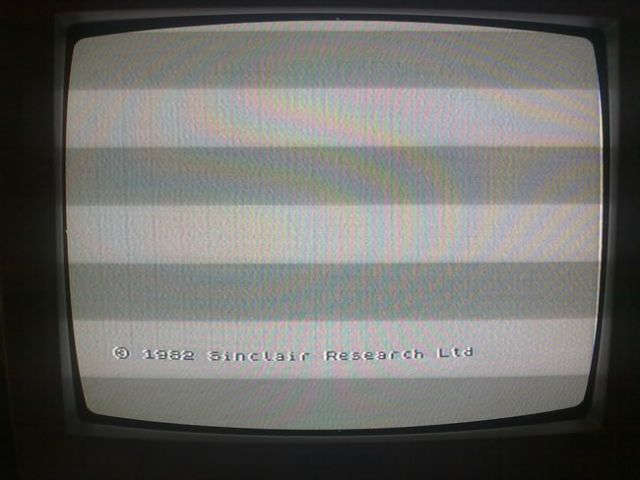
ZX Spectrum — мы его собрали сами. Эдик ездил за деталями на Митинский радиорынок — он тогда уже вернулся из армии и работал, а я учился в школе. Мы вдвоем паяли компьютер, но главная сложность заключалась в его настройке. Если просто спаять, то он сразу не заработает. Где-то мог быть дефект на дорожке — надо было зачистить, прощупать осциллографом все сигналы. Когда нам первый раз удалось его запустить, то на черно-белом экране телевизора «Горизонт» мы увидели текст «Sinclair Research Ltd 1982». Это означало, что запустилась операционка со встроенным Basic. Компьютер выдавал аналоговый видеосигнал, и мы подстыковали его к телевизору.
Правда, потом возникла досадная неприятность: провод питания упал на плату и сгорели самые чувствительные микросхемы памяти. Мы их заменили, оформили корпус с клавиатурой, и дальше началось мое знакомство с программированием. Это был примерно 1993 год, я учился в 10 классе.
На том же компьютере я выучил Assembler, пробовал писать короткие экспериментальные программки, например примитивный диктофон с двухуровневым квантованием сигнала. Он потом воспроизводил жуткий хрип, как у заболевшего фарингитом. ZX-Spectrum до сих пор лежит в гараже — оставил его на память.
Еще одна машина, которую мы собрали — Орион-128, советский радиолюбительский компьютер. Он интересен тем, что его можно было расширять, добавлять к нему устройства. Однажды подсоединили к нему 5-дюймовый дисковод для чтения флоппи-дисков. Я даже написал драйвер для обращения к дисководу и чтения/записи секторов.
IBM PC XT я впервые увидел в лаборатории кафедры транспортного машиностроения Коломенского института МГОУ, где одно время работал Эдик. Мне по знакомству давали посидеть за ним. Тогда это было в диковинку: качество сборки компьютера, клавиатура, монитор стандарта «Геркулес» с черно-белой графикой высокого разрешения. В лаборатории я познакомился с языком Fortran и с DOSом.
Поэтому сомнений, в какую профессию идти, у тебя не было?
Да, я мечтал быть программистом.
Когда ты начал программировать профессионально? Твой первый опыт работы?
В 1999 году, когда заканчивал учебу в университете, меня приняли на работу в АСКОН.
Как ты узнал про компанию, почему решил прийти на работу именно сюда?
Узнал от знакомых. Сначала я обратился в АСКОН на 2 или 3 курсе, но тогда моих знаний для работы не хватило. Я начал изучать язык С, дома уже был 286-й компьютер. Когда почувствовал больше уверенности, пришел во второй раз. На собеседование принес свои наработки: алгоритм разбора алгебраического выражения, программу, рисующую проекции фигур с помощью матриц преобразования.
Видимо, чем-то я понравился, и меня взяли на испытательный срок. Моим наставником стала Татьяна Михайловна Янкина, одна из основателей компании. Первое впечатление было, что я попал в коллектив увлеченных людей. Они работали допоздна по 14 часов в сутки.
Сначала Татьяна Михайловна дала мне хорошую школу индустриального подхода к программированию: основные правила C++, стандарты и требования. Голова распухала от информации. Испытательный срок я прошел за один месяц.
Твоя первая задача в разработке КОМПАС-3D?
Кинематическая операция. На тот момент основным продуктом был КОМПАС-График, а трехмерный КОМПАС-3D только готовился к выходу. Требовалось написать процесс ввода: как пользователь выбирает сечение, выбирает траекторию и получает протягиванием кинематическое тело. Я рассматривал разные ситуации со стыковкой/нестыковкой, когда пользователь совершает ошибочное действие и нужно выдать подсказку. Там были задачи и попроще, а мне дали сразу одну из самых сложных.
Какие работы ты еще делал в КОМПАСе?
Кроме кинематической операции, я сделал конструктивную плоскость. В ней тоже присутствуют разные комбинации и способы построения: по трем точкам, по точке и ребру, по касательной и точке.
После выхода первой трехмерной версии КОМПАС 5.9 нужно было развивать другие направления, не хватало математики. И тогда меня взял к себе Николай Николаевич Голованов.
Первый трехмерный КОМПАС: версия 5.9
Каким ты увидел геометрическое ядро?
Я начал с отладки ошибок, а это очень скучное занятие, но зато проникся устройством ядра, познакомился с его архитектурой. Потом была реализация комбинаций частных случаев пересечения поверхностей, где требуется решение в аналитической форме. В основном это конические сечения: цилиндр с плоскостью, цилиндр с цилиндром, конус с цилиндром. Множество ситуаций, когда на выходе получаются не просто сплайны, а аналитические кривые: окружности, эллипсы, параболы, гиперболы.
Ядро — это больше про математику, а не программирование…
У меня была хороша база по аналитической геометрии благодаря вузу. Все векторно-матричные операции я знал. Чего не хватало, так это знаний по алгоритмам вычисления больших линейных систем уравнений с разреженными матрицами. Здесь большое влияние на меня оказал профессор Рязанского радиотехнического университета Ранас Мударисович Ганеев. Мы использовали метод Гаусса, но у него имелись недостатки — невысокое быстродействие и отсутствие решения для вырожденных матриц. Тогда Анатолий Крючков, как аналитик КОМПАСа и энтузиаст всяких перспективных штук, пригласил профессора Ганеева. Он подобрал для нас алгоритм, основанный на QR-разложении. Я вникал и разными способами внедрял этот алгоритм в солвер. По итогам сделанного мы написали статью в журнал «САПР и графика»
«Решение системы линейных алгебраических уравнений в параметрическом моделировании».
Подойдем к решателю. Когда ты стал им заниматься?
Решатель сам меня нашел. До этого я проработал пересечение поверхностей в геометрическом моделлере, в том числе общий случай пересечения поверхностей, чем заслужил доверие, и мне вручили солвер.
На тот момент в двумерном решателе были большие пробелы, не хватало рук для его развития. В каком-то смысле он был одноклеточным — работал как численный метод: загружалась система уравнений и выдавался ответ. Он не умел справляться с недоопределенными задачами, с системами уравнений, где появлялась вырожденная матрица. Требовалось реализовать метод декомпозиции, разбиение задачи на подзадачи, чтобы надежнее обрабатывать все чертежные случаи.
Объясни, что же такое решатель ограничений (он же солвер)?
Если кратко, то геометрический решатель — это программный модуль, основная задача которого найти такое состояние всем геометрическим объектам, которое удовлетворит все заданные ограничения. Формулируется в одном предложении, но за ним стоит рассмотрение огромного класса случаев. Пользователь может задать какие-угодно ограничения, нарисовать любые контуры и кривые (если брать 2D) и как угодно их друг с другом соединить, выставить любые размеры.
Основное отличие решателя заключается в вариационности подхода: все ограничения равноправны. Постановка задачи идет не процедурным, а декларативным способом. Процедурный подразумевает набор шагов, как, например, в булевых операциях «просверли отверстие, сделай скругление».
Декларативный способ задает конечный результат (хочу, чтобы грани были параллельны), а последовательность действий происходит внутри решателя. Два этих способа не конкурируют, а дополняют друг друга. Об этом хорошо написал Дмитрий Ушаков, CEO Bricsys Technology Russia (ранее CEO ЛЕДАС), в статье на isicad. В САПРе солвер реализует декларативную парадигму, когда пользователь не говорит, что делать, а сразу описывает результат.
Какова роль решателя в параметризации?
Если под параметризацией понимать наделение геометрической модели набором управляющих параметров, то в двумерном мире, в рамках чертежа, роль 2D решателя — центральная: с помощью размеров мы описываем параметрический чертеж.
В трехмерной параметрической модели 3D-решатель обслуживает систему сопряжений, т.е. выполняет задачу позиционирования деталей сборки, а также кинематический анализ.
Если говорить о КОМПАС-3D, то в нем есть еще один решатель — EquSolver, параметрический. Он отвечает за решение систем инженерных уравнений. В нем нет геометрических понятий, а есть переменные, уравнения и операции, вложенные в дерево. Основная фишка: пользователь задает уравнения в таблице одновременно на всю модель, а решатель разбирает, в какой момент, пока он перестраивает, подключить то или иное уравнение. Мы сделали его в 2006 году, аналитиком был Анатолий Крючков, а я отработал математическую модель.
Что было самым сложным в работе над геометрическим решателем за эти 15 лет?
Всегда остаются задачи, которые никогда не могут быть решены полностью. Наверное, труднее других дался метод декомпозиции. Это всевозможные способы распознания в общей задаче мелких подзадач — как превратить сложное в простое. Сначала были неудачные способы, намеки на будущие решения, приходилось делать распознание отдельных мелких ситуаций. Потом они обобщались, и можно было придумать целую вычислительную «машину», которая умеет обрабатывать сразу все ситуации.
В 2012 году математическое подразделение АСКОН было преобразовано в компанию C3D Labs, и постепенно стали появляться внешние заказчики. Как они повлияли на решатель?
Как ни крути, основным поставщиком требований для нас был КОМПАС-3D. Принципиально новые возможности сейчас требуются Приложениям КОМПАСа. До сих пор мы решали задачу сборки, где каждый сопрягаемый объект принадлежит какому-то телу, а предметом вычисления является положение тел в пространстве. От дивизиона Приложений поступила задача, когда присутствуют разнородные объекты, которые могут принадлежать телам (кластерам), а могут быть сами по себе в общем пространстве модели. Это заставило нас реформировать трехмерный решатель.
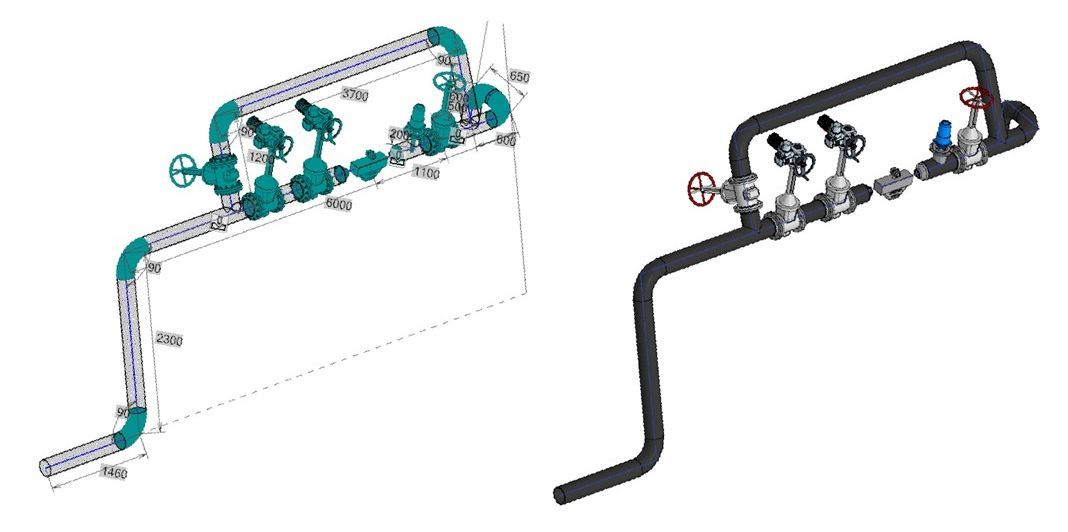
Каркасная модель в приложении Оборудование Трубопроводы для КОМПАС-3D
По запросу «Нанософта» сделали отложенную формулировку ограничений, когда внутренняя система уравнений формируется не в момент добавления ограничений, а в момент запроса на пересчет (вызов Evaluate). Это позволяет распараллелить процесс накачки солвера и формулировать более качественную систему уравнений. Например, решился запрос от «Нанософт» о поддержке нулевых радиусов, когда окружности превращаются в точки. В большей степени это была программная работа, нежели математическая, но внутренности солвера перелопатили здорово.
Наш турецкий заказчик Mubitek раньше использовал другой решатель, D-Cubed, и чтобы ему было проще перейти на C3D Solver, мы подстроились и сделали распараллеливание ввода данных в API, как это принято в D-Cubed.
Так какая же задача в солвере остается нерешенной?
Диагностика нерешаемых задач. Она сделана для большинства случаев и пока удовлетворяет и КОМПАС, и внешних заказчиков, но все равно встречаются еще проблемные ситуации. Речь о том, когда пользователь задает противоречащие ограничения и нужно ему дать информацию, что чему противоречит. Диагностика переопределений остается не решенной в полной мере. Оценить решаемое и нерешаемое — это квинтэссенция геометрических решателей.
Геометрических ядер в мире больше 10, а лицензируемых пять. Решателей же всего четыре. Это еще более высокий уровень сложности, чем геометрическое моделирование. Что нужно, чтобы заниматься решателем?
Знания, опыт, математика, изобретательность. Нигде в учебниках не описано, как решить систему геометрических ограничений в общем виде, зато в математике отработаны численные методы, теория графов, аналитическая геометрия, дифференциальная геометрия, вычислительная геометрия. Главное, что требуется, — уметь соединить все элементы в решающую машину и завести ее.
Математика — абстрактная, отвлеченная наука, но в ней можно найти алгоритмы, применимые к нашим задачам. Например, есть задача на потоки в сетях — распределение потоков по сети трубопроводов в теории графов. Она вроде бы к геометрическому решателю совсем не имеет отношения, но этот алгоритм применяется для распознания жестких структур (кластеров), т.е. в декомпозиции.
Если готовых учебников нет, ты бы взялся написать книгу о геометрическом решателе?
Пожалуй, да. Можно было бы собрать в книге базу знаний, какие подходы, методы, алгоритмы требуются. Что-то вроде «Построй решатель своими руками».