
Три разные по форме геометрические фигуры имеют равные по величине одноимённые константы. Это правильный шестиугольник, овалы стабильной формы циклоп (циклоидальный овал) и треопар (параболический треугольник). А предмет совпадения — площадная контрпрямоугольная константа, равная 0,75. Другими словами, все эти фигуры, вписанные в прямоугольники, займут в них ¾ площади. Это легко доказуемо, как аналитически, так и геометрически. Давайте проверим.
Правильный шестиугольник
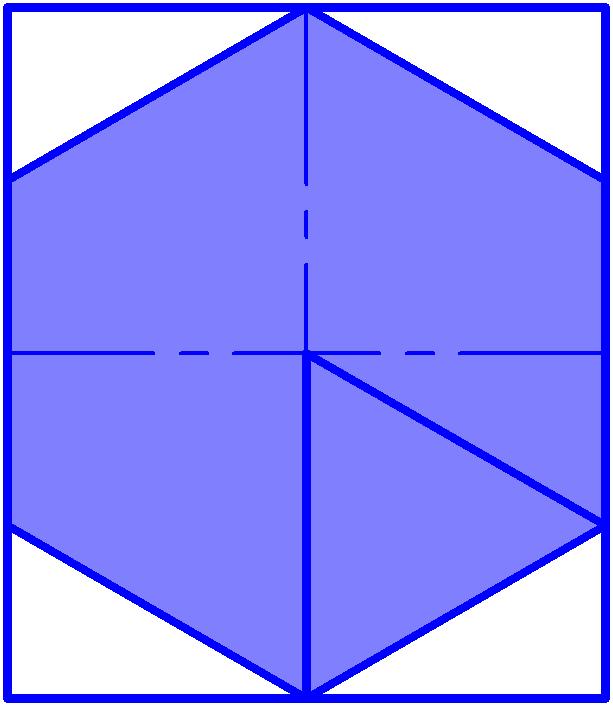
Рис. 1
Разбиваем шестиугольник на шесть правильных треугольников. Определяем площадь одного из них:
Sтр = (a2/4)√3, где a – сторона треугольника.
Площадь шестиугольника:
Sш = (3a2/2)√3 .
Площадь описанного прямоугольника:
S = 2a2√3 .
Составим соотношение площадей шестиугольника и прямоугольника и, выполнив необходимые сокращения, получаем площадную контрпрямоугольную константу: Кш = 3/4.
Циклоп
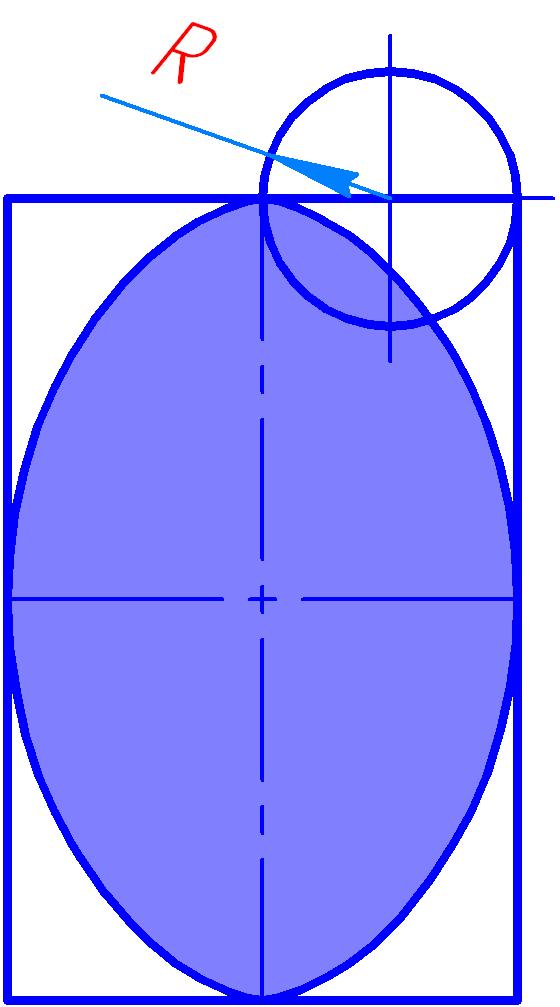
Рис. 2
Фигура образована зеркальной стыковкой двух циклоид.
Эту стыковку впервые осуществил в 17 веке Блез Паскаль. Полученному овалу он посвятил несколько своих работ. На основе овала им созданы и описаны тела вращения, определены площади поверхности и объёмы этих тел.
Автор данной статьи посвятил этому овалу несколько заметок на isicad.ru, предложил новое имя кривой — Циклоп, определил значения ряда констант овала.
Считается, что первым исследователем циклоиды был Николай Кребс (Кузанский), крупнейший немецкий мыслитель 15 века. А настоящий взрыв интереса к этой кривой случился среди учёных 17-18 веков. Анализом кривой занимались: Галилей, Ферма, Декарт, Лейбниц, Ньютон, братья Бернулли и многие другие.
Вернёмся к циклопу и определению его площадной контрпрямоугольной константы. Сначала вычислим площадь овала. Сделать это достаточно просто благодаря экспериментальному доказательству Галилея равенства площади под аркой циклоиды сумме площадей трёх производящих кругов.
Исходя из этого запишем формулу площади циклопа:
Sц = 6πR2 .
Площадь описанного прямоугольника равна произведению осей овала:
Sπ = 8πR2 .
Площадная контрпрямоугольная константа циклопа:
Кц = Sц/Sπ = 3/4 .
Треопар
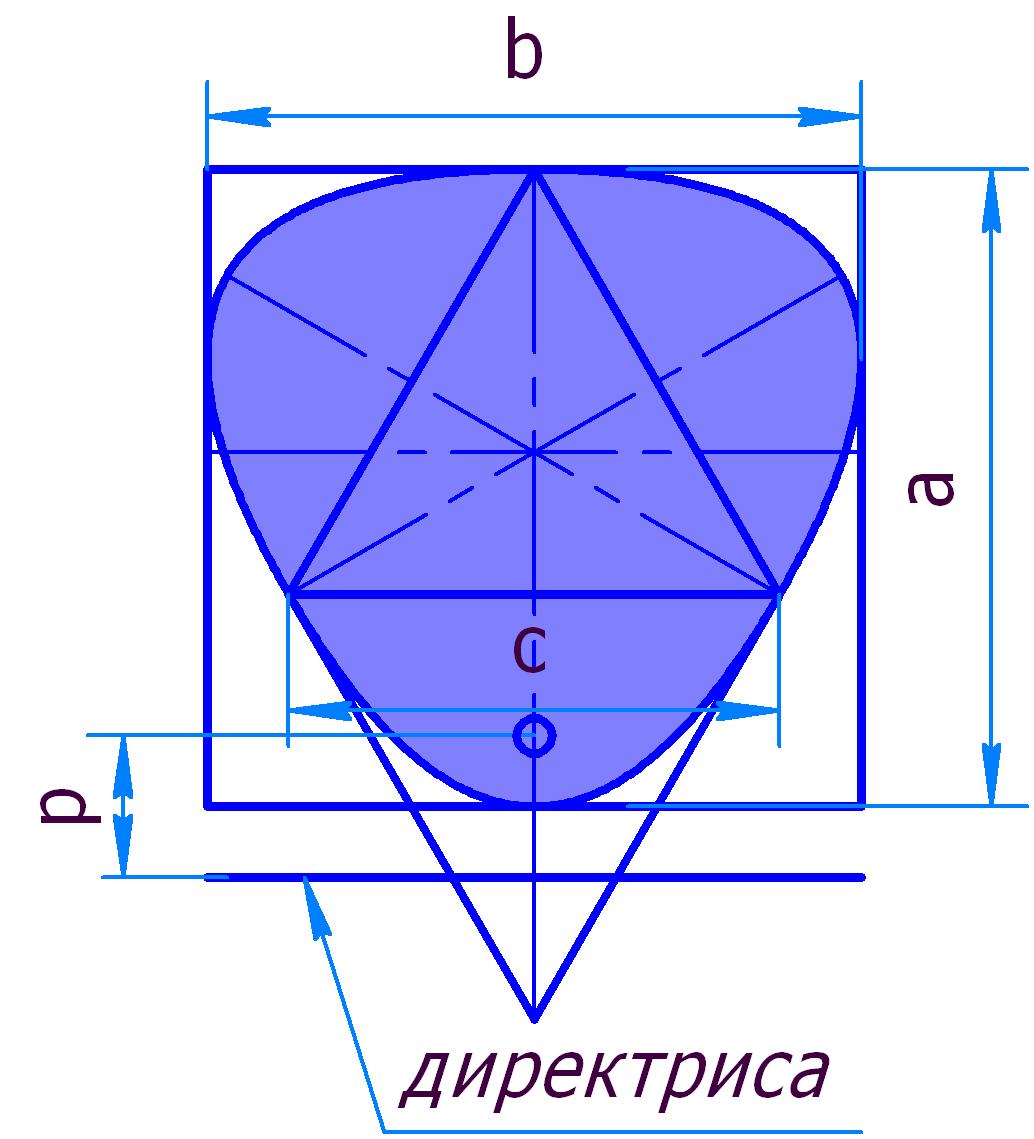
Рис. 3
Треопар — овал стабильной формы, образованный стыковкой трёх парабол.
Сначала определим константы треопара, которые понадобятся в расчётах его площади и контрпрямоугольной константы:
a/p = 4,5; b/p = (8√3)/3; c/p = 2√3, где p – параметр параболы.
Для вычисления площади овала выполним вспомогательные построения:
- соединим соседние точки стыковки отрезками (хордами парабол);
- проведём касательные в точках стыковки к одной из парабол;
- точку пересечения касательных соединим отрезками с концами хорды.
Эти отрезки и хорда образуют равносторонний треугольник. Площадь треугольника:
S = 3p2√3 .
Согласно доказательству Галилея, площадь сегмента параболы, ограниченной хордой, составляет 2/3 от площади данного треугольника. Следовательно, площадь сегмента
S = 2p2√3 .
Площадь треопара, состоящая из 3 сегментов и внутреннего треугольника:
Sтр = 6p2√3 + 3p2√3 = 9p2√3 .
Площадь описанного прямоугольника:
Sпр = 4,5p (8/3)p√3 = 12p2√3 .
Площадная контрпрямоугольная константа треопара:
K = (9p2√3)/(12p2√3)=3/4 ,
что и требовалось доказать, все три фигуры имеют равную константу!
В очередной раз выручает Галилео, спасибо ему! Да и основоположникам геометрии тоже!
Вот и всё, о чём я хотел рассказать.
Вступайте в «Клуб 0,75» сержанта Циклопа 
Всем по 0,75… Шампанского!
Ссылки на публикации автора, посвященные циклопу:
Второе рождение циклоидального овала, или как был разобран по косточкам циклоп
Циклоп. Такой, какой есть
Циклоп с уточнёнными константами и подковами на копытах
Циклоп штурмует фемтометровый диапазон
Вот тебе, Блез, и Циклопов день!
Овалы циклоп и циркон добиваются идеальной формы похудением, в отличие от других