Второе рождение циклоидального овала, или как был разобран по косточкам циклоп

Согласно справке из Википедии, Блез Паска́ль (фр. Blaise Pascal; 1623-1662) — французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.

Предисловие

Так что удивляться не стоит – то, что не знали «древние» стало доступно в 15 – 18 веках. Ту же циклоиду, казалось бы, изучили тогда вдоль и поперёк. Однако белые пятна всё же остались, что также не удивительно.

Рождение новой кривой. 17 век

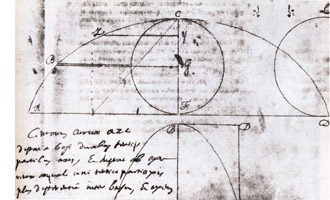
Рис. 1. Фрагмент из работы Блеза Паскаля

Интересно было узнать и имена других ученых, изучавших циклоиду: Галилей, Ньютон, Мерсенн, Декарт, Лейбниц, братья Бернулли, Рен, Ферма, Торичелли, Вивиани, Роберваль, Гюйгенс, Чирнхаус, Лопиталь, Бовель, Николай Кузанский… Согласитесь, список впечатляющий! Однако они не увидели в овале, сложенном из двух циклоид, новую кривую, во всяком случае, не описали её свойств, не нарекли именем.

Второе рождение кривой – вывод из забвения

Циклоида, с её овальными очертаниями, хотя и не принадлежит к замкнутым кривым, тоже попала в поле моего зрения. Когда первая циклоида была мной построена, было замечено, что касательные к кривой в точках возврата не проходят через верхнюю точку производящей окружности, что противоречит одному из свойств циклоиды. Разбиение производящей окружности на большее количество отрезков давали также неутешительные результаты. Тогда возникла идея зеркально отобразить точки построения циклоиды относительно её основания и соединить все точки единым замкнутым сплайном. Полученный таким образом овал состоит из двух кривых, которые уже соответствуют указанному свойству циклоиды. Возможно, и у Паскаля была подобная последовательность действий для получения правильной геометрии циклоиды.

Но кривая, состоящая из двух циклоид, уже интересовала меня больше как овал (что думал по этому поводу Паскаль, мне неизвестно). Это то, что я искал для вышеупомянутой статьи. Первым делом стал смотреть информацию об этом овале в интернете и, ничего кроме картинки Паскаля (рис. 1), не нашёл. Молчок и полный тишок (спасибо Давиду Левину за возрождение забытого слова, а если его и не было, то с лёгкой руки ДЛ будет!).

У геометрической фигуры нет имени, нонсенс, надо исправлять. Первое название было «кривая 2С» (двойная циклоида), затем изменено на «циклоидальный овал». Этот термин впервые предложен в статье [1], в которой и начато описание геометрии и свойств овала, и которое было продолжено в статье «Циклоидальный и псевдоциклоидальные овалы», САПР и графика, №11, 2014 [2].

В одной написанной мной статье было предложено называть циклоидальный овал циклопом. Приживётся ли такое имя, покажет время.

Почему именно циклоп:

1. Имя созвучно с циклоидой;
2. Многие известные геометрические фигуры имеют короткие имена;
3. Своей формой овал похож на беспозвоночное животное из отряда веслоногих ракообразных, называемое циклопом;
4. Провести параллель можно и с мифическим существом – циклопом – одноглазым гигантом. Наш геометрический циклоп отличается не размером, а циклопическим (большим) количеством констант. Вместо глаза у него два фокуса.

Элементы циклоидального овала (циклопа) Рис. 2 и циклоидальных овалоидов

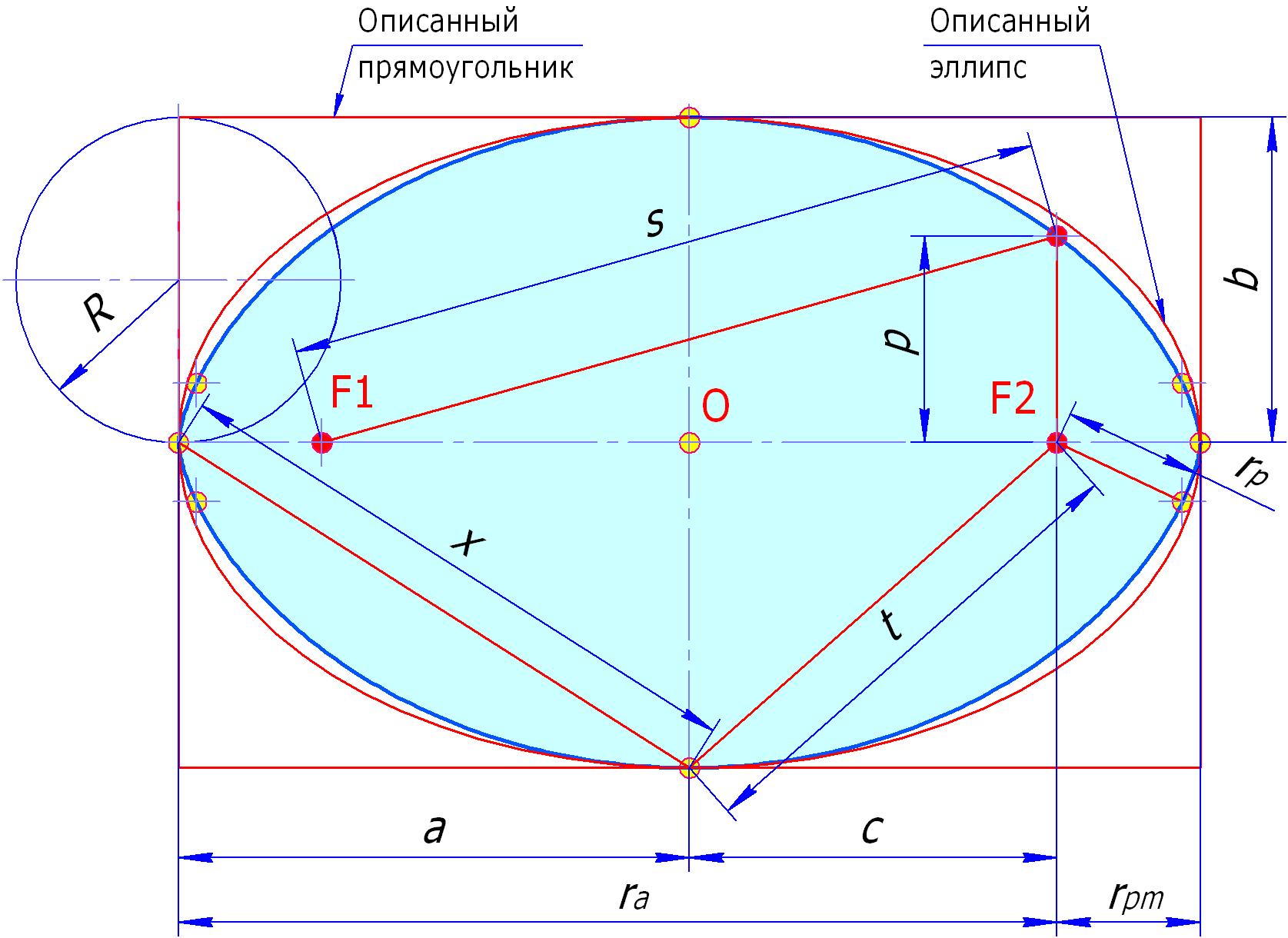
Рис. 2. Циклоидальный овал (циклоп)

Поиск упоминания циклоидального овала и его констант в литературе и интернете ничего не дал, поэтому названия констант и их обозначения предложены автором. Значения констант также пришлось (не без труда, но с интересом) определить самому. Математики, проверьте!

Первые семь констант были приведены в статье [1]. Позже были определены значения ещё девяти констант, семь из которых приведены в статье [2]. В этой статье приводится полный список констант, в том числе, две новые, а значение одной из ранее определённых констант уточнено, это касается перифокусной константы.

Формулы расчета некоторых параметров циклоидального овала и циклоидальных овалоидов:

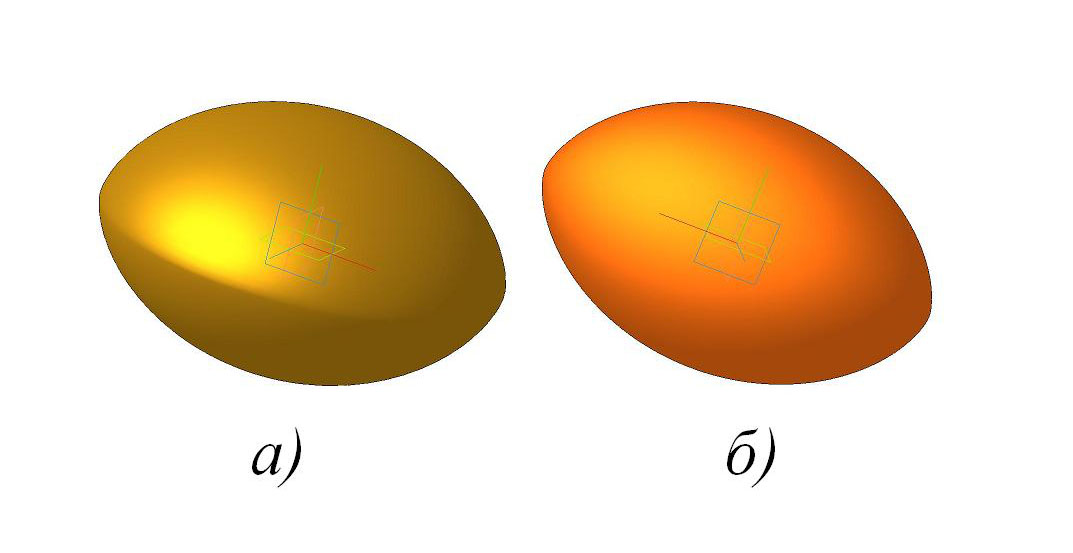
Рис. 3. Циклоидальные овалоиды: а) овалоид вращения вокруг малой оси; овалоид вращения вокруг большой оси

Свойства циклоидального овала

Одним из свойств циклоидального овала является наличие двух фокусов, имеющих строго определенное расположение. Фокусы могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. Это свойство было описано в статьях «А не замахнуться ли нам на Габриеля нашего Ламе?», САПР и графика, №8, 2013 [3] и «Параболический ли купол Исаакиевского собора?», isicad.ru, №127, февраль 2015 [4].. Точки падения этих лучей на кривую, также как у кривой R-1, являются характерными – в них меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный (рисунок с полным комплектом характерных точек не показан).

Отличительным свойством овала является наличие четырёх перицентров. У эллипса, как известно, их два.

Еще одно свойство циклоидального овала (циклопа): размеры элементов овала могут быть найдены как произведение радиуса производящей окружности данной циклоиды или размеров осей (полуосей) с определенными константами, приведенными выше. Это позволяет, зная значение одного (любого) элемента или параметра овала, определить радиус производящей окружности циклоиды и построить овал.

Как видим, циклоидальный овал по своим свойствам и геометрии является уникальной кривой. Взять хотя бы константы. Найдется ли ещё геометрическая фигура с таким количеством констант?

Стоит сказать и о том, что циклоидальный овал является «родоначальником» бесконечного ряда овальных кривых. Присвоим им имя – «псевдоциклоидальные овалы» - (PCO – сокращенное от pseudo-cycloidal oval) и рассмотрим их ниже.

Псевдоциклоидальные овалы (псевдоциклопы)

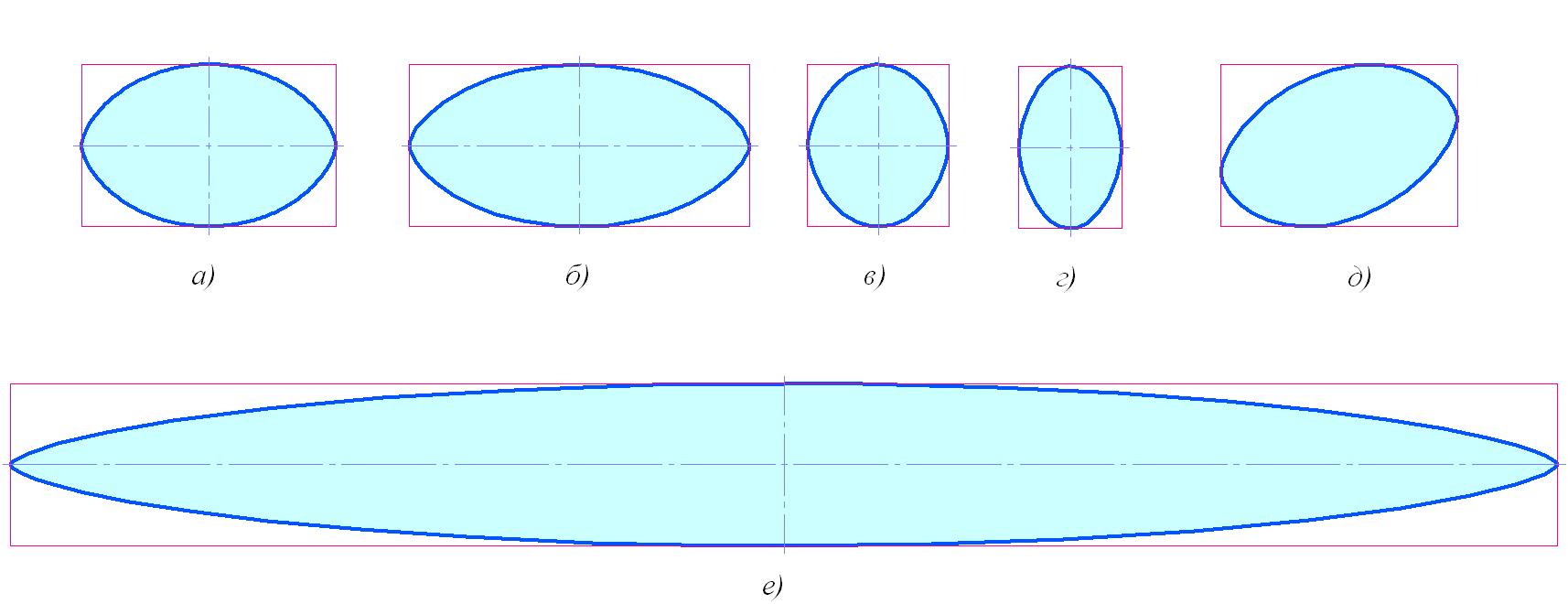
Рис. 4. Овальные кривые: а) циклоидальный овал;
б) и е) – вытянутые псевдоциклоидальные овалы;
в) и г) – сжатые псевдоциклоидальные овалы; д) косой псевдоциклоидальный овал

PCO сохраняют некоторые черты циклоидального овала, как по форме, так и по свойствам (это не касается косых псевдоциклоидальных овалов.) Потеряв большинство констант, две из них PCO всё же сохраняют: это площадная контрэллипсная константа и площадная контрпрямоугольная константа, причём их численные значения совпадают с аналогичными у циклоидального овала:

площадная контрэллипсная константа Spcoe = S/Se ≈ 0,954 929 658 55…;
площадная контрпрямоугольная константа Spco□ = S/S□ = 0,75,

где: S – площадь овала, Se – площадь описанного эллипса, S□ – площадь описанного прямоугольника.

Эти константы помогут идентифицировать PCO из ряда различных овальных кривых.

Псевдоциклоидальные овалы (кроме косых), как правило, имеют по два фокуса, но в определенных интервалах параметров могут быть бесфокусными. В сжатых псевдоциклоидальных овалах, в зависимости от параметров, фокусы могут располагаться как на одной, так и на другой осях. По предложенной в статье [1] классификации эти кривые (кроме косых) – гипоовалы. Сравним площадную контрпрямоугольную константу CO и PCO, равную 0,75, с аналогичной константой окружности и эллипса, у которых она составляет: π /4 ≈ 0,785 398 163 39…. По этой константе циклоидальный и псевдоциклоидальные овалы можно назвать эталонными овальными кривыми.

Применение

Псевдоциклоидальные овалы, благодаря бесконечному разнообразию форм (пропорций), могут быть использованы в таких областях техники, как: кораблестроение, авиастроение, архитектура, оптика и многих других.

На рис. 5 показаны 3D-модели нескольких псевдоциклоидальных овалоидов.

Рис. 5. Псевдоциклоидальные овалоиды. Примеры

Заключение

Прошу проверить и уточнить значения констант (конечно, не до 10-триллионного знака, как это было, да ещё и продолжается, с числом Архимеда). ☺ Особо ценным будет уточнение фокальной константы.

Если у кого-то возникнет вопрос: зачем вообще нужны эти константы, то попробуйте решить такую задачу: необходимо определить площадь циклоидального овала при условии, что известен размер только одного из его элементов (например, перифокусное расстояние). Вопрос после этого, надеюсь, будет снят.

Ответит ли кто-нибудь на вопрос: Являются ли псевдоциклоидальные овалы брахистохронными кривыми? Кто давно не делал открытий, предлагаю заняться!  

Желаю Вам успехов в труде и большого счастья в личной жизни!.... Благодарю за внимание! (Фраза заимствована у прораба – лектора (М. Пуговкин) из «Операции Ы»).  

Библиографический список