
Не умею и не люблю писать большие статьи, равно как и читать такие, за редким исключением. Вот и эта заметка будет не длинной – это краткое сообщение, дополняющее материал предыдущей заметки о задаче Томсона.
Будет продолжение или нет, не сразу было решено. Но в данном случае отказаться от продолжения исследования означало бы бросить начатое на половине пути и не узнать, а что там при N = 10 и после N = 12, – этого я не мог себе позволить.
Начну с удивления тому факту, что правильный додекаэдр до сих пор не считался решением задачи Томсона или, возможно, что такое решение не было доказано. Но какие нужны доказательства? Многогранник имеет 20 вершин, равномерно разнесённых по поверхности описанной сферы – рёбра, сходящиеся в вершинах, имеют одинаковую длину. Кроме того, из всех многогранников, имеющих 20 вершин, додекаэдр обладает максимальным значением отношения своего объёма к объёму, ограниченному описанной сферой (0,664760…).
Итак, по моему мнению, решениями задачи Томсона являются четыре тела Платона: тетраэдр, октаэдр, икосаэдр и додекаэдр. Они являются экстремальными в смысле максимального разнесения вершин на сфере для N = 4, 6, 12 и 20.
Резонно возникает вопрос: а какие многогранники являются экстремальными для остальных N в диапазоне от 6 до 20?
В упомянутой выше заметке определён такой многогранник для N = 8, это – простая квадратная антипризма. Выяснилось также, что октаэдр одновременно является треугольной антипризмой. Это позволяет предположить возможность существования антипризм, являющихся экстремальными многогранниками и для других значений N.
Для проверки этого предположения были построены 3D-модели многогранников с N = 10 и 14 в форме простых пятиугольной и семиугольной антипризм, с отношением высоты к радиусу описанной окружности основания, равным √2. Это значение гарантирует максимальный объём антипризмы, вписанной в сферу.
Для реализации «Метода соотношений объёмов», который впервые был использован для определения экстремального многогранника с N = 8, рассчитан объём описанной сферы по формуле:
V = 4/3 π (√(3r^2/2))^3,
где r – радиус описанной окружности основания антипризмы.
Объём антипризмы брался из МЦХ соответствующей модели.
Полученные значения объёмов антипризм с N = 10 и N = 14 были сравнены с аналогичными значениями для других многогранников с теми же N. Результаты сравнения подтвердили предположение – эти антипризмы являются экстремальными многогранниками.
На рис. 1, показанном ниже, приведены графики отношений объёмов многогранник/сфера для экстремальных многогранников: тел Платона и антипризм.
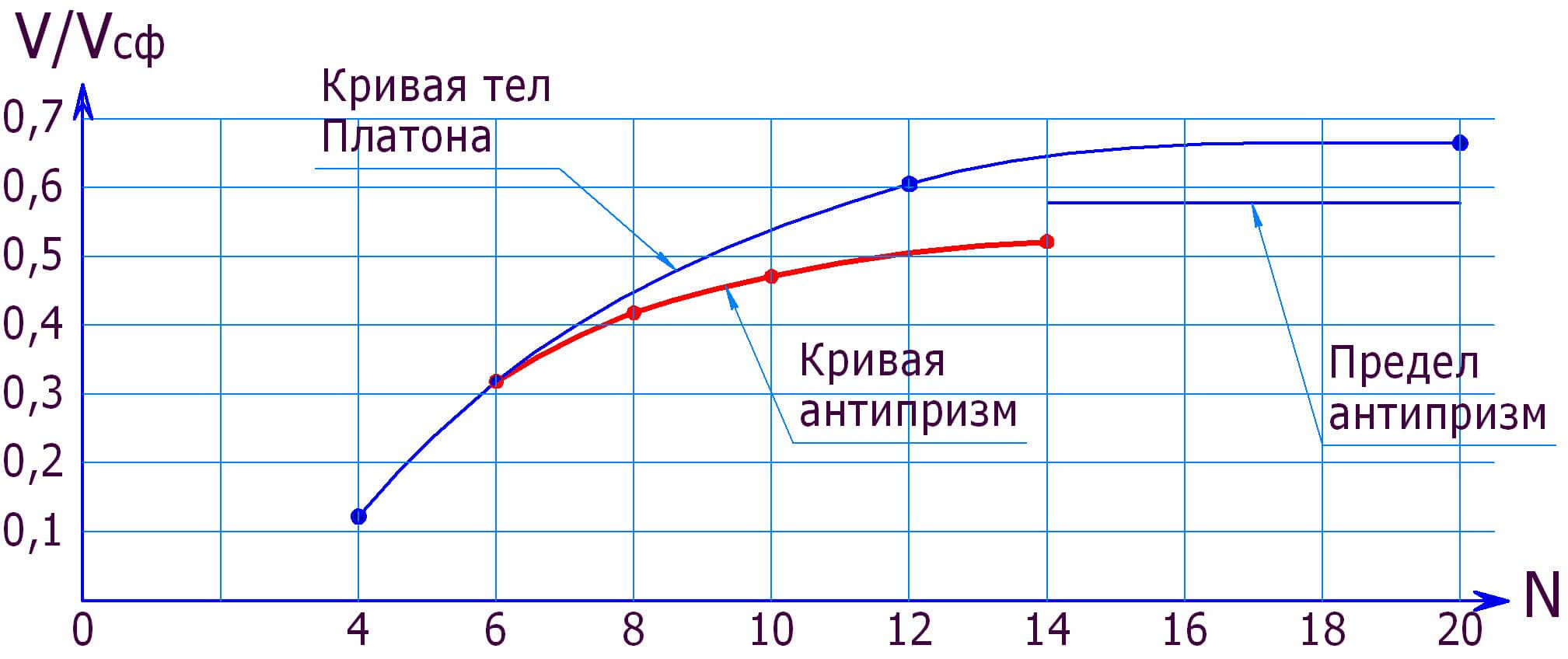
Рис. 1
Модели антипризм были построены для N = 6, 8, 10 и 14. Для N = 16, 18 и далее модели не строились, поскольку есть уверенность, что антипризмы и там будут побеждать. Однако их предел – 0,577350…. Это максимальное по величине отношение объёмов цилиндра и описанной сферы.
Результаты расчётов отношений объёмов экстремальных многогранников к объёмам описанных сфер приведены в таблице ниже.
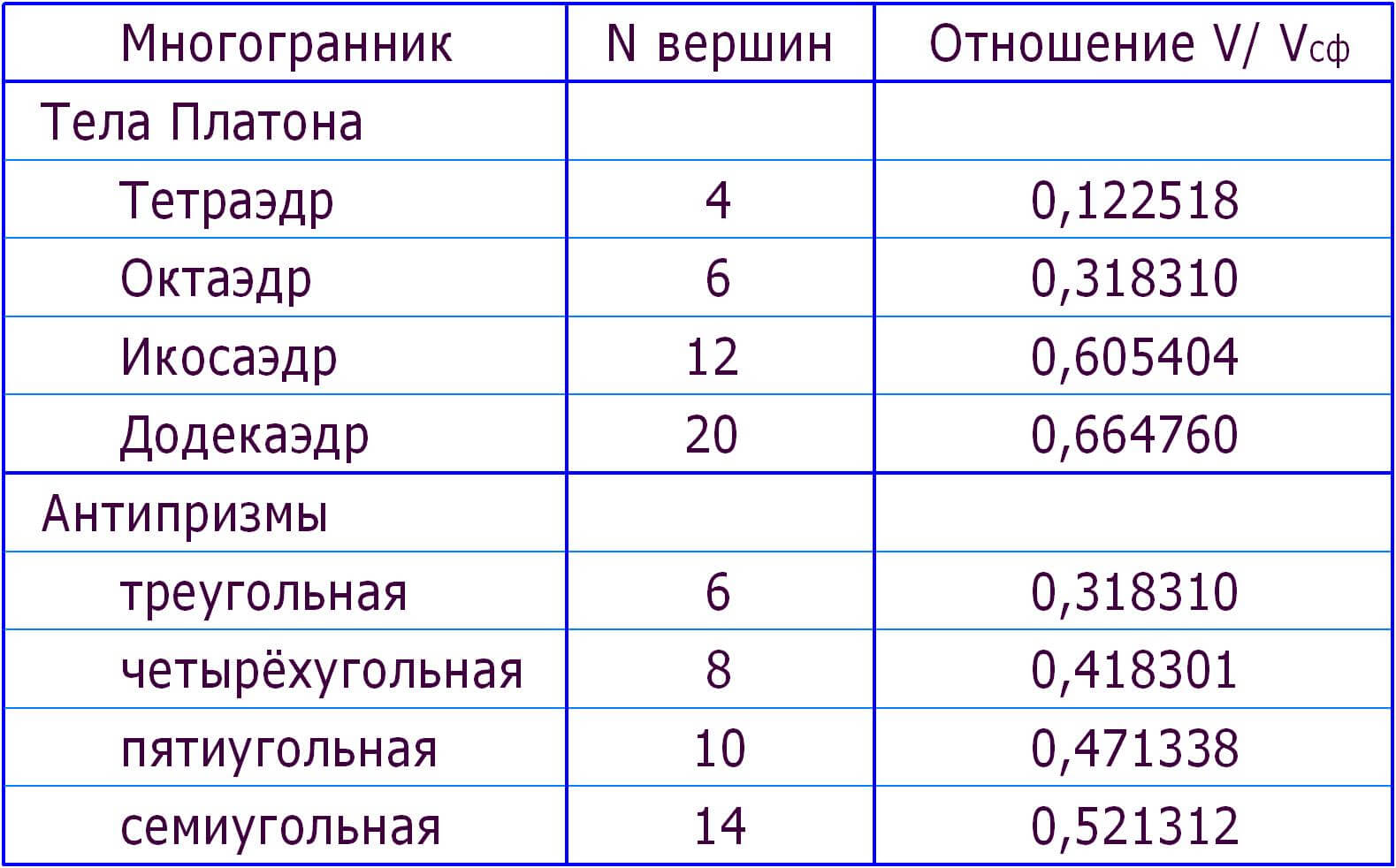
- Все перечисленные многогранники выпуклые.
- Все их вершины лежат на поверхности описанных сфер.
- Количество рёбер, сходящихся в каждой вершине любого такого многогранника, одинаково.
- Одинакова и суммарная длина этих рёбер.
- Суммарная длина связей любой вершины с остальными вершинами многогранника есть величина постоянная.
- Многогранники занимают максимальный (для данного N) объём в описанных сферах.
В заключение хочу подчеркнуть, что других многогранников с чётными N в качестве экстремальных в этом диапазоне не наблюдалось. Их нет, или я плохо вижу со своей «низкой каланчи»? 
На этом я хотел закончить свои изыскания решений задачи, но, просматривая в очередной раз материалы по задаче Томсона, увидел в Интернете статью Л.А. Козинкина «Метод прямого статистического моделирования в задаче Томсона». Опубликована она в «Вестнике Сибирского государственного аэрокосмического университета им. М.Ф. Решетнёва» (предположительно в 2010 году). Вот её аннотация: «Представлены минимальные и равновесные конфигурации систем зарядов на сфере, найденные с помощью метода Монте-Карло. Приведён анализ впервые полученных в ходе работы результатов».
Начал читать статью, а там автор упоминает какие-то ПО незнакомые, не говоря уже о методах мудрёных. Ну, думаю, зря я полез в эту тему, не с моим уровнем с этим всем разбираться. Предположил, что заметку свою с «примитивным» методом соотношений объёмов в лучшем случае придётся переделывать, а то и в корзину её…, по параболической траектории 
Читаю дальше, дохожу до результатов. Обратил внимание на то, что решаются все варианты подряд, в том числе с нечётными N – круто, на первый взгляд, но немного подозрительно. Кстати, к нечётным N я даже подступаться не собирался, боясь потерпеть фиаско.
Дошёл до N = 10, и… неужели ошибка?!
Приведу результаты исследований из статьи, начиная с N = 10 до N = 20, опуская нечётные N:
| 10 | Два заряда на полюсах, остальные заряды образуют антипризму, равноудаленную основаниями от полюсов |
| 12 | Правильный икосаэдр |
| 14 | Два заряда на полюсах, остальные образуют шестиугольную антипризму с основаниями, равноудаленными от полюсов |
| 16 | Равновесная конфигурация с антипризматическими основаниями северного и южного полюсов |
| 18 | Антипризматически расположенные правильные пирамиды с квадратом в основании и одинаково ориентированные пирамиды с неправильными одинаковыми прямоугольниками |
| 20 | Более устойчивая, чем додекаэдр, конфигурация |
Для того чтобы оценить конфигурацию для N = 10, предложенную Л. Козинкиным, была построена модель такого многогранника. Практически это выполнено было так: к основаниям простой квадратной антипризмы (а это – решение для N = 8) были приклеены две четырёхугольные пирамиды нужной высоты (рис. 2а). На этом же рисунке показана модель пятиугольной антипризмы – конкурента по решению задачи (рис. 2б).
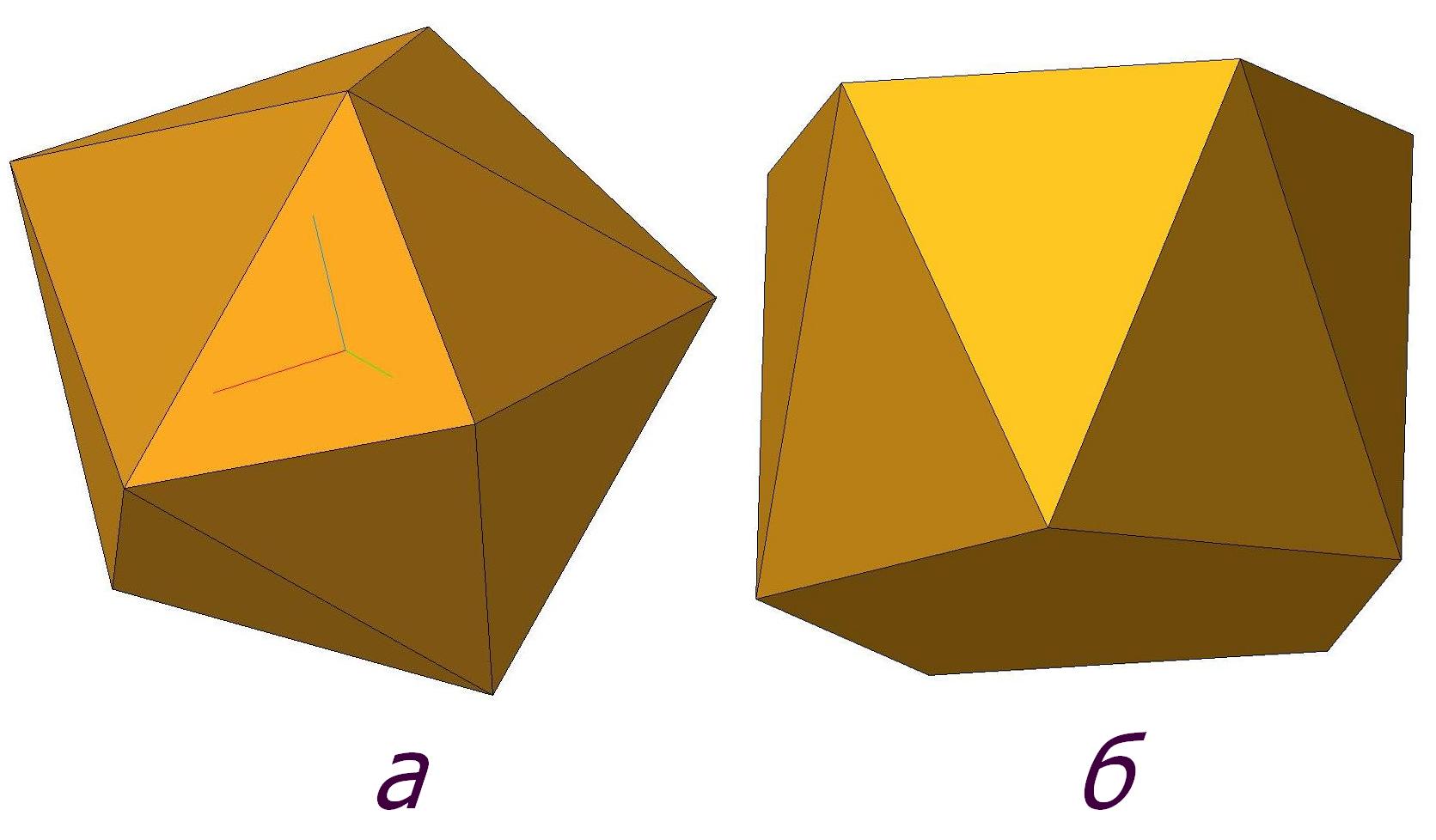
Рис. 2
Но это – не главная причина отказаться признать этот многогранник экстремальным, а соответствующую систему – равновесной. Обратите внимание на рёбра полярных и остальных вершин. У первых вершин их по четыре, у остальных – по пять, а суммарная длина рёбер, сходящихся в тех и других, разнится почти в два раза. Тут ни о каком равновесии системы и равномерности разнесения вершин речи быть не может. Не поможет также использование в качестве базы многогранника однородной антипризмы (по примеру икосаэдра), поскольку рёбер полярным вершинам это не добавляет. Поэтому однозначно: экстремальный многогранник для N = 10 – пятиугольная антипризма.
Конфигурацию из 14 точек автор предлагает строить аналогично, только уже на базе шестиугольной антипризмы и двух точек на полюсах. Этот многогранник будет таким же ущербным, как и предыдущий, по тем же причинам, с той лишь разницей, что у полярных вершин окажутся лишние рёбра. Строить такую модель не имеет смысла.
Конфигурации для N = 16 и 18 описаны туманно, с какими-то непонятными антипризматическими основаниями, что не позволяет представить модели и построить их.
Последний результат приведённой статьи для N = 20 не раскрывает сути: непонятно, что это за конфигурация – более устойчивая, чем додекаэдр?
Итак, переделывать заметку не придётся, и я по-прежнему считаю простые антипризмы экстремальными многогранниками для N = 6, 8, 10, 14 и т. д. А метод соотношений объёмов оказался совсем не плохим, не «Монте-Карло», конечно… 
Вот такое отступление получилось в связи с почти случайным (но полезным) прочтением этой статьи.
Закончу заметку словами из песни В. Высоцкого:
Мы антиподы, мы здесь живём,
У нас тут анти, анти, антиординаты,
Стоим на пятках твёрдо мы и на своём,
Кто не на пятках, те антипяты.
Благодарю за внимание!

