Полигональное моделирование: от фундамента к продвинутым алгоритмам

Автор представляет обзор топологии полигональной сетки, делится информацией об усовершенствованиях и новом функционале, а также знакомит с планами развития направления полигонального моделирования.

Для работы большинства алгоритмов недостаточно иметь представление о сетке только как о наборе треугольников, примером чего служит результат ее конвертации из формата STL. Единственное, что можно сделать с такой сеткой, — это нарисовать ее и посчитать площадь. Для всего остального в нашем распоряжении должна быть некая топологическая структура, которая и является фундаментом в полигональном моделировании.

Эта структура содержит две основные составляющие. Во-первых, это топология сетки, которая описывает связи между вершинами, ребрами и полигонами. Она должна поддерживать не только треугольники, но и полигоны с произвольным числом сторон, или фасеты. Кроме того, в зоне ее ответственности — обеспечение ряда базовых элементарных операций над ними, например, таких, как упорядоченный обход фасетов соседних с выбранным, упорядоченный обход веера вершины, коллапс ребра, вставка вершины, переброс ребра и некоторых других.

Как правило, сетка интересна не столько сама по себе, сколько вместе с неким логическим разбиением фасетов на группы. Отсюда возникает вторая составляющая топологии — сегментация. По структуре она аналогична стандартной B-rep-модели: те же грани, циклы и ребра, только гранями являются связанные группы фасетов, а ребра составлены из последовательностей ребер сетки. Здесь также необходим набор базовых операций по аналогии с топологией сетки, а именно разнообразный обход соседних сегментов, создание новой сегментации или разбиение существующей заданным набором ребер или фасетов, объединение одного или нескольких сегментов, переброска граничных фасетов из одного сегмента в другой и т. п.

Иллюстрация демонстрирует разбиение существующей сегментации. Разные сегменты подсвечены разными цветами, заданными набором ребер, который обозначен желтой полилинией. Второе изображение — результат такого разбиения. Кроме этого, каждому топологическому элементу необходимо поставить в соответствие некий абстрактный атрибут — это может быть число, вектор, поверхность, произвольная структура.

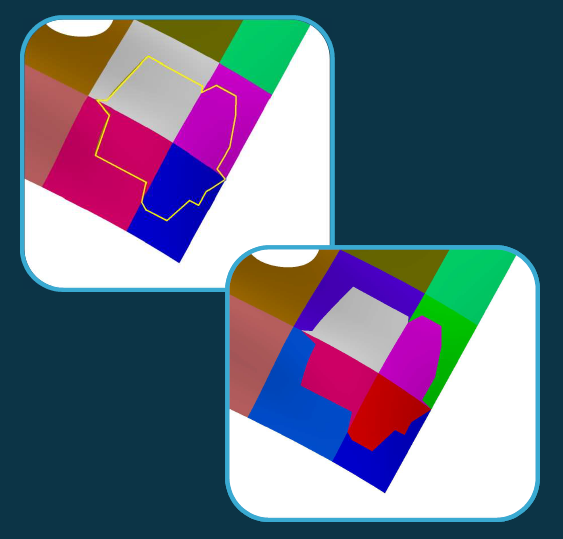
Рис. 1

На первый взгляд, все, о чем шла речь, это давно известные факты, которые кажутся весьма простыми для имплементации. Однако если учесть все разнообразие алгоритмов, которое складывается из этих базовых операций как из кубиков, то оказывается, что это весьма ответственная часть работы, к которой надо относиться максимально серьезно. Особенно если брать в расчет необходимость поддержки актуальности и валидности топологической информации на каждом этапе алгоритма. Зато в результате мы получаем мощный универсальный инструмент, отталкиваясь от которого как от фундамента, можно решать любые задачи в области полигонального моделирования. На данный момент мы являемся полностью самодостаточными разработчиками в полигональном моделировании и не опираемся ни на какие сторонние или open source-решения или продукты.

Рассмотрим результаты, полученные с применением такого системного подхода. Глобально мы наблюдаем улучшение всего имеющегося функционала, преимущественно — ускорение. Базовое лечение сетки на сегодня сводится к созданию топологии. На этом этапе устраняются наиболее очевидные проблемы: дублированные вершины, вырожденные треугольники, дублированные треугольники, неконсистентные нормали. Помимо этого, отслеживаются разного рода неманифолдности. Булевы операции и 3D-выпуклая оболочка были ускорены до 30-40 раз соответственно. Чем больше сетка — тем больше ускорение. Такие операции, как поиск открытых границ или границ связных частей заданного набора фасетов, становятся практически тривиальными. На иллюстрации — лечение сетки с неконсистентными нормалями. На первом рисунке каждый треугольник перевернут относительно соседей, а на втором — результат приведения сетки к нормальному виду.

Рис. 2

Новый функционал объединяет добавление 2D-выпуклой оболочки, упрощение триангуляции, параметризацию сеток, вписывание NURBS-поверхности и аналитических поверхностей в набор полигонов.

На данной иллюстрации мы видим, что все точки триангуляции спроецированы на плоскость, и синим цветом обозначена выпуклая оболочка. Если она есть в наличии, можно построить минимально описанный прямоугольник.

Рис. 3

В случае с упрощением триангуляции возможны два варианта: упрощение до заданного количества треугольников или до достижения заданной точности. Вместе с тем есть возможность получить набор упрощенных сеток с разным уровнем детализации. Упрощение представляет собой последовательность коллапсов ребер, то есть базовой операции, упомянутой вначале. При этом запрещен ряд коллапсов, например, тот, который может привести к сшивке двух треугольников по двум ребрам, схлопыванию открытого контура и т. д. Это гарантирует сохранение топологических свойств полигонального объекта. Если он был подобен диску — он таким и останется, если на нем было n контуров или n ручек, это число также останется неизменным.

На иллюстрациях наглядно показан набор сеток разной степени детализации. К примеру, на последнем из серии рисунков бегемотик симплифицирован до состояния тетраэдра. Его дальнейшая симплификация невозможна без нарушения топологических свойств.

Рис. 4

Данное изображение — пример симплификации сетки более сложной топологический структуры.

Рис. 5

Несмотря на то что параметризация сеток пока не присутствует в API, она является одним из основных инструментов меш-процессинга. Проанализируем этот сегмент на примере модели, в качестве которой выбрано лицо Наполеона, взятое из открытых источников.

Рис. 6

В самом упрощенном виде возможны два случая — параметризация со свободной границей и параметризация с фиксированной границей. Под параметризацией мы понимаем отображение сетки на плоскость. Параметризация со свободной границей — самый общий случай и самый вычислительно сложный. Задача алгоритма — придумать 2D-координаты для каждой вершины сетки. Топологически она должна быть подобна диску. Изображение — результат работы алгоритма.

Рис. 7

На плоскости лицо выглядит так, как на рисунке слева. Наиболее известное применение параметризации сеток — натягивание структуры на поверхность сложной формы. Если в 2D мы нарисуем регулярную прямоугольную сетку, то в 3D она будет выглядеть так, как на рисунке справа.

Параметризация с фиксированной границей — более простой вариант. Для граничных вершин задаем 2D-координаты из неких соображений, а для внутренних — вычисляем. В общем случае, когда ничего неизвестно, можно остановиться на отображении на круге. Лицо на круге выглядит как на рисунке слева, справа — иллюстрация в 3D.

Рис. 8

Если имеются некие априорные знания о сетке, как в данном случае, мы понимаем, что на открытом контуре есть четыре угла, и можем отобразить лицо на прямоугольник. Формально это самый предпочтительный вариант, и результат представлен на картинке.

Рис. 9

Однако у такого подхода есть границы применения. Возьмем сетку более сложной формы, такую, как, например, Стэнфордский кролик. Рисунок слева — то, как он выглядит при отображении на круг. Параметризация крайне неравномерная: внизу квадратики маленькие, вверху — большие. Следовательно, нужно придумывать какие-то другие методы.

Рис. 10

В таком разделе, как вписывание NURBS-поверхности, возможен автоматический подбор узлового вектора. Входными данными являются набор треугольников, порядок сплайна, максимально разрешенное количество контрольных точек, коэффициент сглаживания и желаемая точность, в которую мы стараемся уложиться. Вписывание NURBS-поверхности основано именно на параметризации сеток. Она подсказывает, какие 2D-параметры должны быть у вершин, а имея 2D-параметры, мы можем осуществить аппроксимацию поверхности.

Эта иллюстрация демонстрирует результаты для разных стратегий параметризации.

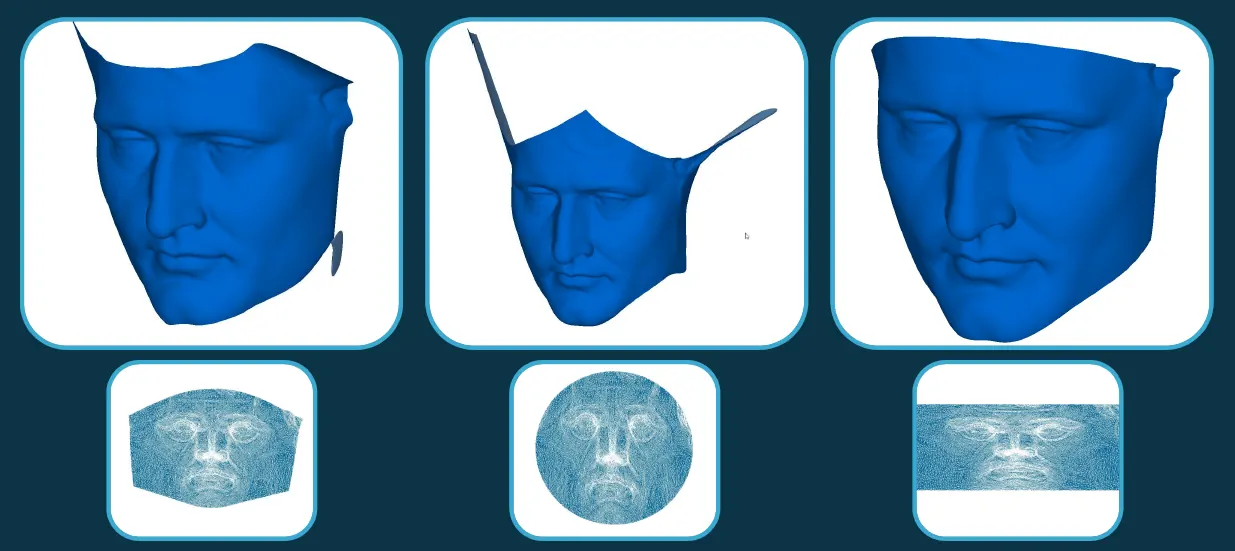
Рис. 11

Слева — самый общий вариант параметризации с открытой границей. Видно, что поверхность хорошо совпадает с сеткой в тех местах, где она есть, и определенным образом ведет себя там, где ее нет. Отображение на круг — естественно, наименее желательный случай. При этом использование некоторой априорной информации о сетке обеспечивает наиболее приемлемый результат.

Далее проиллюстрирована сеть контрольных точек получившейся поверхности.

Рис. 12

На следующем изображении — влияние степени сглаживания. Слева направо степень сглаживания уменьшается.

Рис. 13

Опять же этот подход имеет ограниченные области применения. К примеру, если попытаться представить одной поверхностью кролика, то получится совершенно неудовлетворительный результат, а значит, нужно искать другие пути.

Рис. 14

Что касается вписывания аналитических поверхностей методом наименьших квадратов, здесь тоже имеются варианты, а именно вписывание поверхности заданного типа, либо ее автоопределение. Возможность отбраковки выбросов по разным критериям, а также некий контроль формы, направленный на то, чтобы не создавать поверхности, близкие к вырожденным, например, почти плоские или почти цилиндрические конусы. Входными данными здесь также являются набор треугольников и желаемая точность. Только в этом случае точность используется исключительно для контроля результата в формате «уложились-не уложились».

На следующих слайдах — примеры вписывания разных примитивов. Плоскость:

Рис. 15

Цилиндр, вписанный в сетку довольно плохого качества:

Рис. 16

Далее представлен сектор цилиндра:

Рис. 17

Эта иллюстрация подтверждает необходимость отбраковки выбросов. Обратите внимание на артефакты, расположенные слева внизу на сетке. Если учитывать их при вписывании, они обязательно дадут какой-то систематический сдвиг. Система отбраковки позволяет избавиться от них и получить более качественный результат.

На этом рисунке — пример вписывания сферы.

Рис. 18

Это — конус.

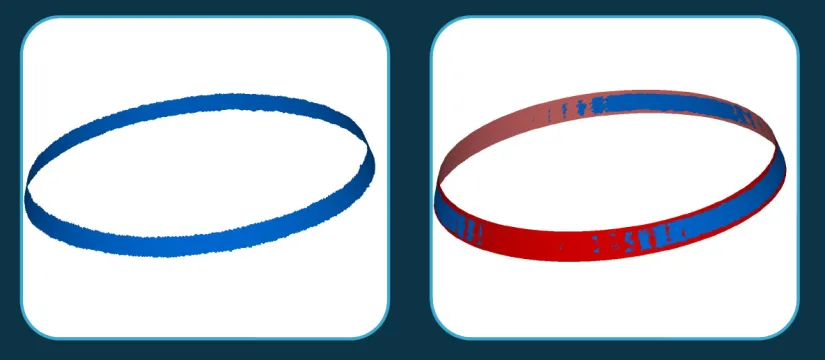
Рис. 19

Это — тор.

Рис. 20

Таким образом мы покрываем все виды аналитических примитивов.

Пару слов о B-Shaper. Концептуально он не изменился, но был несколько обновлен, в частности, его функционал был переведен на новую топологию. Кроме того, были использованы новые алгоритмы вписывания. Это позволило улучшить работу со швами замкнутых поверхностей и оптимизировать ряд других процессов.

Планы в области B-Shaper касаются, в первую очередь, формирования специального подхода к скан-сеткам. Известно, что любой автоматический алгоритм не дает на них удовлетворительных результатов. Еще одна ключевая задача — развитие полуавтоматического реверса с интерактивной сегментацией и с подсказками пользователям. Следующая цель — распознавание кинематических поверхностей. На данном этапе инструмент включает распознавание поверхностей вращения, но его необходимо оптимизировать и дополнить распознаванием поверхностей выдавливания, или экструзии. Не менее важная задача — автоматическая генерация сети из NURBS-патчей. Это необходимо, чтобы в параметрическом виде представлять сложные поверхности наподобие того же Стэнфордского кролика.

В планах в области полигонального моделирования — вписывание поверхностей с учетом ограничений. Например, когда требуется вписать не просто цилиндр, а цилиндр, ось которого должна быть перпендикулярна заданной плоскости. В отношении диагностики и лечения сеток также есть планы. Как правило, базового лечения недостаточно. На сетке могут быть совершенно разнообразные проблемы — зазоры, дырки, самопересечения, топологические дефекты. Важно иметь функционал для эффективных диагностики и лечения. В перспективе — регистрация или совмещение сеток и облаков, которые находятся в разных системах координат. Это важно для того же самого контроля, чтобы определять, насколько хорошо была сделана та или иная деталь. Предположим, у нас есть сама деталь в параметрическом виде и есть набор точек, полученных сканированием. Надо их совместить и спроецировать одно на другое. Список задач также включает дальнейшее развитие булевых операций и представление в API уже существующих алгоритмов, которые сейчас там не представлены, но используются на отдельных внутренних стадиях. Например, сегментация по острым сломам, сглаживание сетки или оценка разных параметров поверхностей по сетке, в том числе кривизн.

Слева на иллюстрации мы можем увидеть направление главных кривизн, оцененных по триангуляции, справа — направление нормалей.

Рис. 21