Технологии вариационного проектирования для разработки типичных приложений САПР

Стратегия компании ЛЕДАС

В статье представлена стратегия компании ЛЕДАС по разработке функционально полных наборов вычислительных программных модулей для разработчиков систем автоматизированного проектирования (САПР). Программные модули компании ЛЕДАС представляют собой библиотеки с реализацией основных функций, необходимых для поддержки вариационного подхода к проектированию в различных конечно-пользовательских программных приложениях автоматизированного проектирования и инженерного анализа. В статье описываются основные преимущества вариационного подхода перед традиционным параметрическим проектированием, основанным на истории построения модели. Описание геометрического решателя, лежащего в основе вариационного подхода, сопровождается комментариями по его использованию для разработки типичных приложений САПР. При описании базовой функциональности таких приложений как эскизное черчение, трехмерное моделирование, проектирование сборок, анализ кинематики механизмов объясняются достоинства, которые обеспечивает вариационный подход для конечных пользователей. Статья завершается кратким перечислением возможных плодотворных приложений вариационного подхода в различных областях знаний.

Параметрическое проектирование: вариационный подход

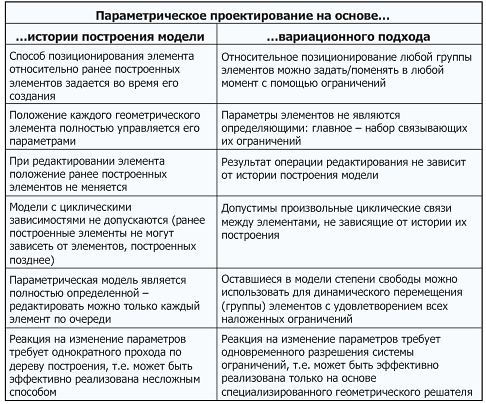
Таблица 1. Два подхода к параметрическому проектированию

Конечно, следует отметить основной недостаток вариационного подхода – при его реализации в САПР приходится иметь дело с одновременным разрешением системы ограничений (уравнений, связывающих параметры конструктивных элементов). Здесь при использовании традиционных численных методов решения систем уравнений возникает ряд известных проблем: недостаточная масштабируемость (время решения растет значительно быстрее размера модели), ненатуральность (найденное решение не соответствует прагматическим ожиданиям пользователя), отсутствие гарантии решения. Следует отметить, что проблемы разрешения геометрических ограничений изучаются научно-исследовательскими группами по всему миру еще с 1960-х годов. За это время был разработан ряд алгоритмов, позволяющих успешно декомпозировать задачи с большим количество ограничений на совокупность простых подзадач и моделировать каждую из них самым эффективным образом. Разработки компании ЛЕДАС на эту тему базируются как на работах Лаборатории искусственного интеллекта Института систем информатики им. А.П. Ершова Сибирского отделения Российской академии наук, так и на собственных исследованиях, которые компания проводила последние восемь лет. Результатом этих исследований стала разработка собственного геометрического решателя LGS, который служит основой для эффективной реализации вариационного подхода в коммерческих САПР.

Вариационный геометрический решатель

Основные объекты решателя – это планиметрические или стереометрические геометрические элементы – точка, бесконечная прямая и плоскость, окружность, цилиндр, сфера, конус и т.п. Допускается также задание произвольных пользовательских кривых и поверхностей (в т.ч. кусочно-гладких и сплайновых). Положения некоторых объектов на плоскости/в пространстве можно зафиксировать абсолютно или относительно (по отношению к группе других объектов). Между объектами можно задавать ограничения – инцидентности, касания, параллельности, перпендикулярности, концентричности и т.п. Кроме вышеприведенных логических ограничений допускаются и параметрические ограничения – расстояние, радиус, угол. Параметры этих ограничений можно изменять.

Дополнительно к геометрическим объектам и ограничениям можно задать свободные параметры и переменные-измерения (величины которых вычисляются по положению геометрических элементов), связав их уравнениями, неравенствами и табличными зависимостями. В уравнениях и неравенствах можно использовать как стандартные математические функции, так и произвольные – определенные пользователем или приложением.

Базовая функциональность вариационного геометрического решателя LGS состоит в удовлетворении наложенных ограничений, т.е. размещении объектов на плоскости/в пространстве таким образом, чтобы удовлетворялись все наложенные ограничения (или максимально возможное их количество). Решатель находит самое натуральное из всех возможных решений задачи: новые координаты объектов должны быть как можно ближе к исходным, начальная ориентация объектов по отношению друг к другу должна быть сохранена.

Важной дополнительной функциональностью является возможность диагностики задачи, т.е. выявлению переопределенных («лишних») и несовместных ограничений, которая позволяет пользователю приложений, созданных на основе LGS увидеть и исправить ошибки в спецификации изделия.

Динамическое перемещение объектов (или динамическое изменение параметров) состоит в нахождении такой траектории движения, в каждой точке которой удовлетворяются все наложенные ограничения. Данная функциональность важна в контексте многих приложений, но особенно – эскизного черчения, проектирования сборок и анализа кинематики. Дополнительные модули к решателю LGS (как уже существующие, так и планируемые к разработке) включают в себя возможности по моделированию объектов более высокого уровня: кинематических пар, плоских профилей, объемных тел, а также выполняют ряд сервисных функций: осуществляют расчет интегральных параметров модели (длин, площадей, объемов, центров масс и тензоров инерции), определяют пересечения объемов и реализуют различные оптимизационные алгоритмы. Таким образом, формируется полный портфель предложений компании ЛЕДАС для разработчиков САПР, позволяющий строить конкретное приложение на основе готовых программных блоков.

Особенности разработки приложений с вариационной функциональностью

Конечно, полноценное геометрическое приложение всегда строится вокруг ядра геометрического моделирования, с помощью которого можно создавать геометрические формы «с нуля». Такое ядро реализует базовые типы и операции, необходимые любому разработчику САПР, моделирует геометрию и топологию объемных моделей на основе граничного представления (BRep), реализует операции по созданию и модификации трехмерных форм, включает модули для триангуляции сложной поверхности, удаления невидимых линий и рендеринга, а также поддерживают чтение и запись геометрических файлов популярных форматов. На рынке доступно несколько популярных геометрических ядер, поэтому компания ЛЕДАС разработала специальную технологию, облегчающую интеграцию своих вычислительных модулей для вариационного проектирования с существующими коммерческими геометрическими ядрами. Место вариационного геометрического решателя и других вычислительных модулей в архитектурной схеме современных САПР иллюстрируется на рисунке 1.

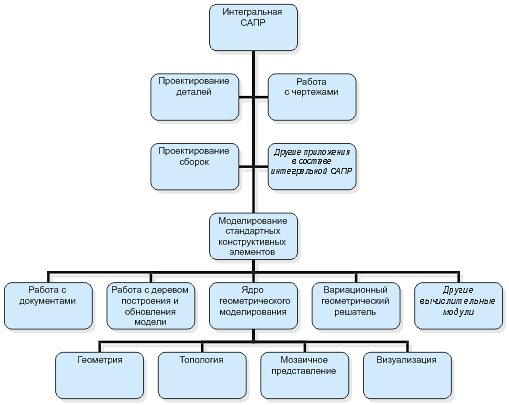
Рисунок 1. Архитектурная схема организации взаимодействия модулей интегральной САПР

Таким образом, в руки разработчику приложений САПР попадает исчерпывающий набор инструментальных библиотек (геометрическое моделирование + вариационное проектирование), которые сведут его задачу к сборке готового приложения из набора стандартных элементов. В таблице 2 перечислены некоторые из таких инструментальных наборов (toolkits), планируемые к выпуску силами компании ЛЕДАС, а в оставшейся части статьи мы кратко опишем базовую функциональность каждого из них.

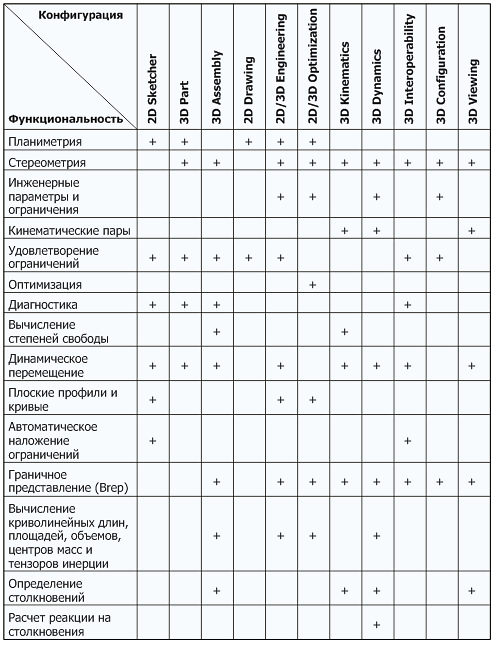
Таблица 2. Конфигурации основных прикладных пакетов на основе решателя LGS

Каждый такой инструментальный набор включает в себя специально сконфигурированную версию вариационного геометрического решателя LGS, дополненную набором взаимосвязанных вычислительных модулей, средствами их быстрой интеграции с любым ядром геометрического моделирования, а также детальное руководство для программиста, описывающее особенности создания конкретного приложения на основе данного инструментального набора. Для большинства наборов планируется также открыть код демонстрационного приложения с ограниченной функциональностью, созданного на основе ядра с открытым кодом Open CASCADE.

Редактор двумерных эскизов

В традиционных параметрических системах (на основе истории построения) форма профиля контролируется с помощью изменения параметров его элементов (вершин и дуг). Вариационное эскизное черчение выгодно отличается от этого подхода тем, что в любой момент конструктор может добавить или удалить любое логическое (инцидентность, параллельность, касание) или параметрическое (радиус дуги, длина отрезка, расстояние) ограничение между геометрическими элементами контура. В этом случае форма профиля автоматически изменяется системой (путем подбора новых значений параметров для элементов профиля), чтобы удовлетворить всем наложенным ограничениям (см. рис. 2). Дополнительным преимуществом вариационного подхода к созданию эскизов является возможность провести диагностику элементов эскиза (с тем, чтобы определить лишние или несовместные ограничения, а также выявить оставшиеся степени свободы). Кроме того, у пользователя имеется инструмент для динамического перемещения (с помощью манипулятора «мышь») геометрических элементов профиля по таким траекториям, на которых не нарушаются все заданные ограничения. Важной вспомогательной функциональностью приложений для эскизного черчения является автоматическое наложение ограничений на элементы, которое позволяет снять все оставшиеся степени свободы – с тем, чтобы полностью контролировать форму профиля путем изменения параметров ограничений.

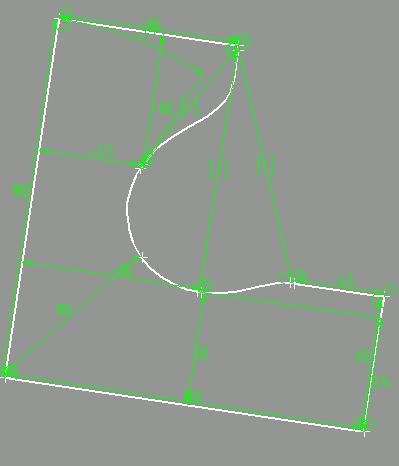
Рисунок 2. Использование вариационного подхода при проектировании криволинейного профиля

Геометрический решатель LGS 2D позволяет смоделировать все сущности, необходимые для реализации модуля вариационного черчения в САПР, в терминах планиметрических объектов – точек, бесконечных прямых, окружностей, эллипсов и произвольных кривых. При этом типичные элементы профиля, такие как отрезки и дуги, моделируются несколькими объектами LGS (например, отрезок моделируется заданием бесконечной прямой и пары точек на ней, дуга – окружностью с парой точек). Чтобы облегчить работу по встраиванию решателя LGS 2D в приложения для эскизного черчения, разработана специальная интеграционная технология, позволяющая на 90% автоматически обмениваться информацией с популярными коммерческими ядрами геометрического моделирования и организовывать передачу данных между элементами эскиза и их образами в LGS 2D. Технология включает в себя настраиваемый шаблон с кодом интеграционного модуля и детальное описание работы по его использованию с конкретным геометрическим ядром. Версия LGS 2D для эскизного черчения реализует следующие базовые функции: расчет новых координат объектов в соответствии с заданными между ними ограничениями, диагностика объектов и ограничений, динамическое перемещение объектов в соответствии с оставшимися степенями свободы, автоматическое наложение ограничений для удаления оставшихся степеней свободы. Дополнительный модуль в составе специального инструментального набора для реализации эскизного черчения позволяют рассчитывать текущие параметры ограничений и выбирать оптимальное место для их изображения на эскизе. Другой модуль моделирует такие сущности, как кусочно-гладкий профиль, кривая смещения (offset) и кривая соединения (connect), что облегчает задачу пользователя по поддержке таких сущностей в приложении. Существующая демонстрационная реализация модуля вариационного эскизного черчения (с ограниченным набором геометрических примитивов) на основе ядра геометрического моделирования Open CASCADE позволяет в полной мере оценить функциональность, производительность и удобство работы с соответствующим приложением, построенным на основе LGS 2D. Подробно документированный исходный код этого модуля (на языке С++) позволяет понять, как устроено это приложение с точки зрения программиста, а также использовать этот код для создания аналогичных приложений. Набор этих инструментов (специализированная версия LGS 2D, модули для интеграции с геометрическим ядром, размещения изображений ограничений на чертеже, работы с профилями, конечно-пользовательское демо-приложение для вариационного эскизного черчения с открытым кодом) вместе с обширным набором технической документации формируют LGS 2D Sketcher Toolkit, набор средств для быстрого создания приложения для вариационного эскизного черчения.

Проектирование трехмерных деталей, поверхностей и каркасов

При проектировании каркасов пользователь имеет дело с обстановкой, аналогичной редактору эскизов, только профили он создает не в двумерном, а в трехмерном пространстве. Вариационный подход дает здесь ровно те же преимущества, что и в двумерном случае – пользователь абсолютно не должен заботиться об истории построения, и волен накладывать на элементы каркаса столько ограничений, сколько ему необходимо.

Поверхности в трехмерном пространстве конструируются тремя основными способами. Фрагменты канонических поверхностей (сфер, цилиндров, конусов) задаются указанием декартовых координат этих поверхностей и пределов параметрического лоскута. Другие поверхности создаются на основе плоских и трехмерных профилей – путем их протягивания или вращения (причем, сам профиль может изменяться во время протягивания – соответствующая поверхность называется adaptive swept surface в англоязычной терминологии), либо путем внутренней аппроксимации замкнутого граничного профиля (fill). Наконец, поверхности третьего вида строятся на основе уже построенных поверхностей – это либо равноудаленные поверхности (offset), поверхности с переменным удалением от существующей (variable offset), а также поверхности, соединяющие (с требуемой степенью гладкости) другие поверхности (blended surface). Развитые средства проектирования поверхностей содержат также большое количество других инструментов. Вариационный решатель в данном контексте может использоваться как для управления изменяемым профилем при построении поверхности типа adaptive swept, так и для позиционирования поверхностей по отношению друг к другу (например, две поверхности можно расположить на заданном расстоянии друг от друга). Пользуясь преимуществами вариационного подхода, пользователь может наложить любые ограничения между поверхностями, кривыми и точками.

Для построения объемных элементов чаще всего используются такие конструктивные элементы, как вытянутые, повернутые или построенные по сечениям (плоским замкнутым профилям) основания и вырезы (pad, shaft, rib, pocket, groove и slot в английской инженерной терминологии). Другая группа конструктивных элементов основана на модификации уже построенных топологических элементов трехмерной модели – скругление (fillet), фаска (chamfer), наклон (draft) и др. Третья важная группа – это конструктивные элементы, построенные на основе криволинейных поверхностей – разрез (split), утолщение (thick), замыкание (close). Наконец, последнюю важную группу образуют элементы, построенные на основе других с помощью трансформаций (смещения, вращения, отражения). Вариационный подход позволяет связать параметры этих элементов друг с другом произвольным образом – например, можно позиционировать в трехмерном пространстве оси двух цилиндрических отверстий под заданным углом друг другу или задать расстояние в 3D между центрами их образующих окружностей.

Обычно при историческом подходе к построению объемных трехмерных моделей задание пространственных ограничений между элементами не допускается (можно измерить расстояние или угол между произвольными топологическими элементами, но нельзя изменить его значение), т.е. редактировать можно только параметры самих элементов. Дело в том, что моделирование объемной формы основано на истории построения конструктивных элементов – каждый из них строится по очереди. Однако, у пользователя современных систем есть возможность отказаться от истории построения элементов (создав так называемый базовый элемент – datum feature). Такие элементы перестают зависеть от других, поэтому их можно связать с другими элементами трехмерными ограничениями (как логическими, так и параметрическими), используя все основные преимущества вариационного подхода – точно как при работе с каркасами и поверхностями.

LGS 3D Part Toolkit содержит прежде всего базовую версию решателя LGS 3D, позволяющего связывать геометрическими ограничениями базовые объекты стереометрии: точки, бесконечные прямые и плоскости, окружности, цилиндры, сферы, конусы и т.п. Для удобства создания приложения на основе LGS 3D данный инструментальный набор содержит модуль, облегчающий интеграцию LGS 3D с популярными коммерческими ядрами для геометрического моделирования.

Проектирование сборок

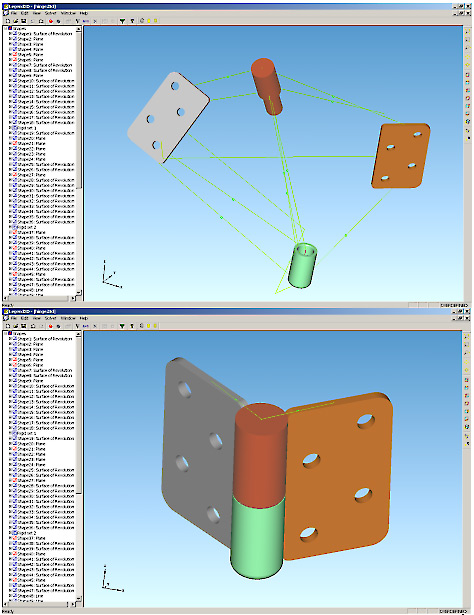
Рисунок 3. Сборка изделия методом «снизу вверх» с использованием вариационного подхода

Основной функциональностью приложения для проектирования сборок является возможность обновления сборки (update) – т.е. автоматическое удовлетворение всех наложенных пользователем ограничений путем перемещения деталей в пространстве (см. рис. 3). В процессе работы с одной сборкой пользователь может вызывать обновление несколько раз – при добавлении новых ограничений или при редактировании параметров ранее созданных.

В рамках вариационного подхода у пользователя имеется возможность наложить произвольное количество ограничений, что может привести к переопределенной или несовместной сборке. Переопределенная сборка содержит больше ограничений, чем требуется для взаимного расположения деталей в пространстве. Несовместная сборка содержит параметрические ограничения, текущие значения которых невозможно удовлетворить. Развитое приложение для проектирования сборок укажет пользователю на лишние и несовместные ограничения.

Типовой функциональностью приложения для проектирования сборок является возможность автоматически «разобрать» собранную сборку для того, чтобы увидеть каждую деталь отдельно.

Другой типичной функциональностью является проверка деталей в сборке на отсутствие пересечений их объемов (в т.ч. с заданным допуском). К этой же области относится вычисление и визуализация минимального расстояния в пространстве между двумя деталями в сборке.

Каждая деталь в сборке имеет от 0 до 6 степеней свободы (в зависимости от того, является ли она зафиксированной и какими ограничениями связана с другими деталями). Анализ и визуализация степеней свободы – важная функциональность приложения для проектирования сборок.

Другой важной функциональностью приложений для проектирования сборок является возможность динамического перемещения деталей в сборке, сохраняя удовлетворенными все наложенные ограничения. Траекторию перемещения задает пользователь, а приложение в интерактивном режиме пытается следовать этой траектории (с минимальными отклонениями), сохраняя все наложенные ограничения удовлетворенными. В случае, когда это невозможно, перемещение детали прекращается. Дополнительной особенностью развитых приложения для проектирования сборок является возможность проверки на столкновения деталей в процессе их динамического перемещения.

Создание трехмерных аннотаций и сечений, как правило, не требует использования вариационного подхода, т.к. аннотации и сечения однозначно позиционируются относительно референсного геометрического элемента, однако возможность связывания аннотаций и сечений геометрическими ограничениями представляется полезной. Наконец, многие приложения для проектирования сборок умеют вычислять механические характеристики деталей и всей сборки: объем, массу, площадь поверхности, центр масс и тензор инерции, а также поддерживают работу с ведомостью материалов (Bill of Materials, BOM).

В рамках инструментального набора LGS 3D Assembly Toolkit разработчикам будут доступны модули, реализующие большинство вышеперечисленных функций.

Работа с чертежами

Планируемый к разработке LGS 2D Drafting Toolkit позволит реализовать связь между трехмерной вариационной моделью и ее двумерными образами.

Инженерные знания

Геометрический решатель LGS позволяет работать не только с чистыми геометрическими задачами, но и со смешанными инженерно-геометрическими. В таких задачах пользователь может создавать свободные переменные, ассоциировать с некоторыми из них геометрические измерения между геометрическими элементами модели (расстояние, угол, радиус) и связывать переменные посредством инженерных ограничений – уравнений, неравенств, табличных зависимостей, а также с использованием внешних для решателя функций. Такой подход позволяет в рамках одного решателя эффективно обрабатывать смешанные инженерно-геометрические спецификации, применяя к ним символьные методы и более точные численные алгоритмы.

Дополнительным преимуществом может являться способность решателя напрямую вычислять длину криволинейного контура, площадь замкнутого двумерного контура, площадь ограниченной трехмерной поверхности, объем и центр масс тела. Соответствующие величины могут рассматриваться как переменные смешанной инженерно-геометрической модели, допуская тем самым различные интерактивные сценарии, невозможные в традиционной параметрической обстановке. Например, пользователь получает возможность интерактивного редактирования двумерного контура (путем динамического перемещения составляющих его элементов), сохраняя неизменной его площадь. Интерактивность такого сценария обеспечивается за счет применения эффективных алгоритмов к алгебраической постановке задачи, которая в данном случае полностью доступна решателю.

LGS 2D/3D Engineering Toolkit будет включать в себя специальную версию базового решателя LGS 2D/3D, расширенную возможностями спецификации инженерных ограничений (уравнений, неравенств и таблиц). Кроме того, интерфейсный модуль для работы с плоскими профилями (2D) или BRep представлением (3D) будет расширен возможностями расчета основных геометрических измерений – длины и площади контура, площади поверхности, объема и центра масс тела.

Параметрическая оптимизация

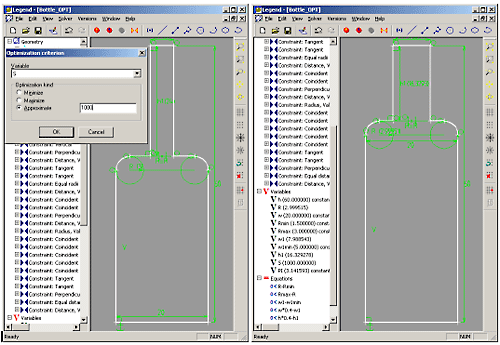
Рисунок 4. Оптимизация площади замкнутого контура с помощью LGS

Решатель LGS имеет возможности оптимизировать любой параметр в рамках смешанной модели – состоящей как из геометрических, так и из инженерных спецификаций (включая уравнения, неравенства, таблицы, измерения площадей и объемов, а также произвольные пользовательские функции, см. рис. 4). LGS 2D/3D Optimization Toolkit представляет собой расширение описанного ранее Engineering Toolkit возможностью задания целевого параметра и выбора алгоритма оптимизации.

Моделирование кинематики механизмов

Основные действия пользователя при проектировании механизмов можно разбить на три группы – сборка механизма (обновление), перемещение звеньев механизма и имитация движения механизма. Сборка и перемещение звеньев полностью аналогичны соответствующим операциям, решаемым при проектировании сборок. Имитация движения механизма состоит в том, что пользователь задает закон движения одного ведущего звена, а приложение автоматически рассчитывает и визуализирует движения всех звеньев механизма в соответствии с заданными кинематическими парами.

Более сложные действия пользователя включают в себя анализ механизма (подсчет степеней свободы звеньев, измерение скоростей и ускорений отдельных звеньев, визуализация траекторий движения точки, вычисление минимального расстояния между звеньями, определение столкновений и вычисление объема, заметаемого при движении звеньев) – многие из этих задач решаются также и в рамках приложений по проектированию сборок.

Несмотря на то, что анализ кинематики механизмов имеет много общего с проектированием сборок, вариационный решатель, лежащий в его основе, должен поддерживать расширенную функциональность. Речь идет, прежде всего, о возможности задания кинематических пар, не все из которых могут быть выражены через ограничения сборки. Однако возможность использования переменных геометрических измерений (существующая в решателе LGS) позволяет также задать передающие коэффициенты и условия на качение для криволинейных пар. Эта же особенность решателя используется и для спецификации закона управления механизмом, который может быть выражен в виде произвольной функции, задающей изменение угла или смещения кинематической пары во времени.

Находящийся в разработке LGS 3D Kinematics Toolkit включает в себя специальную версию LGS 3D с возможностью спецификации простых инженерных уравнений, а также модуль более высокого уровня, предоставляющий разработчику приложения проблемно-ориентированный интерфейс для спецификации кинематических пар и задания законов их движения.

Моделирование динамических взаимодействий

При использовании вариационного подхода с явно заданными ограничениями сборки (кинематическими парами) число степеней свободы в моделируемой системе существенно снижается, что позволяет описать ее более компактно в алгебраическом смысле и применить к такой поставке принцип Гамильтона, тем самым сведя задачу к дифференциальным уравнениям Лагранжа (в общем случае – дифференциально-алгебраическим уравнениям). Специальная версия решателя LGS 3D позволит эффективно решать такого рода системы, а в комбинации с модулем определения столкновений и модулем пересчета скоростей при столкновении составит основу пакета LGS 3D Dynamics Toolkit, в который также войдет модуль расчета объемов, центров масс и тензоров инерции тел на основе граничного (BRep) представления геометрии.

Параметризация геометрии при обмене данными между САПР

Планируемый к разработке LGS 3D Interoperability Toolkit будет включать в себя подмножество функциональности базового решателя LGS 3D, а также три дополнительных модуля. Интерфейсный модуль позволит накладывать геометрические ограничения непосредственно между элементами граничного представления геометрической модели (BRep) и создавать модель для LGS 3D, а модуль для автоматического распознавания логических ограничений геометрической модели позволит автоматически распознать соосности, касания, параллельности и перпендикулярности между гранями и ребрами. Наконец, интерфейсный модуль облегчит интеграцию данных инструментальных модулей с популярными геометрическими ядрами.

Проектирование изделия из стандартных комплектующих

Пакет LGS 3D Configuration Toolkit будет содержать функциональность, необходимую для поддержки работы с параметрическими каталогами деталей и быстрого проектирования сборных конструкций.

Средства для просмотра 3D моделей

Специальная «легкая» версия вариационного решателя войдет в состав LGS 3D Viewing Toolkit, набора инструментальных модулей для создания приложения по визуализации трехмерных моделей с внутренними степенями свободы.

За пределами традиционных средств механического проектирования

Образование – одна из самых перспективных областей приложений. На основе геометрического решателя LGS 2D было создано приложение FlashLGS, которое можно запускать в окне Интернет-браузера (см. рис. 5). Данное приложение позволяет моделировать базовые геометрические объекты (точки, отрезки, окружности) и связывать их логическими и параметрическими ограничениями. Интуитивно понятный пользовательский интерфейс, ограниченный набор примитивов и возможность запускать приложения прямо из окна браузера позволяют овладеть основами вариационного подхода к параметрическому черчению любому человеку даже без соответствующей подготовки. Кроме того, данное или подобное ему приложение может быть использовано в школах на уроках планиметрии для создания интерактивных иллюстраций к теоремам и задачам.

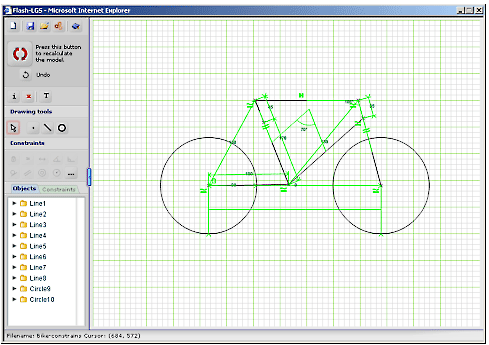
Рисунок 5. Вариационное эскизное черчение в окне Интернет-браузера (FlashLGS)

CAD 4D – популярная концепция в архитектурно-строительных САПР, позволяющая планировать изменения трехмерных моделей зданий во времени, т.е. планировать сам процесс строительства. В рамках данной концепции план-график строительства ассоциируется с трехмерными ресурсами. При этом ограничения сборки могут быть связаны с ресурсными ограничениями – обе эти разновидности ограничений успешно моделируются и решаются в рамках вариационного подхода, облегчая задачу пользователя по проектированию процесса строительства. В данном случае решатель LGS 3D может использоваться в связке с модулем Scheduler, разработанным в компании ЛЕДАС для решения оптимизационных задач ресурсно-календарного планирования.

Компьютерное зрение – важная прикладная область, в рамках которой приходится решать задачу построения трехмерной модели по ее двумерным образам. Вариационный геометрический решатель позволяет улучшить качество такого распознавания за счет возможности наложения ассоциативных ограничений, связывающих трехмерное тело с набором его проекций.

Вычислительная молекулярная биология решает задачи по моделированию взаимодействия макромолекул и имеет важные приложения в таких областях как медицина, сельское хозяйство, нанотехнологии. Описание макромолекулы на уровне составляющих ее частей сводится к заданию расстояний между точками в пространстве. Например, важный прикладной аспект имеет задача предсказания пространственной структуры белка по его линейной структуре (последовательности нуклеотидов), используя базу данных простых белков, пространственная структура которых уже известна. Данная задача решается путем нахождения похожих фрагментов в линейной структуре моделируемого белка и сопоставления им трехмерных моделей. Окончательная трехмерная структура в данном случае представляет собой комбинацию таких моделей, т.е. удовлетворение максимально возможного числа заданных ограничений расстояния между точками (фрагментами макромолекул). Вариационный решатель LGS 3D позволяет эффективно решать такие задачи, включающие десятки тысяч ограничений.

Об авторе

Директор по технологиям компании ЛЕДАС, Дмитрий Ушаков в 1995 году получил диплом магистра математики Новосибирского государственного университета, а в 1998 стал кандидатом физико-математических наук по специальности «Математическое обеспечение вычислительных машин, комплексов и компьютерных сетей». В 1993-1999 годах Д.Ушаков являлся научным сотрудником Российского НИИ искусственного интеллекта, став основным разработчиком универсального объектно-ориентированного расширяемого решателя задач удовлетворения и оптимизации в ограничениях. В рамках своей деятельности в компании ЛЕДАС Д.Ушаков занимался разработкой вычислительных программных компонентов для системы CATIA V5, на основе которых создан ряд приложений, последовательно применяющих вариационный подход к параметризации. Д.Ушаков является автором около пятидесяти научных работ.

О компании ЛЕДАС

ЗАО "ЛЕДАС" — независимая софтверная компания, образованная в Новосибирском Научном Центре (Академгородке) Сибирского отделения Российской Академии Наук в 1999 г. Являясь лидером в области вычислительных технологий, основанных на аппарате математических ограничений, ЛЕДАС хорошо известен как поставщик вычислительных программных компонентов для систем PLM (управления жизненным циклом изделия) и ERP (планирования ресурсов предприятия). В портфеле предложений компании – решатель геометрических ограничений для САПР (CAD/CAM/CAE), оптимизирующий процессор для систем управления проектами, планирования рабочей силы и организации собраний, интервальные технологии для организации баз знаний и совместного проектирования в САПР. Компания также оказывает своим заказчикам различные услуги в области PLM и ERP: разработка ПО, консалтинг, распространение продуктов партнеров, тренинги персонала.