В уходящем году инженерная отрасль отметила знаменательный юбилей – тридцать лет промышленного использования неоднородных рациональных B-сплайнов (сокращенно NURBS – от англ. Non-Uniform Rational B-Spline) для моделирования трехмерных кривых и поверхностей. В августе 1981 г. американский авиастроительный концерн Boeing предложил сделать NURBS частью промышленного стандарта IGES. И хотя это решение формально было утверждено только пару лет спустя, отрасль САПР среагировала на предложение моментально: в том же году о поддержке NURBS объявили обе ведущие компании, производящие инженерное ПО – SDRC и Computervision. Сейчас, 30 лет спустя, отыскать САПР без поддержки NURBS практически невозможно. В чем причина этого феномена? Почему изобретение NURBS революционизировало отрасль? Ниже мы попытаемся ответить на эти вопросы, а заодно вспомним всех исследователей, внесших вклад в развитие и становление NURBS.
Скульптурные поверхности
Хорошо известно, что научные исследования в области трехмерного геометрического моделирования начались вовсе не в рамках CAD (проектирования с помощью компьютера), а со стороны CAM (производства с помощью компьютера). Изобретение в начале 1950-х гг. станка с ЧПУ (числовым программным управлением) в MIT (Массачусетском технологическом институте, США) породило потребность в цифровой модели детали, необходимой для создания управляющей программы для станка. Изучением принципов моделирования трехмерных объектов занялись различные исследовательские группы, а основными заказчиками этих исследований стали крупнейшие предприятия аэрокосмической и автомобильной отраслей промышленности.

Рис. 1. Citroёn DS
Посмотрите на фотографию модели Citroёn DS (годы выпуска 1955-1975), ставшей автомобильной иконой на все времена. Точное изготовление таких сложных «скульптурных» поверхностей требует использования продвинутого математического аппарата, и совершенно не случайно одно из первых исследований в этой области было проведено французским математиком Полем де Кастельжо (Paul de Casteljau), работавшим на Citroёn. Он предложил способ построения гладкой поверхности по набору контрольных точек, задающих ее геометрические свойства. Результаты его работы были опубликованы только в 1974 г., но само исследование было проведено еще в 1959 г., что дает основания именно его считать автором кривых и поверхностей, получивших имя совсем другого француза – Пьера Безье (Pierre Bézier). Впрочем, прежде чем рассказать о нем, напомним о самой проблематике «скульптурных» инженерных поверхностей.
Как можно конструктивно (не в виде абстрактного алгебраического уравнения, а путем геометрических построений) задать гладкую поверхность, обладающую требуемой эстетической формой? Простейшим способом задания является указание четырех точек в трехмерном пространстве, которые формируют так называемый билинейный лоскут (bilinear patch):

Рис. 2. Билинейный лоскут
Билинейный лоскут является разновидностью линейчатой поверхности (ruled surface), которая целиком состоит из отрезков, соединяющих две кривых:
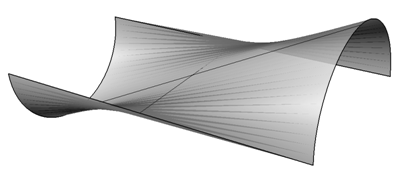
Рис. 3. Линейчатая поверхность
Стивен Кунс (Steven Coons), профессор MIT, обобщил такой способ задания на поверхности с двойной кривизной, получившие его имя (Coons patch):
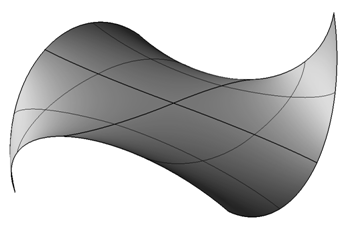
Рис. 4. Лоскут Кунса
Опубликованный им в 1967 г. препринт “Surfaces for Computer-Aided Design in Space Form” [Coons 1967] получил широкую известность как «Малая красная книга». Предложенный им аппарат граничных кривых и функций сопряжения дал основу для всех дальнейших исследований в этой области. Именно Кунс первым из исследователей предложил использовать рациональные полиномы для моделирования конических сечений. Выдающийся вклад Кунса в развитие отрасли САПР подчеркивается еще и тем, что он являлся научным руководителем Айвэна Сазерлэнда (Ivan Sutherland), создателя знаменитой системы Sketchpad, ставшей прообразом нынешних САПР.
Кривые Безье
Лоскут Кунса позволял контролировать форму поверхности на ее границах, но не между ними. Необходимость контролировать форму внутри хорошо понимал Пьер Безье, разрабатывавший в начале 1960-х гг. систему UNISURF для проектирования поверхностей автомобилей Renault.
Рис. 5. Пьер Безье
Безье, как истинный представитель французской математической школы, хорошо знал труды Шарля Эрмита (французского математика XIX в.), в частности аппарат кубических кривых, названных в его честь. Эрмитова кривая (Hermite curve) является геометрическим способом задания кубической кривой: с помощью концевых точек и касательных векторов в них. Варьируя направления и величины этих векторов, можно контролировать форму Эрмитовой кривой:
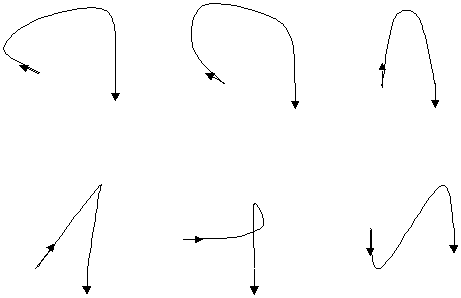
Рис. 6. Семейство Эрмитовых кривых
Безье не нравилось то, что, задавая Эрмитову кривую, мы указываем только ее поведение в концевых точках, но не можем влиять явным образом на форму кривой между этими точками (в частности, кривая может удалиться сколь угодно далеко от отрезка, соединяющего ее концевые точки). Поэтому он придумал конструктивно задаваемую кривую (позднее получившую его имя), форму которой можно контролировать в промежуточных, так называемых контрольных, точках. Кривая Безье (Bézier curve) всегда выходит из первой контрольной точки, касаясь первого отрезка ломанной, соединяющей все контрольные точки, и заканчивается в последней контрольной точке, касаясь последнего отрезка. При этом любая точка кривой всегда остается внутри выпуклого замыкания множества контрольных точек:
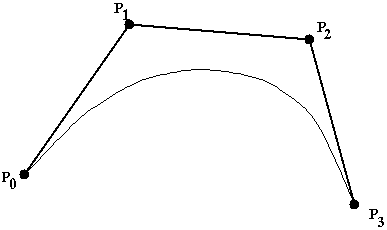
Рис. 7. Кривая Безье с четырьмя контрольными точками
Безье опубликовал работу по своим кривым в 1962 г., но когда двенадцать лет спустя компания Citroёn рассекретила свои исследования, выяснилось, что эти кривые были известны де Кастельжо как минимум за три года до Безье. Де Кастельжо описывал их конструктивно, и соответствующий алгоритм получил название в его честь.
Позднее Форрест установил связь между кривыми Безье и полиномами в форме Бернштейна (который были известны математикам еще с начала XX в.) Он показал, что функция, задающая кривую Безье, может быть представлена в виде линейной комбинации базисных полиномов Бернштейна. Это позволило исследовать свойства кривых Безье, опираясь на свойства данных полиномов.
Перейти от кривых к поверхностям Безье можно двумя способами. В первом вводятся так называемые образующие кривые Безье, имеющие одинаковую параметризацию. При каждом значении параметра по точкам на этих кривых в свою очередь строится кривая Безье. Перемещаясь по образующим кривым, получаем поверхность, которая называется поверхностью Безье на четырёхугольнике. Областью задания параметров такой поверхности является прямоугольник. Другой подход использует естественное обобщение полиномов Бернштейна на случай двух переменных. Поверхность, которая задается таким полиномом, называется поверхностью Безье на треугольнике.
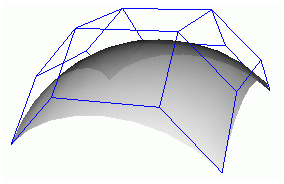
Рис. 8. Поверхность Безье
Сплайны
Кривые и поверхности Безье, являясь безупречным геометрическим конструктивом, имеют, однако, пару свойств, существенно ограничивающих их область применения. Одно из этих свойств состоит в том, что с помощью кривых Безье нельзя точно представить конические сечения (например, дугу окружности). Второй – их алгебраическая степень растет вместе с числом контрольных точек, что весьма затрудняет численные расчеты.
Способ борьбы с алгебраической степенью сложной кривой известен математикам давно – достаточно построить кривую, состоящую из гладко сопряженных сегментов, каждый из которых имеет ограниченную алгебраическую степень. Такие кривые называются сплайнами, а в математический обиход их ввел американский математик румынского происхождения Исаак Шёнберг [Schoenberg 1946]. Его теоретические работы практическим образом (в контексте САПР) переосмыслил Карл де Бур, американский математик немецкого происхождения. Его работа “On calculating with B-Splines”, равно как и вышедшая в том же году (1972) статья Кокса “The numerical evaluation of B-Splines” установили связь между геометрической формой составной кривой и алгебраическим способом ее задания.
B-сплайны являются обобщением кривых и поверхностей Безье: они позволяют аналогичным образом задавать форму кривой с помощью контрольных точек, но алгебраическая степень B-сплайна от числа контрольных точек не зависит.
Уравнение B-сплайна имеет вид, аналогичный кривой Безье, но сопрягающие функции не являются многочленами Бернштейна, а определяются рекурсивным образом в зависимости от значения параметра. Область задания параметра B-сплайна разбита на узлы (knots), которые соответствуют точкам сопряжения алгебраических кривых заданной степени.
Изобретение NURBS
Первой работой с упоминанием NURBS стала диссертация Кена Версприла (Ken Versprille), аспиранта Сиракузского университета в Нью-Йорке [Versprille 1975].

Рис. 9. Кен Версприл, изобретатель NURBS
Версприлл получил степень бакалавра математики в Университете Нью-Хэмпшира, затем обучался в магистратуре и аспирантуре Сиракузского университета, где в то время работал профессором Стивен Кунс. Проникшись идеями Кунса, Версприл опубликовал первое описание NURBS и посвятил этой теме свою диссертацию. Вскоре после защиты он был принят на работу в компанию Computervision на должность старшего программиста для разработки функционала трехмерного моделирования в системе CADDS 3. И хотя порученная ему работа (реализация сплайнов) совпадала с интересующей его темой, его босс, будучи сконцентрирован на выполнении проекта в срок, настоял на отказе от NURBS и реализации более простого (с математической точки зрения) аппарата кривых Безье.
Спустя несколько лет Версприлл занял руководящую позицию в Computervision, и компания наконец решила поддержать NURBS. Программист, которому поручили реализацию, пришел к Кену за советом, который не заставил себя ждать: «Измени в таком-то файле такой-то флаг с 0 на 1 и перекомпилируй код!» Оказалось, что Версприлл с самого начала реализовал NURBS, просто не включил соответствующий код в релиз. И после исправления пары ошибок этот код заработал!
В 2005 году CAD Society, некоммерческая ассоциация отрасли САПР, присудила Кену Версприллу награду за неоценимый вклад в технологию САПР в виде NURBS. Премия была вручена на конгрессе COFES, состоявшемся в том же году в Аризоне.
Вклад Boeing
В 1979 г. авиастроительная корпорация Boeing решила начать работы по разработке собственной CAD/CAM системы под названием TIGER [Solid Modeling 2011]. Одна из задач, стоявших перед ее разработчиками, состояла в выборе подходящего представления для 11 требуемых форм кривых, включавших в себя все от отрезков и окружностей до кривых Безье и B-сплайнов. В процессе работы один из исследователей – Юджин Ли (Eugene Lee) – обнаружил, что основная задача (нахождение точки пересечения двух произвольных кривых) может быть сведена к решению задачи нахождения точки пересечения кривых Безье, поскольку любая гладкая кривая в некоторой окрестности может быть аппроксимирована кривой Безье. Это мотивировало исследователей к поиску способа представления всех кривых с использованием одной формы. (О диссертации Версприла они, похоже, ничего не знали.)
Важным локальным открытием стала возможность представления окружностей и других конических сечений с помощью рациональных кривых Безье [Lee 1981]. Другим шагом к открытию стало использование в промышленной практике давно известных из научной литературы неоднородных B-сплайнов. Наконец, исследователи пришли к интеграции двух этих понятий в единую формулу – NURBS. После чего потребовалось немало усилий, чтобы убедить всех остальных разработчиков TIGER начать использовать единое представление для всех типов кривых.
Вскоре после этого компания Boeing предложила включить NURBS в формат IGES, подготовив технический документ с исчерпывающим описанием нового универсального типа геометрических данных. Предложение было с энтузиазмом воспринято – прежде всего, благодаря позиции компании SDRC.
Вклад SDRC
В 1967 г. бывшие профессора машиностроительного факультета Университета Цинциннати (США) создали компанию SDRC (Structural Dynamics Research Corporation). Изначально ориентированная на оказание консалтинговых услуг в области машиностроения, SDRC со временем превратилась в одного из ведущих разработчиков САПР в мире. Начав с области CAE (средств инженерного анализа) компания затем сосредоточилась и на CAD (проектирование), разработав систему I-DEAS, которая позволяла решать широкий спектр задач – от концептуального проектирования посредством каркасного и твердотельного моделирования до черчения, конечно-элементного анализа и составления программ для станков с ЧПУ. В основе САПР I-DEAS лежала подсистема твердотельного моделирования GEOMOD.
Изначально GEOMOD представляла твердые тела в виде многоугольных сеток, аппроксимирующих их оболочку. Осознав важность предложения Boeing по стандартизации NURBS, программисты SDRC с энтузиазмом взялись за реализацию NURBS в GEOMOD. Основным разработчиком алгоритмов был Уэйн Тиллер (Wayne Tiller), впоследствии ставший соавтором знаменитой монографии "The NURBS Book" [Piegl 1997].

Рис. 10. Уэйн Тиллер, президент GeomWare, соавтор "Книги NURBS"
Система I-DEAS прекратила свое существование, после того как в 2001 г. компания EDS поглотила SDRC, а Уэйн Тиллер применил полученный опыт при реализации библиотеки NLib (см. ниже).
Вклад GeomWare, IntegrityWare и Solid Modeling Solutions
Американская компания IntegrityWare с 1996 г. разрабатывает набор библиотек для геометрических вычислений. В 1998 г. она заключила соглашение с компанией Solid Modeling Solutions о разработке ядра твердотельного моделирования SMLib, первая версия которого увидела свет в том же году.
Ядро SMLib устроено в виде «матрешки», где каждый уровень вложенности является отдельной библиотекой функций или классов. Самой вложенной «матрешкой» является библиотека функций NLib (NURBS Library), разработанная партнерской компанией GeomWare. NLib предоставляет исчерпывающий набор функций для конструирования и манипулирования кривыми и поверхностями NURBS. Алгоритмы NLib основаны на классической монографии [Piegl 1997], а один из ее авторов – Уэйн Тиллер является основателем и президентом компании GeomWare. Библиотеку NLib используют более 85 компаний, разрабатывающих инженерное ПО.
На основе NLib реализована объектно-ориентированная библиотека GSNlib (General Surface NURBS Library), предоставляющая набор методов для создания, редактирования, получения информации и пересечения кривых и поверхностей NURBS. Самой компанией IntegrityWare эта библиотека распространялась под именем GSLib и была лицензирована такими компаниями как Robert McNeel & Associates (для разработки Rhino 3D) и Ford Motor Company.
Поверхности подразделения
Поверхности подразделения (subdivision surfaces) представляют собой мозаичные (полигональные) модели, которые итеративно строятся по базовой сетке (base mesh), с каждой итерацией приближаясь к форме моделируемой поверхности. Таким образом, две составные части поверхности подразделения – это базовая сетка и алгоритм ее сглаживания. Исторически теория поверхностей подразделения началась с работы американского художника-дизайнера Чайкина (Chaikin), который предложил способ итеративного построения кривой по контрольным точкам. Аналогично Безье, построение кривой Чайкин начинает с характеристической ломанной, задаваемой набором контрольных точек. На следующем этапе образуется новая последовательность контрольных точек, которая строится по особым правилам на основе первой последовательности. Геометрически это похоже на обрезание углов (corner cutting) начальной ломаной – каждый ее отрезок делится в соотношении 1:2:1 и углы между двумя отрезками обрезаются за счет вставки новых отрезков между укороченными старыми. Процесс продолжается до тех пор, пока кривая не станет достаточно гладкой.
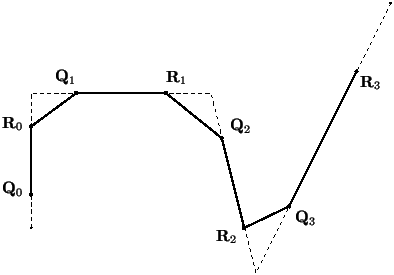
Рис. 11. Метод Чайкина
Вскоре после изобретения Чайкина было доказано, что генерируемая его алгоритмом кривая есть не что иное, как квадратичный однородный B-сплайн.
Метод Чайкина лег в основу целого семейства алгоритмов, предложенных его последователями. Одним из таких алгоритмов стал предложенный Ду (Doo) и Сабиным (Sabin) метод построения квадратичной однородной B-сплайновой поверхности по базовой четырехугольной сетке (каждая грань в такой сетке является выпуклым четырехугольником) [Doo 1978]. Вскоре они смогли распространить свой метод на любые базовые сетки, в которых каждая грань может иметь произвольное число вершин – 3, 4, 5… Полученная поверхность при этом локально (за исключением конечного числа точек) является квадратичным однородным B-сплайном. Метод Ду–Сабина состоит в том, что на очередном шаге каждая грань заменяется гранью меньшего размера с тем же количеством вершин. При этом каждая вершина уменьшенной грани есть среднее арифметическое исходной вершины, центров двух смежных ребер и центра самой грани. В результате получается несвязная сетка, в которой затем каждая новая вершина соединяется со всеми другими вершинами, полученными из одной и той же старой вершины, образуя новые грани. Полученный связный многогранник представляет собой основу для следующего шага алгоритма. Нетрудно видеть, что этот метод, как и метод Чайкина, состоит в обрезании углов:
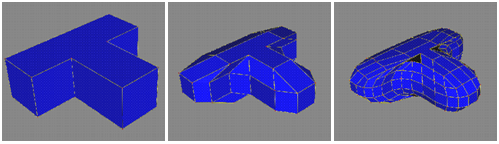
Рис. 12. Метод Ду-Сабина
Аспиранты университета Юты Кэтмал (Catmull) и Кларк (Clark) смогли расширить метод обрезания углов для построения однородных кубических B-сплайнов (каждый локальный участок поверхности подразделения Кэтмала-Кларка является B-сплайном - за исключением конечного числа точек) [Catmull 1978]. Предложенный ими метод, как и метод Ду–Сабина, может работать на базовых сетках произвольной топологии (получаемая поверхность является локально подобной кубическому B-сплайну). Алгоритм сглаживания состоит в итеративном построении новой сетки по несколько другим правилам. Работу метода иллюстрирует следующий рисунок:
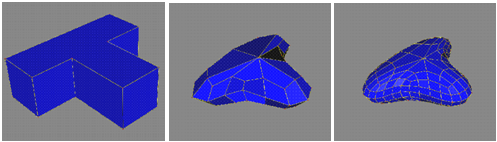
Рис. 13. Метод Кэтмала-Кларка
Поверхности подразделения – удобный способ представления гладких поверхностей компактным образом. Это свойство широко используется для представления различных объектов живой природы, а поэтому хорошо подходит также для описания сложных поверхностей в системах поверхностного моделирования. (Для поддержки негладких сопряжений – острых ребер – используются специальные атрибуты, которые ограничивают область действия алгоритмов подразделения.)
В настоящее время разрабатывается несколько промышленных стандартов обмена геометрическими данными на основе поверхностей подразделения.
Чем же хороши NURBS?
Почему же кривые и поверхности NURBS сыграли столь важную роль в развитии САПР? Прежде всего потому, что они предлагают общую математическую форму для представления как аналитических геометрических объектов, так и кривых и поверхностей свободной формы. Манипуляция контрольными точками и весами NURBS позволяет гибко проектировать большое разнообразие геометрических форм. Расчеты с NURBS выполняются достаточно быстро и являются численно устойчивыми. Кривые и поверхности NURBS имеют ясную геометрическую интерпретацию, которая особенно полезна для дизайнеров, имеющих хорошие знания геометрии. NURBS обладают богатым набором инструментов (вставка/удаление/изменение узла, повышение степени, расщепление), которые могут быть использованы при создании и анализе этих объектов. NURBS являются инвариантом операций масштабирования, вращения, трансляции, обрезания, построения параллельных и перспективных проекций [Piegl 1991].
В то же время представление кривых и поверхностей в виде NURBS имеет ряд недостатков. Прежде всего, возрастает расход памяти: например, представление окружности в виде NURBS-кривой требует задания семи контрольных точек и десяти узлов, для чего требуется хранить в памяти 38 чисел с плавающей точкой вместо семи (центр, нормаль, радиус). Неверное применение весов может привести к очень плохой параметризации, которая сделает невозможной дальнейшие построения на основе NURBS. Некоторые алгоритмы (такие как нахождение пересечения двух поверхностей) лучше работают с традиционной формой представления. Наконец, некоторые фундаментальные алгоритмы (такие как обратные отображения) являются численно неустойчивыми в случае NURBS.
Несмотря на все эти недостатки, NURBS продолжают широко применяться в САПР – ведь ничего лучшего придумано не было. Впрочем...
T-сплайны
T-сплайны - вид поверхности свободной формы, подобной неоднородному рациональному B-сплайну (NURBS). Ключевое отличие T-сплайнов от NURBS состоит в том, что контрольные точки NURBS-поверхности должны образовывать топологическое подобие прямоугольной решетки, в то время как у T-сплайнов допустимы так называемые внутренние T-точки (контрольная точка с тремя, а не четырьмя соседями).
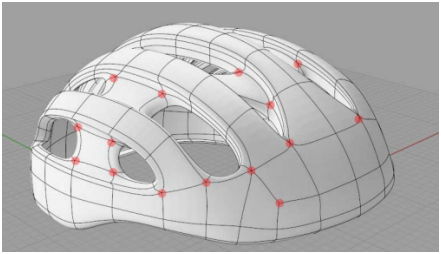
Рис. 14. Т-сплайн
При моделировании органических поверхностей с помощью T-сплайнов удается сократить число контрольных точек вдвое по сравнению с NURBS (при тех же требованиях к G2-гладкости поверхности).
T-сплайны были изобретены Томасом Седербергом (Thomas Sederberg) [Sederberg 2003]. В той же работе предложено понятие T-NURCCs, являющееся обощением Т-сплайнов и поверхностей подразделения Кэтмала-Кларка и представляющее собой единый математический аппарат для работы с NURBS, Т-сплайнами и поверхностями подразделения. Для промышленного применения этой технологии в 2004 г. была основана компания T-Splines, Inc. (США), разрабатывающая собственные конечно-пользовательские программные продукты и библиотеки для разработчиков.
Вытеснит ли эта запатентованная технология NURBS? Время покажет.
Постскриптум
В тот же день, когда была опубликована эта статья, пришло известие о поглощении технологических активов T-Splines компанией Autodesk. Этот шаг однозначно свидетельствует об отраслевом признании Т-сплайнов. Вскоре эта технология появится в продуктах Autodesk, а значит и другие поставщики не смогут остаться в стороне от нее. Ждем появления Т-сплайнов в STEP?Литература
Catmull, E., and Clark, J., 1978, Recursively generated B-spline surfaces on arbitrary topological meshes, Computer-Aided Design 10(6):350-355.
Coons S. А., 1967, Surfaces for Computer Aided Design of Space Form, MIT Project MAC, AUC-TR-41. http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TR-041.pdf
Cox, M. G., 1972, The Numerical Evaluation of B-Splines, J. Inst. Mathematics and Applications, Vol. 10, pp. 134-149.
De Boor, C., 1972, On Calculation with B-Splines, J. Approximation Theory, Vol. 6, No. 1, pp. 50-62.
Doo, D., 1978, A subdivision algorithm for smoothing down irregularly shaped polyhedrons, Proceedings on Interactive Techniques in Computer Aided Design, pp. 157-165.
Lee, E. T. Y., 1981, A Treatment of Conics in Parametric Rational Bezier Form, Boeing document, Boeing, Seattle, Wash.
Piegl, L., 1991, On NURBS: A Survey, IEEE CG&A, Vol. 11, No. 1, pp. 55-71. http://www.ece.uvic.ca/~bctill/papers/mocap/Piegl_1991.pdf
Piegl, L. A., and Tiller, W., 1997, The NURBS Book, Springer.
Schoenberg, I. J., 1946, Contributions to the problem of approximation of equidistant data by analytic functions, Part A: On the problem of smoothing or graduation, a first class of analytic approximation formulas, Quart. Appl. Math. 4, 45–99.
Sederberg, T.-W., Zheng, J., Bakenov, A., and Nasri, A., 2003, T-Splines and T-NURCCs, ACM Transactions on. Graphics, 22(3), 477-484, http://cagd.cs.byu.edu/~tspline/innovation/papers/tspline.pdf
Solid Modeling Solutions, 2011, NURBS at Boeing. http://www.smlib.com/white%20papers/nurbsatboeing.htm
Versprille, K. J., 1975, Computer-Aided Design Applications of the Rational B-Splines Approxamation Form, doctoral dissertation, Syracuse Univ., Syracuse, N.Y.


