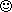У нас тут анти-анти-антиординаты.
Стоим на пятках твердо мы и на своем, —
Кто не на пятках, те…
Владимир Высоцкий. Марш антиподов
Введение
На рис. 1 показаны две группы овальных кривых. Это циклоп и эллипс со своими эквидистантами.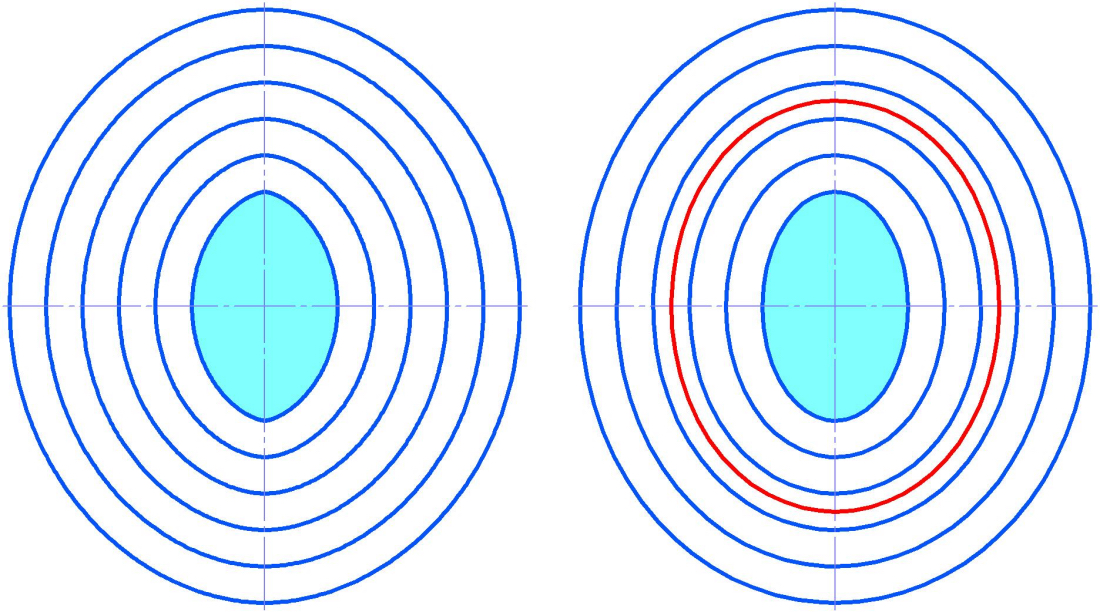
Рис. 1
Квазициклопы
Циклоп (циклоидальный овал) был изучен и описан в нескольких статьях, в том числе, относительно недавно и на страницах isicad (см. «Циклоп. Такой, какой есть» и «Второе рождение циклоидального овала, или как был разобран по косточкам циклоп».Что происходит с циклопом при его масштабировании по различным осям, мы уже знаем – получаются псевдоциклопы трёх типов.
А как будут выглядеть эквидистанты циклопа? Несколько таких эквидистант построены и показаны на рис. 1 (слева). На циклопа они уже похожи мало, однако, это всё те же овальные кривые, только со своей геометрией. Это и есть квазициклопы. Их площадные контрпрямоугольные коэффициенты (отношение площади овала к площади описанного прямоугольника) по мере удаления эквидистант от базовой кривой изменяются от 0,75 (соответствующая константа циклопа) до π⁄4 = 0,785398… (соответствующая константа окружности). Понятно, что по мере удаления от циклопа овалы приближаются по геометрии к окружности. Так что квазициклопы – это в некотором роде гибриды между циклопом и окружностью. Дадим определение этой фигуры.
Квазициклоп – эквидистанта циклопа, плоская, гладкая, замкнутая, переменной кривизны, симметричная относительно двух осей, четырёхполюсная, двухфокусная кривая. Имеет два апоцентра и два перицентра, совпадающих с полюсами большой оси. По контрэллипсной классификации квазициклопы – гипоовалы. Свойства характерных точек кривой аналогичны соответствующим свойствам циклопа (за исключением перицентров). Характерными точками максимумов суммы отрезков от точки на кривой до фокусов являются полюсы на большой оси, минимумы – в точках падения большого и малого фокальных лучей.
Эквиэллипсы
Эллипс – ещё тот овал! Никаких псевдоэллипсов он не позволяет из себя сделать. При масштабировании может менять форму, размеры, расположение фокусов, но при этом всегда остаётся эллипсом, не теряя своих уникальных свойств.Ну а как насчет эквидистант эллипса? И вот тут он сдаётся – благодаря ним получаем новые кривые – эквиэллипсы (рис. 1 справа). Почему не квазиэллипсы по примеру квазициклопов? Термин квазиэллипс в математике уже используется, поэтому «квази» заменено на «экви» (от эквидистанты). При увеличении параметра эквидистанты, овалы постепенно теряют очертания эллипса и приобретают форму, близкую к окружности.
Поскольку площадные контрпрямоугольные константы эллипса и окружности равны π⁄4, можно было предположить, что, соответствующие площадные коэффициенты эквиэллипсов также равны между собой и равны π⁄4. При проверке предположения выяснилось, что это не так. Вначале эти коэффициенты растут и, достигнув определённого максимального значения, начинают уменьшаться, опять до значения π⁄4, но в бесконечности.
Определения кривой давать не будем, скажем только о различиях с квазициклопом, дополнительно к сказанным выше: по контрэллипсной классификации эквиэллипсы являются двухфокусными гиперовалами; характерными точками максимумов суммы отрезков от кривой до фокусов являются точки падения большого и малого фокальных лучей.
Антиэллипсы
Эквиэллипс с максимальным площадным контрпрямоугольным коэффициентом предлагается назвать «антиэллипсом», поскольку он, из всех эквиэллипсов, наиболее сильно отличается по этому параметру от эллипса. На рис. 1 антиэллипс показан красным цветом. Антиэллипс – своеобразный антипод эллипса и существует не как необходимость, но как данность.Каждому конкретному (по форме и размерам) эллипсу соответствует множество эквиэллипсов и… только один антиэллипс (рис. 2). Это, пожалуй, главное свойство эквидистант эллипса и основное различие между квазициклопами и эквиэллипсами, поскольку циклопы антиподов не имеют.
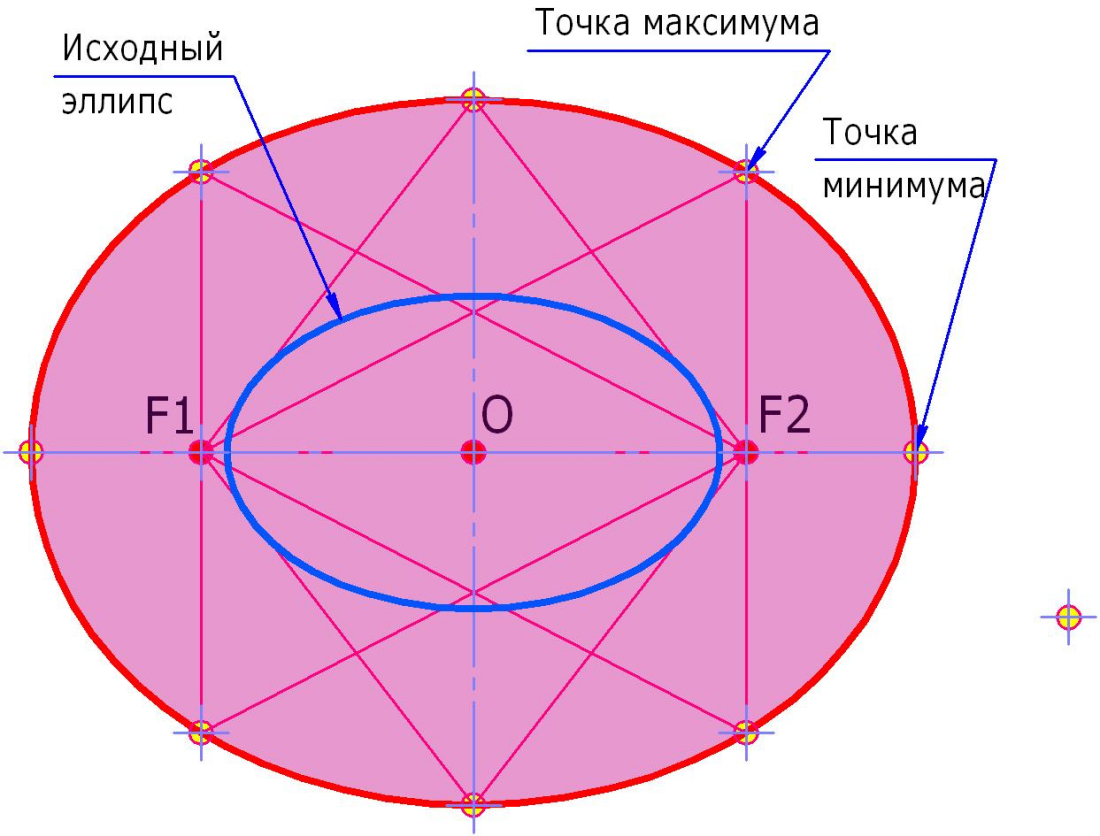
Рис 2
Ещё одно свойство антиэллипсов: по мере удлинения исходного эллипса растёт площадной контрпрямоугольный коэффициент соответствующего ему антиэллипса. Антиэллипсы отличаются друг от друга не только вышеуказанным коэффициентом, но и формой (рис. 3).
Рис. 3
Выводы
Оправдано ли присвоение имён этим кривым? Про антиэллипс уже сказано выше. Ну, а квазициклоп. Как бы пришлось назвать соответствующий ему овалоид вращения, не используя это имя: овалоид вращения эквидистанты циклопа. Не проще ли – квазициклопический (или квазициклоидальный) овалоид? То же и с эквиэллипсом.Преимущество описанных кривых – это простота построения. Имея базовые кривые эллипс и циклоп, при помощи эквидистант эти кривые могут быть получены моментально и никаких формул и расчётных модулей (это не касается антиэллипса, радиус эквидистанты которого необходимо определить).
Являются ли описанные выше кривые новыми? Пожалуй, это с уверенностью можно сказать только про квазициклопа (в полку циклопа и циклопоподобных прибыло!). А эллипс – «древняя» кривая, такая трансформация его проводилась и ранее, так что новизны в эквиэллипсе нет, разве только новое название. Но описывал ли кто-либо эти кривые, выделял ли кто-нибудь антиэллипс из ряда эквидистант эллипса? Мне это пока не известно. Если кто что-либо знает, просветите….
В одной из книг по геометрии я находил высказывание (вывод), что «внешняя эквидистанта эллипса, в отличие от внутренней, не имеет особенностей» и, как видим, оно справедливо только относительно внешнего вида кривой, но не всех её свойств.
По применению кривых: можно рекомендовать использовать их в архитектуре, дизайне.
Рис. 4
Рис. 5
Да, понять сложно, но когда понял именно ДА!!!
За 8 лет АСКОН стал зарабатывать в 6 раз больше ·
Обложка огонь
За 8 лет АСКОН стал зарабатывать в 6 раз больше ·
У Николенко есть ссылка на Аирбас, где есть ограничения на уровень технологии при проектировании.
Реализация MBSE-подхода при проектировании сложной продукции в PLM-решении АСКОН ·