
Вы, возможно, считаете, что свойства эллипсов и их геометрия полностью изучены?
Если честно, то и я не очень верил в существование каких-либо неизвестных свойств эллипса, поэтому долго не решался подступиться к нему, тем более, что он – один из самых «древних», известных и применяемых овалов. А если такие (неизвестные) свойства у него всё-таки есть, то чего им в неизвестности-то пребывать, пусть чтобы и о них знали. Короче, приступаем к проверке, есть ли они. 
На самом деле, вот, что побудило меня это делать: при изучении различных эллипсовидных овальных кривых выяснилось, что они могут иметь разное количество фокусов, которые в свою очередь могут обмениваться с противоположными фокусами разным количеством лучей. Так может быть и у эллипсов…?
Приведу примеры: эллипс – 2 фокуса, которые обмениваются бесчисленным множеством лучей; овал R-0 – нет фокусов; овал R-1 – 2 фокуса, которые могут обмениваться 8 парами отражённых лучей и парой прямых лучей; гипоэллипсы Ламе – 2 или 4 фокуса, каждая пара которых обменивается также 9 парами лучей.
Стоит особо сказать ещё о двух овальных кривых, это овал Кассини (в овальном диапазоне) и гиперэллипс Ламе, при проверке которых в каждом из них выявлено по два 9-лучевых и два 7-лучевых фокуса. Характерное отличие последних фокусов от 9-лучевых – 2 луча каждого фокуса являются лучами двойного отражения. На рис. 1 изображены эти кривые.
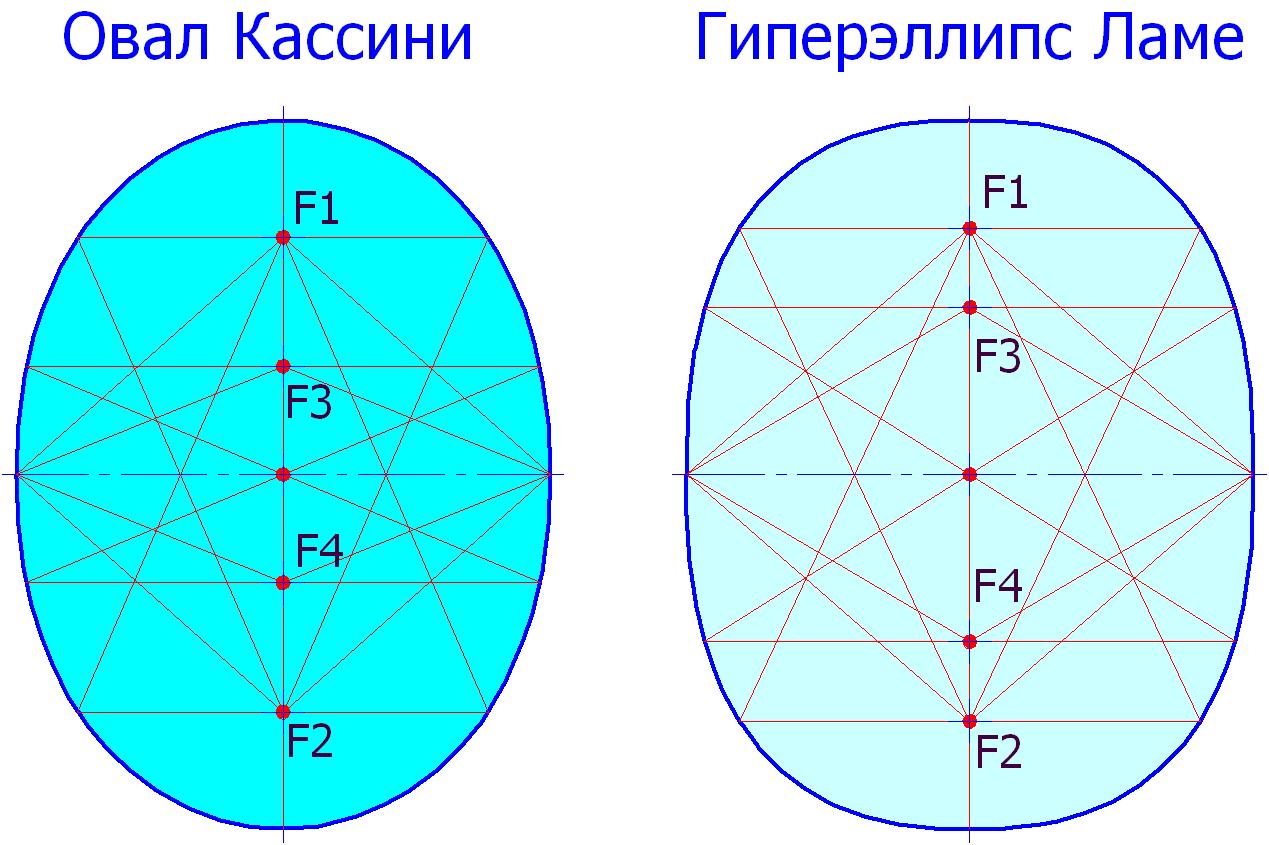
Рис. 1
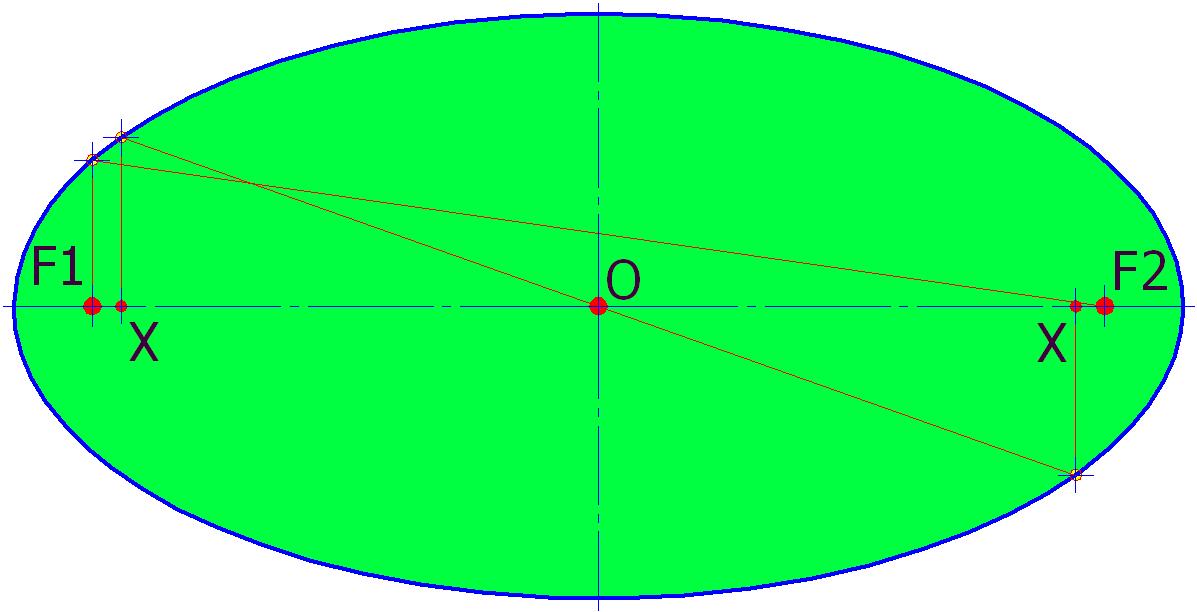
Рис. 2
Прежде, чем продолжить рассказ о точках X, или дополнительных фокусах эллипса, для упрощения терминов, введём следующую классификацию фокусов эллипсовидных овальных кривых: фокусы эллипсов – высшая категория; 9-лучевые фокусы – 1 категория и 7-лучевые – 2 категория.
Теперь зададимся вопросом: могут ли эллипсы помимо своих основных фокусов иметь фокусы 1 и 2 категорий? По фокусам 1 категории вопрос автоматически снимается, поскольку они полностью совпадают с основными фокусами.
А вот с фокусами 2 категории (на рис. 2 – это точки X) интересней и сложнее: как выяснилось при построении, эти фокусы есть у эллипсов, но не у всех!
Своеобразной «демаркационной линией», отделяющей одни от других, является число √2, это минимальное значение соотношения большой и малой осей эллипса, при котором и ниже которого фокусов 2 категории в эллипсе не будет. Квадратные корни любят вмешиваться в геометрию (вспомните антиэллипсы http://isicad.ru/ru/articles.php?article_num=18937).

На рис. 3 изображён один из четырёхфокусных эллипсов. Фокусы 2 категории F3 и F4 соединены между собой 7 парами лучей.
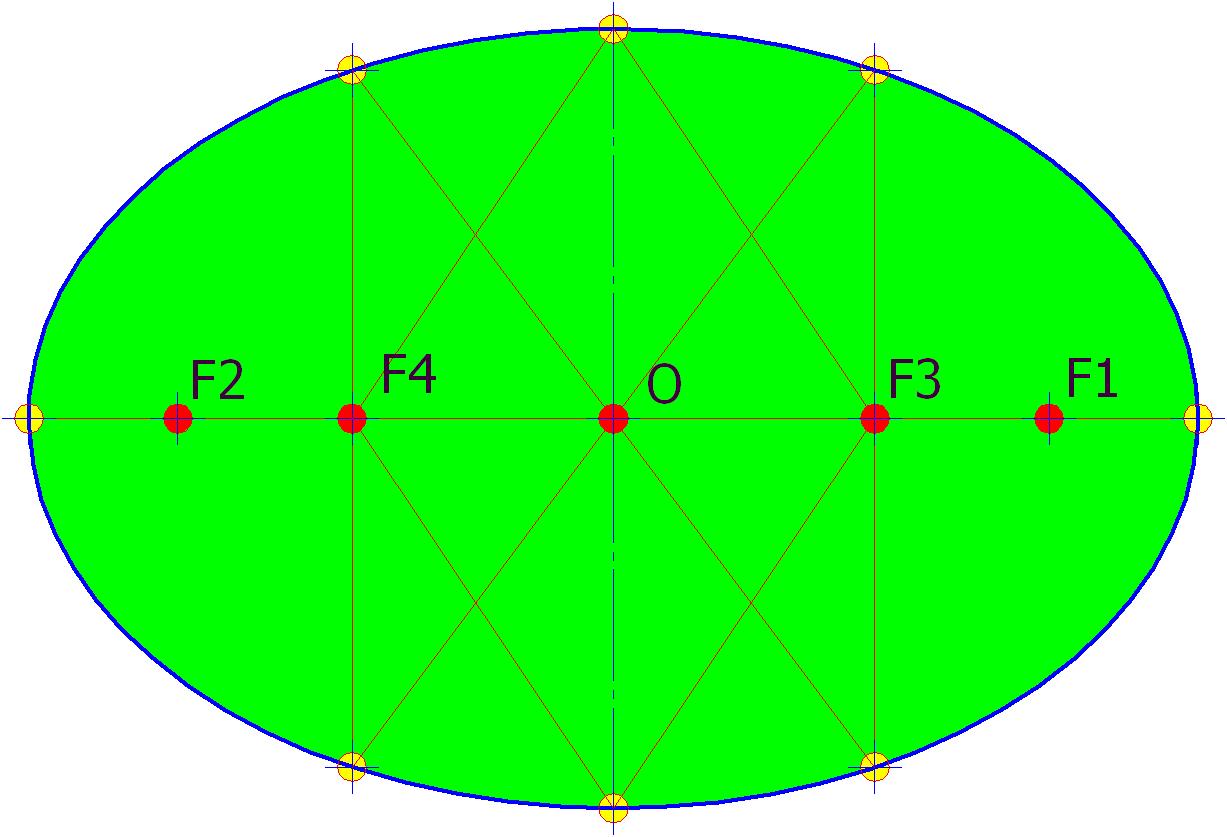
Рис. 3
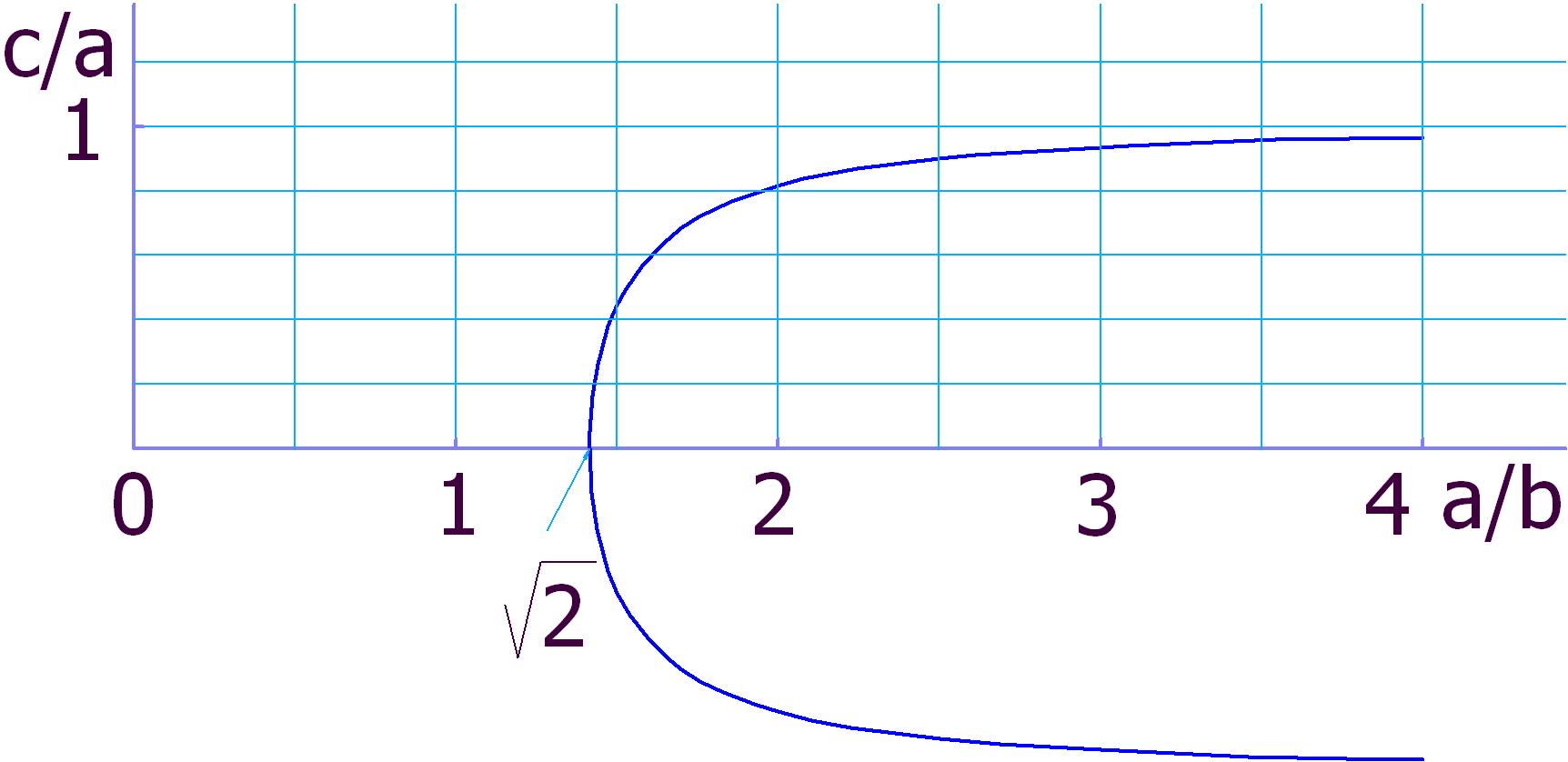
Рис. 4
Выводы:
- Подтверждено предположение о наличии дополнительных фокусов у ряда эллипсов. Четырёхфокусные эллипсы существуют!;
- Определено граничное значение соотношения осей эллипса, при котором появляются (исчезают) 7-лучевые фокусы (фокусы 2 категории);
- Построен график зависимости фокального расстояния фокусов 2 категории от соотношения осей эллипса.
Рис. 5

