Предлагаю читателям совместно решить одну геометрическую задачу, точнее, найти ответы на четыре её вопроса.
Предположим, что три мясокомбината (специализирующиеся на выпуске колбасных изделий), которые уже добились отменных вкусовых качеств своих колбас, решили привлечь дополнительных покупателей оригинальной формой их батонов. Думаю, что это реальная ситуация, поскольку многие видели (и не только), например, батоны сырокопчёной колбасы разнообразной формы.
И вот какие формы (срезы, нормальные к продольным осям батонов) они решили применить (рис. 1).
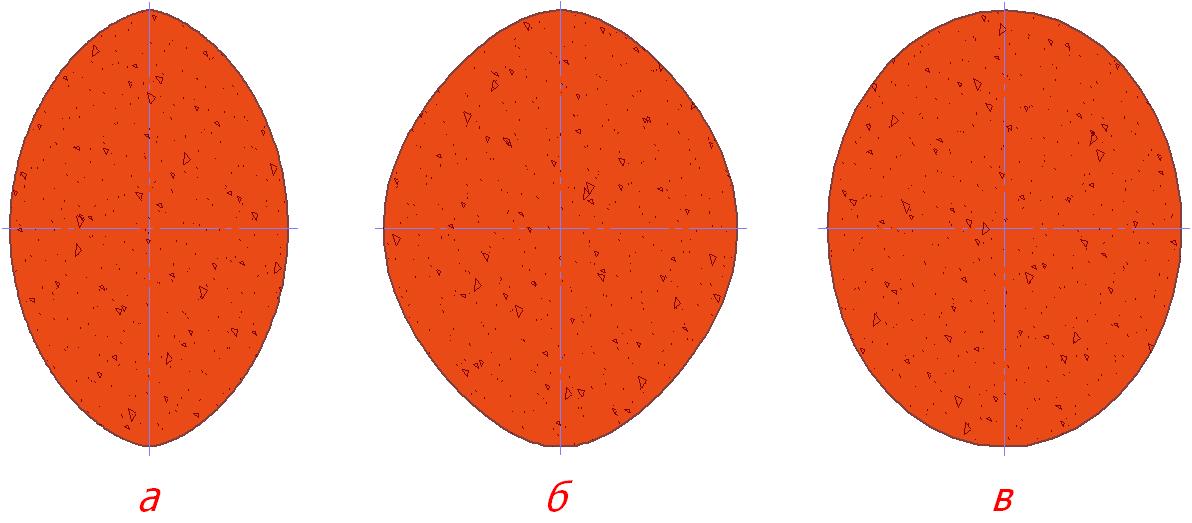
Рис. 1. Три овальные кривые
Вопрос 1
Назовите имена этих овалов.Вопрос 2
Назовите число элементов, необходимое и достаточное для построения каждого из этих овалов.Вопрос 3
Какие по форме срезы будут получены при сечении этих батонов одной и той же плоскостью общего положения (не перпендикулярной ни одной плоскости проекций): симметричные относительно двух осей, симметричные относительно одной оси или симметричные только относительно центра?Вопрос 4
Какими плоскостями необходимо рассечь эти батоны, чтобы получить сечения, вдвое превышающие по площади срезы, нормальные к продольной оси? Другими словами, назовите углы между плоскостями этих сечений и плоскостями проекций.
***
Ответы
1. Предположим, что один из овалов является эллипсом. Используем известный способ нахождения фокусов эллипса: на всех овалах проводим окружности радиусом, равным большой полуоси с центрами в полюсах малой оси, точки пересечения окружностей с большими осями засекаем – это предполагаемые фокусы. Из одной из этих точек каждого овала проводим любой отрезок до пересечения с контуром овала и строим отражённый луч. Тот овал, где отражённый луч попадает в противоположный фокус, и является эллипсом. В нашем случае овал в. Эллипс – овал условно-стабильной формы. Этот термин предложен автором в связи с тем, что при изменении соотношения осей, он меняет свою конфигурацию, но не расстаётся с эллиптической формой и фокусами. Осталось два овала: стабильной и нестабильной формы. Замерив оси обоих овалов и вычислив их соотношение, замечаем, что соотношение у овала а совпадает с одноимённой константой овала стабильной формы – циклопа и равно π/2. Дополнительно убедиться в том, что это циклоп можно по другим константам. Таким образом, идентифицирован второй овал. Попытки найти фокусы на третьем овале ни к чему не приведут, поэтому можно сделать вывод – это бесфокусный овал R-0.2. Для построения многоконстантного овала циклопа достаточно размера одного (любого) элемента. Для построения эллипса достаточно знать размеры его осей. Для построения овала R-0 также нужно знать размеры осей и использовать овал циркон как график функции.
3. Все срезы батона в плоскостями общего положения будут эллиптическими, симметричными относительно двух осей. Аналогичные срезы батона а будут косыми псевдоциклопами (только центральная симметрия). Срезы батона б также будут иметь только центральную симметрию.
4. Для получения удвоенной площади все батоны нужно срезать плоскостью под углом 60 градусов к нормальному срезу. Углы с другими плоскостями проекций роли не играют.
***
Не забудьте купить сырокопчёной колбасы к праздничному столу и цветы!  Отвечайте женщинам взаимной любовью! С праздником 8 марта!
Отвечайте женщинам взаимной любовью! С праздником 8 марта!